Решение неравенств методом интервалов

Разделы: Математика, Внеклассная работа

Цели:

  1. Обобщить использование метода интервалов для решения неравенств,
  2. Показать широкие возможности этого метода для решения неравенств, содержащих переменные под знаком log, 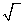, и тригонометрические функции.

Мы будем рассматривать неравенства, правая часть которых равна нулю, а левая часть представлена в виде произведения или частного функций.

Идея метода: Знак произведения или частного определяется знаком сомножителей.

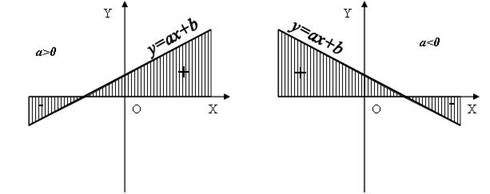
Рис.1

Линейная функция с ненулевым угловым коэффициентом меняет знак при переходе через нуль функции, причём справа от нуля знак функции совпадает со знаком углового коэффициента.

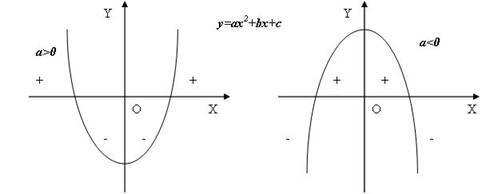
Рис.2

Квадратный трёхчлен с D>0 при переходе через каждый нуль функции меняет свой знак, причём правее большего корня знак квадратного трёхчлена совпадает со знаком его старшего коэффициента. [1]

Эти соображения приводят к следующей схеме решения неравенства:

Пример 1:[1]

  1. Найдём нули числителя: , , .
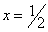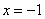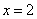  2. Найдём нули знаменателя: .
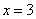  3. Наносим найденные нули на числовую ось. Т.к. неравенство строгое, то все нули изображаем выколотыми точками, которые разбивают числовую ось на интервалы:

Рис. 3

На самом правом из них знак каждого сомножителя совпадает со знаком его старшего коэффициента:

Следовательно, дробь на этом промежутке тоже отрицательна.

  1. При переходе через каждый из отмеченных нулей, один и только один из сомножителей меняет знак, и поэтому каждый раз меняется знак дроби. Учитывая это, расставляем в интервалах знаки (как показано на Рис.3).
  2. Выбираем интервалы, на которых дробь отрицательна.
  3. Записываем ответ: .

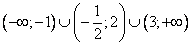В рассмотренном примере 1, знаки в промежутках знакопостоянства функции чередуются. Однако делать обобщение, что так будет происходить всегда, разумеется, не следует.

Пример 2:

  1. нули числителя:


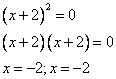
    -2 – нуль второй кратности

  2. нули знаменателя:


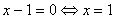
  3. наносим найденные нули на числовую ось, т.к. неравенство не строгое, то нули числителя изображаем заштрихованными точками, а нуль знаменателя мы выкалываем, т.к. это число не входит в область определения неравенства:

Рис.4

Обозначим нуль второй кратности галочкой, чтобы не забыть. Т.к. числитель всегда принимает положительные значения, то на правом крайнем промежутке знак будет зависеть от знака старшего коэффициента знаменателя, т.е. «+». Левее «1» знаменатель будет отрицательным, а числитель положительным, поэтому при переходе через число -2 знак не меняется:

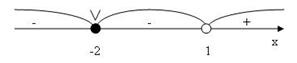
Рис.5

Это поможет понять следующая геометрическая картинка (Рис.6):

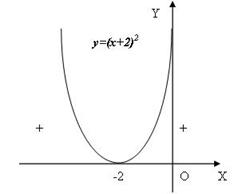
Рис.6

  1. Для записи ответа выбираем промежуток, где стоит знак «+» и заштрихованную точку 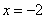, при которой дробь обращается в нуль.
    Ответ: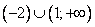

Вывод: при переходе через нуль чётной кратности, знак не меняется.

Решить по вариантам, с последующим обсуждением у доски.

I вариант

Пример 3:

  1. нули числителя:

    ;
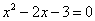
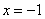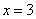
  1. нули знаменателя:

    ;
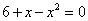
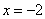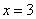
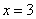    - нуль второй кратности

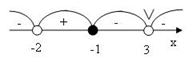
Рис.7

Ответ:

II вариант

Пример 4:

  1. нули числителя:
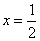    - нуль второй кратности

  2. нули знаменателя:

    ;
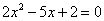
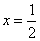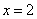
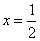    - нуль третьей кратности

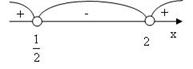
Рис.8

Ответ:

Применение метода интервалов не ограничивается решением рациональных неравенств.

Универсальность метода основана на достаточно наглядном свойстве непрерывных функций: «Если на интервале (a;b) функция f(x) непрерывна и не обращается в нуль, то на этом интервале она сохраняет знак».

Пример 5: [1] ,

Будем решать это неравенство по той же схеме, но не на всей оси, а на области определения логарифмической функции, т.е. на промежутке (*):

  1. нули числителя:

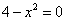
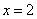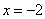    ; - не входит в (*)
  2. нули знаменателя:

    ;

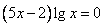
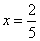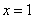
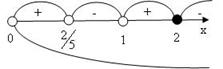
Рис. 9

  1. на самом правом промежутке
    , ,

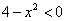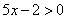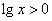
Следовательно на этом промежутке левая часть неравенства отрицательна

  1. при переходе через каждый корень меняет знак один и только один из сомножителей. Учитывая это, расставляем знаки на остальных промежутках.

Ответ: .

Пример 6:

  1. нули числителя:


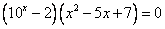
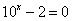
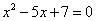
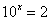
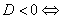    корней нет


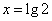
  2. нули знаменателя:
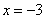
  3. решение изображаем на рис. 10:

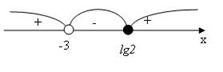
Рис.10

Квадратный трёхчлен в числителе не имеет корней и не меняет свой знак. Его знак совпадает со знаком старшего коэффициента, т.е. «+».

Ответ:.

Пример 7: ОДЗ:

Приведём неравенство к такому виду, чтобы в правой части был «0»:

  1. нули числителя:

;;;

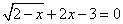
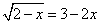
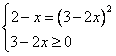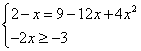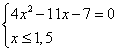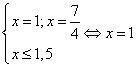
  1. нули знаменателя:
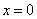
  2. решение изображаем на рис. 11:

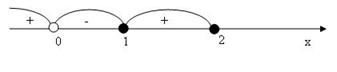
Рис.11

Ответ:.

Пример 8:

ОДЗ: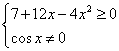

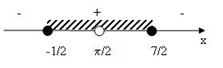
Рис.12

  1. нули числителя:
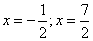
  2. нули знаменателя:

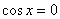
, но ОДЗ удовлетворяет только

  1. решение изображаем на рис. 13:

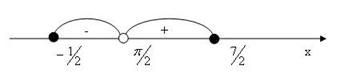
Рис.13

Ответ:.

Задание на дом: (Решение предоставлено в Приложении1)

  1. Ответ:.
  2. Ответ:.
  3. Ответ:.
  4. Ответ: .
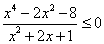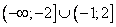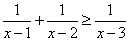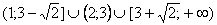
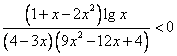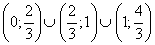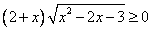  5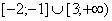. 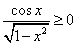Ответ:.

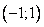Задания для факультативный занятий предоставлены в Приложении2.

Вывод: Как известно, линейная, квадратичная, степенная, показательная, логарифмическая и тригонометрические функции, а так же их композиции и функции, получаемые из них с помощью арифметических действий, непрерывны в своей области определения. Поэтому метод интервалов можно применять при решении практически всех неравенств школьного курса. Метод интервалов позволяет представить множество решений неравенства в виде объединения промежутков, границы которых либо корни соответствующего уравнения, либо граничные точки области определения.

Список литературы:

[1] "Метод интервалов" //Журнал "Квант" No12, 1985 г.