Цель урока: повторение и обобщение изученного материала путём решения комбинированных задач; развитие познавательного интереса к математике.
Задачи урока:
- совершенствовать навыки решения разнообразных задач по использованию формул арифметической и геометрической прогрессий; применять свои знания в практических ситуациях; расширять знания учащихся путём решения нестандартных задач;
- развивать математический кругозор, мышление, математическую речь;
- воспитывать стремление к непрерывному совершенствованию; воспитывать чувство прекрасного; формировать отношения взаимной ответственности при совместной работе.
Ход урока
1. Организационный момент
Сегодня у нас завершающий урок по одной из важных тем алгебры 9 класса
“Прогрессии”. Давайте сформулируем цель и задачи нашего урока. Действительно, нам предстоит обобщить и систематизировать знания по данной теме и показать применение их при решении практических задач. А также подготовиться к контрольной работе.
2. Актуализация опорных знаний
Кто желает проверить свои знания и умения, поработав с заданиями у доски? Выберите задание на лепестке ромашки. Вы уже знаете, что красный цвет лепестков ромашки говорит о том, что вас ожидает задание повышенной сложности, жёлтый цвет – задания обязательного уровня сложности, синий и зелёный – соответственно для оценок “4” и “5”. Выбирайте задания, ориентируясь на свой уровень знаний и умений.
Все остальные – приготовьтесь к устному опросу.
Вопросы к классу:
- Какую последовательность чисел называют арифметической прогрессией?
- Что показывает разность арифметической прогрессии?
- Первый член арифметической прогрессии равен 26, разность 3. Чему равен второй член данной прогрессии? Четвёртый?
- Третий член арифметической прогрессии равен 48, четвёртый равен 36. Найдите разность.
- Я задумала арифметическую прогрессию. Задайте только два вопроса, чтобы после ответа на них вы смогли бы быстро назвать седьмой член этой прогрессии.
- Дана последовательность
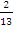 ;
; 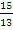 ;
; 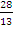 ;
; 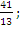
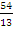 ;
; 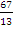 . Будет ли она арифметической
прогрессией. Обоснуйте. Найдите восьмой член
прогрессии.
. Будет ли она арифметической
прогрессией. Обоснуйте. Найдите восьмой член
прогрессии. - Какую последовательность чисел называют геометрической прогрессией?
- Что показывает знаменатель геометрической прогрессии?
- Первый член геометрической прогрессии равен 18, знаменатель равен 3. Чему равен второй член прогрессии? Третий?
- Пятый член геометрической прогрессии равен70, шестой 35. Чему равен знаменатель?
- Придумайте такую геометрическую прогрессию, чтобы ни в одном из её членов не встречалась бы цифра 1.
- Где в жизни мы встречаемся с прогрессиями?
Задания на лепестках “ромашки”:
1) Лепесток красного цвета.
Определите первый член и знаменатель геометрической прогрессии, если известно, что разность между её четвёртым членом и вторым равна 18, а разность между пятым и третьим членами равна 36.
2) Лепесток синего цвета.
Найдите сумму бесконечной геометрической
прогрессии: b(n)![]() ; 3;
; 3; ![]() …
…
3) Лепесток зелёного цвета.
Найдите сумму двенадцати членов арифметической прогрессии, если первый член прогрессии равен – 5, а разность равна 3.
4) Лепесток жёлтого цвета.
Между числами 2 и 22 вставьте четыре числа так, чтобы вместе с данными числами они составили арифметическую прогрессию.
3. Закрепление изучаемого материала
А теперь проверим наши знания в тестовых заданиях. Перед вами бланки вопросами и листочки, которые подпишите и пронумеруйте от 1 до 5. Выберите из ответов на вопрос номер правильного ответа.
Вариант 1.
1. Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго равен
- предыдущему, умноженному на одно и то же число;
- предыдущему, сложенному с последующим;
- предыдущему, увеличенному в одно и то же число раз;
- предыдущему, сложенному с одним и тем же числом.
2. Последовательность (an) - арифметическая прогрессия. Найдите а5, если а1=10, d=4.
- 26;
- 30;
- 256;
- 304.
3. Запишите формулу суммы n- первых членов арифметической прогрессии
- Sn=
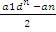 ;
; 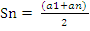 ;
; 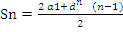 ;
; 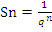
4. Что показывает знаменатель геометрической прогрессии?
- на сколько последующий член прогрессии меньше предыдущего;
- во сколько раз последующий член прогрессии больше (меньше) предыдущего;
- разность между каждым последующим членом прогрессии.
5. Запишите формулу суммы геометрической прогрессии:
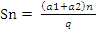 ;
; - Sn=
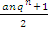 ;
; 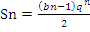 ;
; 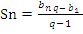
Вариант 2.
1. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго равен
- второму, увеличенному в n раз;
- предыдущему, сложенному с одним и тем же числом.
- предыдущему, умноженному на одно и то же число;
- последующему члену прогрессии, умноженному на предыдущий.
2. Последовательность (Сn ) – арифметическая прогрессия. Найдите С1, если C30 =128? d= 4.
- 8;
- 12;
- 0, 5;
- 16.
3. Запишите формулу знаменателя геометрической прогрессии:
- q=
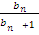 ;
; - q=
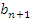 -
-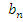 ;
; - q=
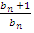 ;
; - q=
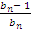 .
.
4. Найдите сумму бесконечной геометрической
прогрессии (![]() ):
9; 3; 1….
):
9; 3; 1….
- 13, 5;
- 27;
- 51, 5;
- 4, 5.
5. Запишите формулу n-го члена арифметической прогрессии:
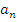 =
=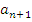 +d (n – 1);
+d (n – 1); 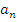 =
=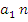 (
(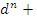 1);
1); 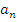 =
=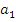 +d (n – 1);
+d (n – 1); 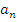 =
=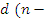 1).
1).
Ответы:
1 вариант: 41224.
2 вариант: 32313.
Наша дальнейшая работа будет строиться так: четыре группы по 2 человека будут разгадывать кроссворд. Разгадка зашифрованных слов даст ответ на вопрос, что нужно, чтобы успешно справиться с любым делом. А все остальные пишут самостоятельную работу по вариантам.
Задание 1. Найдите сумму бесконечной геометрической прогрессии.
Вариант 1 (![]() ):
49; 7; 1 …
):
49; 7; 1 …
Вариант 2 (![]() ); 0,
4; -0, 04; 0,004…
); 0,
4; -0, 04; 0,004…
Вариант 3 (![]() );
); ![]() ; 1;
; 1; ![]() .
.
Вариант 4 (![]() );
); ![]() ;
; ![]() ;
; ![]()
Задание 2. Найдите первый член бесконечной геометрической прогрессии по известной её сумме S и знаменателю q.
Вариант 1 S=16, q=![]()
Вариант 2 S=81, q=![]()
Вариант 3 S=4![]() + 4; q=
+ 4; q=![]()
Вариант 4 S=3![]() - 1); q=
- 1); q=![]()
Задание 3. Представьте в виде обыкновенной дроби число:
Вариант 1 0, (7)
Вариант 2 0, (28)
Вариант 3 2, (13)
Вариант 4 0, 5(14)
Кроссворд
| Я | В | Ь | А | Б | П | Е | О | Р | К | С |
| -15 | -1,3 | 180 | - |
26 | 1, 5 | - 7 | 104 | 3 | 2 |
Арифметическая прогрессия:
- a1=10, d=4, a5 - ?
- a2=2, a1=9, d - ?
- a5= - 3, 7; d= - 0,6, a1 - ?
- c5=27, c27=60, d - ?
- (an): - 16; - 13… S16 - ?
- a1=4; d=2; S12 - ?
Геометрическая прогрессия
- b1=2, 6; q= - 0, 5; b2 - ?
- x1=16; q= 0,5; x4 - ?
- b1=24; b2=36; q - ?
- b5=
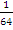 ; q=
; q=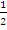 ; b1 - ?
; b1 - ? - a1=3; q= -2; S4 - ?
4. Подведение итогов урока.
5. Домашнее задание: № 440 (а), 451 (в).