В начальном курсе математики особое место отводится простым (опорным) задачам. Умение решать такие задачи – фундамент, на котором строится работа с более сложными задачами. Обучение учащихся составлению текстовых задач тесно переплетается с умением решать задачи. Уже с 1-го класса по программе ОС «Школа 2100» вводится раздел «Задачи». Сначала, на подготовительном этапе, учитель с детьми выполняют задания такого рода: восстановление развития сюжета по серии рисунков; составление различных рассказов математического содержания к одному сюжетному рисунку; завершение серии рисунков до полного восстановления сюжета. Третий вид заданий по существу является прямым подходом к понятию задачи, т.к. ставит учеников в ситуацию наглядного изображения двух данных и поиска (выбора) соответствующего им искомого.
На следующих этапах идёт обучение первоклассников умению работать с текстом задачи, знакомство с понятиями: задача, условие задачи, вопрос задачи, схема задачи, выражение, решение задачи, ответ задачи через такие мыслительные операции, как сравнение, анализ, синтез.
Следующий шаг – обучение схематическому изображению данного и искомого, затем – работа над составлением выражения к вопросу через вопрос: «А что мы ищем: целое или часть?».
Используя правило о нахождении целого и части, дети выбирают действие (сложение или вычитание), составляют выражение, находят его значение, что и есть решение задачи, затем называют ответ задачи.
Параллельно обучению решению задач, уже в 1-м классе детям можно предлагать задания, которые формируют и развивают все виды познавательные УУД, например такие: придумай задачу по схеме; составь задачу по выражению; составь математический рассказ по схеме и выражению.
Возможно, детям предлагать решать задачи, в которых нет вопроса или недостаточно данных, что приводит детей к проблеме.
В процессе составления учащимися текстовых задач по математической или вспомогательной модели нередко возникают затруднения. Скорее всего, это обусловлено тем, что не предлагается механизм работы над данным видом деятельности. Научить составлять текстовые задачи младших школьников – это значит научить излагать и воспроизводить структуру высказывательной модели задачи, опираясь на взаимосвязь каждого этапа работы. Под структурой подразумеваются не составные части (условие и требование), а процесс составления задачи с учётом последовательного выполнения действий.
Главная цель этого вида деятельности – сформировать умение строить высказывательную модель задачи. Для того чтобы добиться результативности в работе, педагог старается предусмотреть в методике обучения составлению текстовых задач такие этапы как сюжет, объекты, количественные характеристики, требование, текст задачи.
Научить составлять текстовые задачи младших школьников – это значит научить излагать и воспроизводить структуру высказывательной модели задачи, опираясь на взаимосвязь каждого этапа работы.
Под структурой подразумеваются не составные части (условие и требование), а процесс составления задачи с учётом последовательного выполнения действий. Главная цель этого вида деятельности – сформировать универсальное учебное действие – словесное моделирование математических задач. Для того чтобы добиться результативности в работе, учитель должен предусмотреть в методике обучения составлению текстовых задач следующие этапы: сюжет, объекты, количественные характеристики, требование, текст задачи.
Под сюжетом мы подразумеваем действия, производимые с предметами. Для того чтобы задачи были разнообразные по содержанию, необходим набор слов, которые дети использовали бы при составлении задач. Например:
| подарили заплатили убрали начертили полили |
вылепили отрезали вырастили принесли уехали |
покрасили погрузили прочитали разложили и т.д. |
Для нахождения объектов к выбранному сюжету можно использовать следующие тренировочные упражнения, которые нравятся детям, развивают их словарный запас, фантазию.
1. Перечислите предметы, которые можно подарить (убрать, разложить и т.д.).
2. Выберите объекты, которые могут соответствовать данному сюжету. Найдите «лишнее» слово.
|
|
Для составления задачи с опорой на математическую или вспомогательную модель можно ориентироваться на следующий алгоритм.
Алгоритм обучения составлению текстовых задач.
- Придумай сюжет задачи.
- Назовите объекты, о которых будет говориться в задаче.
- Дай количественную характеристику объектам.
- Сформулируй требование задачи.
- Смоделируй текст задачи.
Например: необходимо составить текстовую задачу, опираясь на выражение: 3 • 2 + 2 • 5
- Придумаю сюжет задачи: покупка школьных принадлежностей.
- Назову объекты, о которых будет говориться в задаче: ученик, тетради, ручки.
- Дам количественную характеристику объектам: данная задача будет на зависимость величин: цена, количество, стоимость.
Разъясню записи:
А) 3 • 2 Второй множитель указывает на количество предметов. Предположим, что это ручки, значит, купили 2 ручки по 3 рубля.
Б) 2 • 5 Купили 5 тетрадей по 2 рубля.
4. Сформулирую требование задачи.
Два произведения соединены знаком «+», следовательно, последнее действие будет сложение. Результаты произведений – это стоимости. Значит, требование можно сформулировать следующим образом: «Найти стоимость всей покупки» или «Сколько уплатили за всю покупку?».
5. Смоделирую текст задачи:
«Ученик купил 2 ручки по 3 рубля и 5 тетрадей по 2 рубля. Сколько ученик заплатил за всю покупку?»
Предлагаем рассмотреть приемы словесного моделирования.
Этот приём основан на вспомогательной модели с опорой на один и тот же сюжет, объекты.
Чтобы организовать поиск при составлении задачи, первоначально необходимо придумать «сюжет», т.е. достаточно найти какое-либо ключевое слово, характеризующее действие над предметами. Примерами могут служить различные слова: строить, решать, росло, улетело и т.д.
Для завершения смысла «сюжета» добавляем к содержанию объекты. Например, решать можно примеры, уравнения, задачи и т.п.
Если это необходимо, то следует ввести действующих лиц: ими могут быть мама, ученик и т.д.
На следующем этапе дети дополняют объекты количественными и качественными характеристиками, включая различные отношения.
В завершение формулируют «требования», которые можно начать со слов: «Сколько…», «Найти…», «На сколько…», «Во сколько…».
На основе выбранного сюжета, объектов и их количественных характеристик, а также требований, моделируется текст задачи.
В ходе беседы с учащимися можно составить и использовать различную структуру модели для организации поиска и планирования задачи на естественном языке, которая может предполагать разновариантные способы формирования текста. Например:
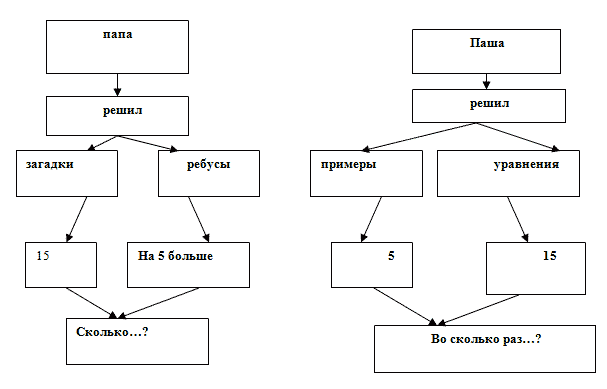
Опираясь на данный план и комбинируя различные сюжеты, объекты, количественные характеристики, отношения, требования, можно составить большое количество задач. На этапе подготовки можно установить соотношения между ключевым словом сюжета и объектами, между действующим лицом и ключевым словом и т.д.
Можно продолжить поиск моделирования задачи, используя различные интерпретации схем.
В последующем предлагаемые детьми для составления задач сюжеты, объекты, количественные и качественные характеристики, отношения, требования можно не фиксировать на доске, а в ходе моделирования использовать алгоритм, описанный выше.
Таким образом, смысл термина «составление задачи» обозначает разные понятия:
1.результат, т.е. словесная модель;
2.процесс составления задачи, приводящий к
формулированию текста в ходе последовательного
выполнения действий, применяемых в приёме.
Второй приём основан на предложенных объектах, сюжете, вспомогательной модели.
| ШКОЛЬНИКИ СВЕКЛА ВЫРАСТИЛИ МОРКОВЬ ОВОЩИ КАРТОФЕЛЬ |
|
Необходимо предложить детям выбрать
слова, которые охарактеризуют сюжет задачи. (Школьники
вырастили овощи.)
Далее идёт беседа по содержанию:
– Где выращивают школьники овощи? (На
пришкольном участке.)
– Какое слово из предложенных объектов,
записанных в столбце, общее? (Овощи.)
– Какие овощи вырастили дети? (Свёклу, морковь,
картофель.)
Затем предлагается соотнести предложенные
объекты со схемой, указав количественные
характеристики. (Целое – овощи. Целое
неизвестно. Части – свекла – 20 кг, морковь – 12 кг,
картофель – 8 кг).
А сейчас сформулируем текст задачи. (Школьники
вырастили на пришкольном участке 20 кг свёклы, 12
кг моркови, 8 кг картофеля. Сколько кг овощей
вырастили школьники?)
Можно спросить ребят, о какой величине говорится
в задаче? (О массе.)
Потом попросить детей сформулировать требование
иначе. (Какова масса собранного урожая?)
Третий приём составления задач основан на готовых задачах, содержащих один сюжет и часть общих объектов с их количественными характеристиками.
| Задача 1. В школьную
библиотеку привезли учебники. В первый день
библиотекари расставили 210 учебников по русскому
языку, во второй день – 135 учебников по
математике. Сколько учебников расставили
библиотекари по полкам за два дня? Задача 2. В школьную библиотеку привезли учебники. В первый день библиотекари расставили по полкам 210 учебников по русскому языку, во второй день – 63 учебника по чтению. Сколько учебников расставили библиотекари по полкам за два дня? Задача 3. В школьную библиотеку привезли учебники. В первый день библиотекари расставили по полкам 97 учебников по английскому языку, во второй день – 63 учебника по чтению. Сколько учебников расставили библиотекари по полкам за два дня? |
Попросить детей внимательно прочитать задачи, найти общее (Сюжет, требование.) Дальше идёт беседа:
– Что можно сказать об объектах и
количественных характеристиках задач? (Часть
объектов и их количественные характеристики в
первой и второй задачах; во второй и третьей
задачах одинаковые).
Затем дети формулируют текст задачи, используя
все объекты и их количественные характеристики. (В
школьную библиотеку привезли новые учебники. Из
них в первый день расставили по полкам 210
учебников по русскому языку и 97 по английскому
языку, во второй – 135 учебников по математике и 63
учебника по чтению. Сколько учебников расставили
библиотекари по полкам за два дня?)
Четвертый приём составления задач основан на предложенном решении с подробным пояснением.
| 3 + 15 = 18 – концертов дал детский хор вгороде и
санатории. 30 – 18 = 12 – концертов дал детский хор в сельских клубах. |
Дети внимательно рассматривают решение с пояснениями, затем отвечают на серию вопросов:
– Известно ли нам, где давал детский хор
концерты? (В городе, санатории, сельских клубах).
– Известно ли нам, сколько концертов дал хор в
городе? (3 или 15)
– Известно ли нам, сколько концертов дал хор в
санатории? (15 или 3)
– Сколько всего концертов дал хор? (30)
– Составьте задачу по первому равенству. (Детский
хор дал 3 концерта в городе и 15 концертов в
санатории. Сколько всего концертов дал детский
хор в городе и санатории?)
– Составьте задачу по второму равенству. (За
лето детский хор дал 30 концертов. Из них 18 – в
городе и санатории, а остальные в сельских
клубах. Сколько концертов дал детский хор в
сельских клубах?)
– Опираясь на решение задачи, сформулируйте
требование.
– Сформулируйте текст задачи, опираясь на два
действия. (Детский хор дал 30 концертов. Из них 3
– в городе, 15 – в санатории, а остальные – в
сельских клубах. Сколько концертов дал детский
хор в сельских клубах?)
5 прием «Кластер».
Изучив технологию развития критического мышления на основе чтения и письма, ее методический прием «Кластер», возможно смоделировать следующую работу над задачей.
Детям предлагается, работая в группе, либо в паре, заполнить кластер – это графические систематизаторы, которые показывают несколько различных типов связей между объектами или явлениями. В центре листа пишется слово (тема, проблема). В данном случае – ключевое слово «задача». Далее вокруг этого слова дети, обсуждая, выбирают и наклеивают элементы задачи (условие, вопрос, схема, выражение, решение, ответ задачи). Для «ловушки» можно группе предложить 1-2 лишних понятия (например: тема, идея). Этот этап одинаково выполняют все группы класса. Обязательно нужно проверить правильность выполнения этого этапа работы. А вот далее каждая группа получает сюжетную картинку, на основе которой они должны составить задачу, вписывая в кластер условие задачи под условием, вопрос под вопросом, схему под схемой и т.д. На первых порах в 1 классе можно вместе с сюжетной картинкой выдавать и набор карточек с разными условиями, вопросами, выражениями задач. Дети должны выбрать необходимые, наклеить или вписать в кластер.
Кроме этого, педагоги из личного опыта
замечают, насколько интересней и живее проходит
урок математики, если на нём рассматривается
материал, связанный с историей родного края.
Необходимость его использования в процессе
обучения младших школьников решению и
составлению задач совершенно очевидна. Умелое
использование краеведческого материала
облегчает задачу обучения, т.к. вызывает у
учеников несомненный интерес. Учителя нечасто
применяют этот приём не потому, что не понимают
его роль и значение, а потому, что порою трудно
найти нужный материал, выбрать из него наиболее
важное и интересное. Вот здесь и надо дать
возможность детям проявить творчество, смекалку
в умении сбора необходимой информации.
Например, используя только два факта: город Пермь
основан в 1723 году, а город Кунгур в 1648 году –
можно составить сразу несколько текстовых задач.
(Город Пермь основан в 1723 году, а город Кунгур в 1648
году. Какой город старше и на сколько лет? Какой
город моложе и на сколько лет? Сколько лет было
городу Пермь в 1998 году, в 2006 году? и т.д.).
Нетрудно представить, насколько оживится деятельность учащихся, если предложить им самим задать вопросы к этим условиям, тем более, если дать им возможность подбирать интересные факты, на основе которых на уроке будет организована работа.
Как часто дети могут назвать реки, горы, представителей флоры и фауны своего родного края? Вот ещё одно направление их поиска. Большим подспорьем в поиске числового материала о родном крае может стать учебное пособие Н.А.Князевой «Маленький пермяк». Можно сказать, что учитель одновременно «убивает двух зайцев»: с одной стороны, расширяет представления учащихся о родном крае, формирует патриотизм и воспитывает любовь к малой Родине, с другой стороны делает процесс обучения творческим, что, несомненно, положительно сказывается на формировании познавательных УУД. С ранних лет ребёнок учится добывать знания самостоятельно из разных источников – газет, журналов, книг, справочников, энциклопедий, телевизионных передач, из рассказов бабушек и родных, на экскурсиях в музеи, по городу, на предприятия, что является одной из важнейших задач современной системы образования.
Упражнения по составлению и преобразованию задач помогают обобщению знаний о связях между данными и искомыми, так как дети при этом исследуют, что можно узнать по определённым данным. Очень важно учить ребёнка сразу на реальных количественных отношениях. Если он, к примеру, едет из г.Перми в г.Краснокамск, то он легко сопоставит расстояние до других населенных пунктов.
Всегда педагог радуется тому, что ученики смогли самостоятельно добыть информацию, составить с помощью неё текстовую задачу. Детям очень нравятся моменты на уроках математики, когда-либо учитель, либо ребёнок зачитывает свою задачу, которую предлагает решить коллективу класса. Этой работе можно отводить примерно 10 минут 1-2 раза в неделю на уроках математики. На первых порах можно предлагать детям решить задачи, которые составил учитель, сопровождая интересным рассказом, о том объекте, о котором шла речь в данной задаче, показом слайдов, фотографий. Детям это понравится, вот здесь и можно предложить им попробовать самостоятельно составить задачи краеведческой направленности, ведь с различными приёмами составления задач, с алгоритмом составления задач они уже знакомы. Результатом плодотворной работы учащихся, педагога станет альбом-задачник, содержащий составленные задачи краеведческой направленности.
Такая целенаправленная работа, проводимая систематически, позволяет снять некоторый психологический барьер – та информация, которую ученики получают на уроках, добывают сами, используется на уроке; им разрешено творить, расширяется их кругозор и появляется потребность самостоятельно добывать знания, то есть учить себя учиться. Речь идет о формировании всех групп УУД, в том числе и познавательных:
– поиск и выделение необходимой
информации, применение методов информационного
поиска, в том числе с помощью компьютерных
средств для составления и решения задач;
– структурирование знаний по разделу «Задачи»;
– осознанное и произвольное построение
грамотного речевого высказывания в устной и
письменной форме при составлении и решении
задач;
– усвоение смысла арифметических действий,
связь между компонентами и результатами
действий, зависимость между величинами при
составлении задач;
– действовать по заданному плану, алгоритму с
целью создания текстовой задачи;
– составлять задачи по вспомогательным и
готовым моделям;
– объяснять (пояснять) ход решения задачи;
– обнаруживать и устранять ошибки логического (в
ходе составления и решения задач) и
арифметического (в вычислении) характера;
– наблюдать за изменением решения задачи при
изменении её условия, вопроса;
– самостоятельно выбирать способ решения задачи;
– кодирование/замещение (использование знаков и
символов как условных заместителей реальных
объектов и предметов);
– декодирование/считывание информации;
– умение использовать наглядные модели (схемы,
чертежи, планы), отражающие пространственное
расположение предметов или отношения между
предметами или их частями для решения задач;
– умение строить схемы, модели и т.п.