Урок алгебры и начала анализа «Числовые последовательности и способы их задания». 10-й класс

Цели урока:

- вспомнить что такое последовательность;
- изучение способов задания числовых последовательностей;
- развитие устных вычислительных навыков, математической речи учащихся, формирование аналитических и логических способностей, расширение кругозора;
- воспитание самостоятельности, интереса и уважения к изучаемому предмету.

3. Числовые последовательности и способы их задания.

В 9 классе на уроках алгебры мы уже встречались с понятием числовой последовательности. Рассматривали свойства некоторых последовательностей, способы их задания. Арифметическая и геометрическая прогрессии нами были изучены более подробно. Мы познакомились с формулами n-го члена прогрессии, суммы n первых членов прогрессии.

• Рассмотрим ряд натуральных чисел N:
• 1,  2,  3, …,  n – 1,  n, п + 1, …
• Функцию y = f(x), x 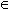N называют функцией натурального аргумента или числовой последовательностью и обозначают y = f(n) или  y1,  y2, …, yn, … или {уn}.
• Величина уn называется общим членом последовательности.

Обычно числовая последовательность задаётся некоторой формулой уn = f(n), позволяющей найти любой член последовательности по его номеру n; эта формула называется формулой общего члена.

• Перечислением членов последовательности (словесно).

Последовательность простых чисел: 2; 3; 5; 7; 11; 13; 17; 19; 23; 29; …

• Заданием аналитической формулы.

Арифметическая прогрессия: a_n = a₁ + (n – 1)d

• Заданием рекуррентной формулы.

Геометрическая прогрессия: b_{n + 1} = b_n • q

Слайд 4–6. Заполнить таблицу по заданным формулам. (Учащиеся заполняют таблицы в тетрадях)

Слайд 7. Рассмотрим примеры числовых последовательностей:

1,  2,  3,  4,  5, … –  ряд натуральных чисел;

2,  4,  6,  8,  10, … – ряд чётных чисел;

1, 8, 27, 64, 125, … – ряд кубов натуральных чисел;

5, 10, 15, 20, … – ряд натуральных чисел, кратных 5;

1, 1/2, 1/3, 1/4, 1/5, ... – ряд вида 1/n, где n N; и т.д.

Слайд 8–12

Учащиеся устно решают разноуровневые задачи на определение последовательностей.

4. Свойства числовых последовательностей. Слайд 13–15

• Ограниченность числовой последовательности.
• Возрастание и убывание числовой последовательности.

5.  Подведение итогов урока.

Приложение