Форма проведения: урок закрепления и повторения знаний
Цель: обобщить и проверить теоретические и практические знания учащихся по данной теме.
Задачи:
- Образовательные: продолжить формирование навыков выполнения действий с функциями; систематизировать и обобщить знаний по теме; проконтролировать степень усвоения знаний, умений и навыков по теме;
- Развивающие: развивать логическое мышление, учить анализировать, обобщать; продолжить работу по развитию математической речи и памяти обучающихся;
- Воспитательные: развитие сотрудничества при работе в парах; приучать к умению общаться и выслушивать других; воспитание сознательной дисциплины.
Технические средства обучения:
- компьютер для учителя, проектор, экран;
- ноутбуки для каждого обучающегося.
ХОД УРОКА
1. Организационный момент. Учитель здоровается с детьми, отмечает готовность класса к уроку.
– Прочитайте эпиграф к уроку
Пусть математика сложна,
Ее до края не познать,
Откроет двери всем она,
В них надо только постучать.
– В чем суть строк?
– Кому автор посвящает слова?
– Давай приоткроем дверь такой сложной и
интересной науки, как математика. Ведь каждому из
вас предстоит показать свои знания на
обязательном экзамене по математике. Сегодня на
уроке повторим умения выполнять действия с
функциями, это задачи В9.
2. Актуализация теоретических знаний
Самостоятельная работа с фронтальной проверкой.
– Без знания некоторых теоритических сведений переход к решению задач невозможен. Поработаем с карточками №1.
| Карточка №1 Впишите пропущенные слова 1. Геометрический смысл производной состоит в
том, что значение __________________ функции f(x) в
т.x |
3. Актуализация практических знаний. Фронтальная работа с чертежом на доске.
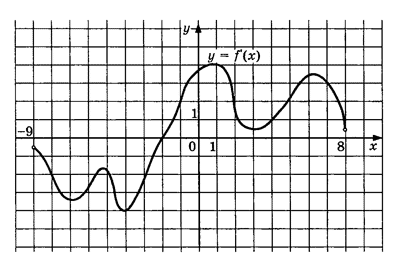
Рисунок 1
Вопросы:
- Найдите промежутки возрастания функции f(x).
- Найдите промежутки убывания функции f(x).
- Посчитайте количество точек экстремума функции f(x).
- Назовите точки максимума и минимума функции f(x).
Теперь сотрем знак ‘ в производной и ответим на те же вопросы.
4. Решение задач. Презентация. Каждый обучающийся выбирает вопрос и дает ответ на него. (Приложение 1)
5. Физкультминутка под музыку
1) Исходное положение – сидя на стуле. Плавно
наклонить голову назад, вперед, не поднимая плеч.
4-6 раз.
2) Исходное положение – сидя на стуле, руки – на
поясе. Поворот головы вправо. Исходное положение.
Поворот головы влево. Исходное положение. 4-6 раз.
3) Исходное положение – сидя на стуле, руки – на
поясе.
Взмахом левую руку занести через правое плечо. Голову повернуть влево. Затем наоборот. 4 раза.
6. Математическое лото. Работа в парах.
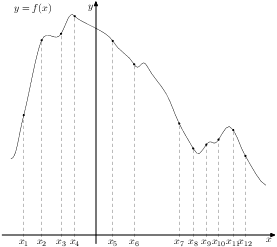
| На рисунке изображён график функции y
= f(x) и двенадцать точек на оси абсцисс: x1, x2, x3, ..., x12. В скольких из этих точек производная функции f(x) отрицательна?
Рисунок 2 |
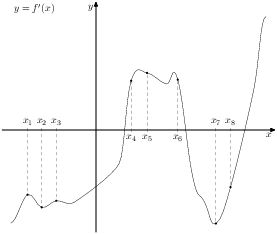
На рисунке изображён график
производной функции y = f'(x) и восемь точек на оси абсцисс: x1, x2, x3, ..., x8. В скольких из этих точек функция f(x) возрастает?
Рисунок 3 |
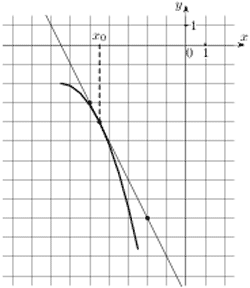
| На рисунке изображены график функции
y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рисунок 4 |
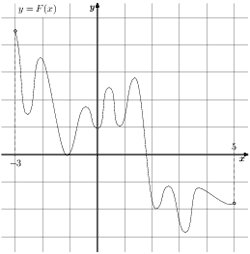
На рисунке изображён график функции y
= F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (– 3;5). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [– 2; 4]
Рисунок 5 |
Подберите правильные ответы.
Ответы:
| 7 | 3 |
| – 2 | 10 |
7. Проверочный тест (Приложение 2)
8. Подведение итогов. Давайте подведем итоги уроки. А помогут вам такие слова:
Сегодня я узнал…
Было интересно…
Было трудно…
Я понял, что…
Теперь я могу…
У меня получилось…
Я попробую…
Мне захотелось …
– Спасибо вам за урок. Надеюсь, вы справитесь с заданиями на экзамене.
Используемая литература:
- Мартышова Л.И. Открытые уроки алгебры и начал анализа: 9-11 классы. – М.: ВАКО, 2012. – 272 с.
- Семёнов А.Л. ЕГЭ: 3000 задач с ответами по математике. Все задания группы В. – М.: Издательство «Экзамен», 2012. – 543 с.
Интернет-ресурсы