В классах с углубленным изучением математики часто практикуются решение задач на выяснение расположения корней квадратного трёхчлена. В общеобразовательных классах эта тема изучается на элективных курсах. Ниже предлагается описание моего опыта работы по данной теме в 11 классе на занятиях элективного курса «Решение задач с параметрами». Используются два способа: свойства квадратного трёхчлена и применение геометрического смысла производной.
Изучение нового материала.
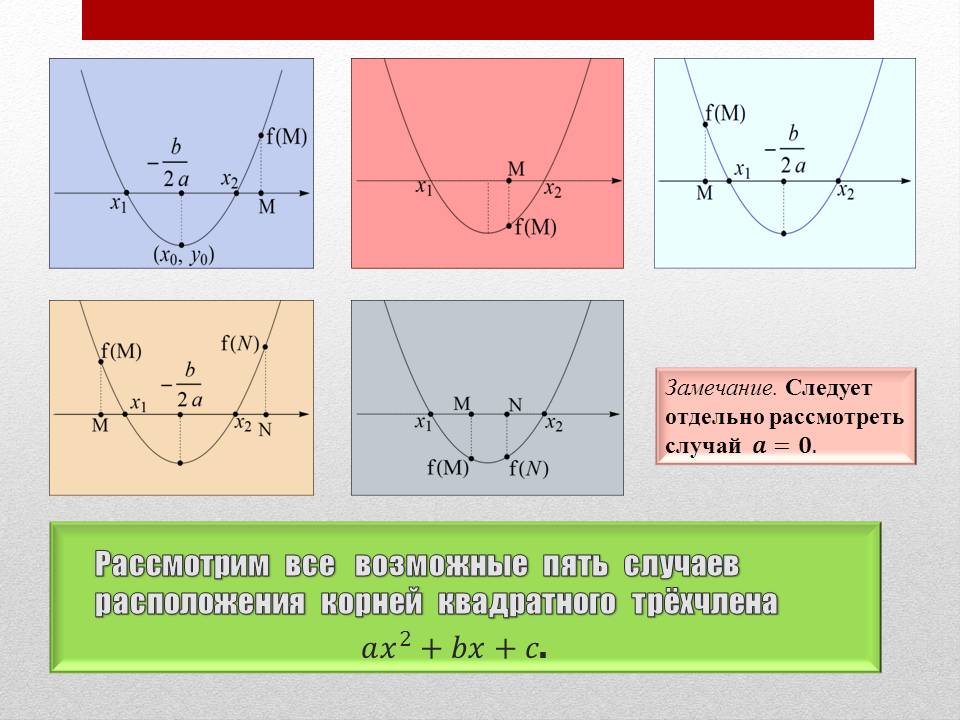
Теоретическая часть материала разбирается с помощью презентации. Рассмотрим все возможные пять случаев расположения корней квадратного трёхчлена.
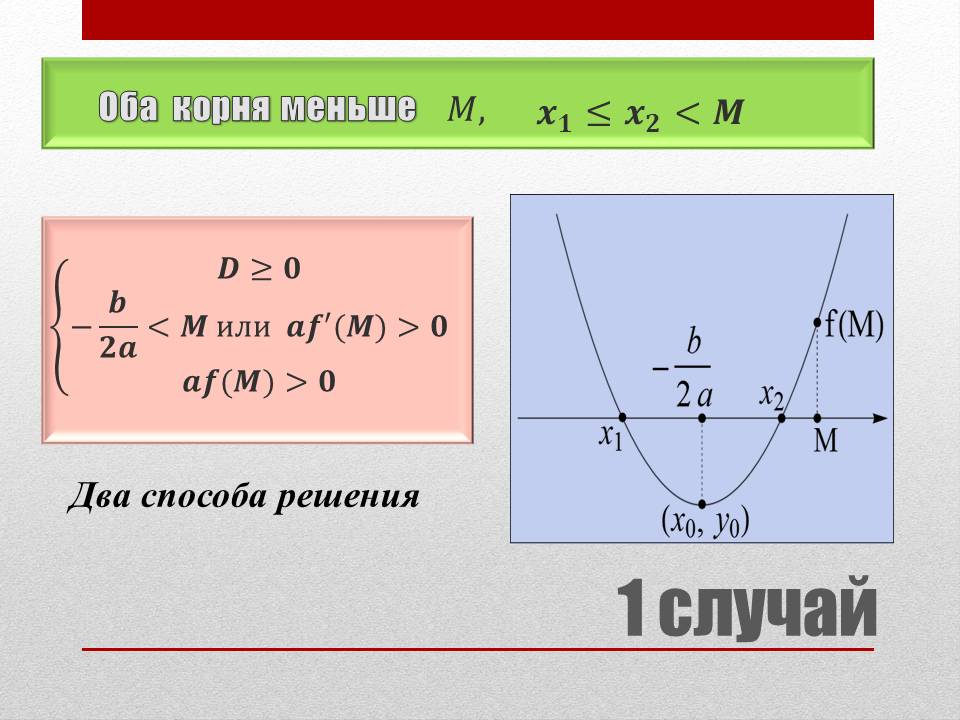
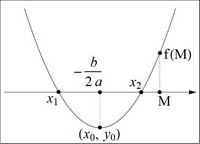 1 случай: оба корня меньше M,
1 случай: оба корня меньше M,
т.е. x1 ≤ x2 < M (Рисунок 1)
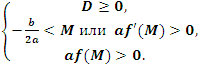
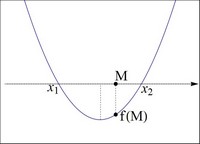 2 случай: один корень меньше,
2 случай: один корень меньше,
а другой больше M, т.е. x1 < M < x2 (Рисунок 2)
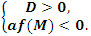
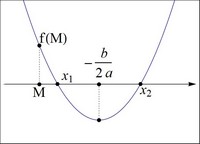 3 случай: оба корня больше M,
3 случай: оба корня больше M,
т.е. M < x1 ≤ x2 (Рисунок 3)
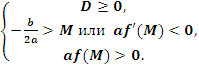
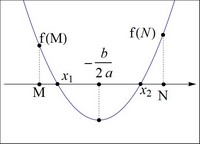 4 случай: оба корня внутри интервала (M;N),
4 случай: оба корня внутри интервала (M;N),
т.е. M < x1 ≤ x2 < N (Рисунок 4)
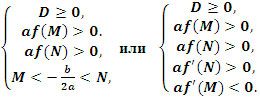
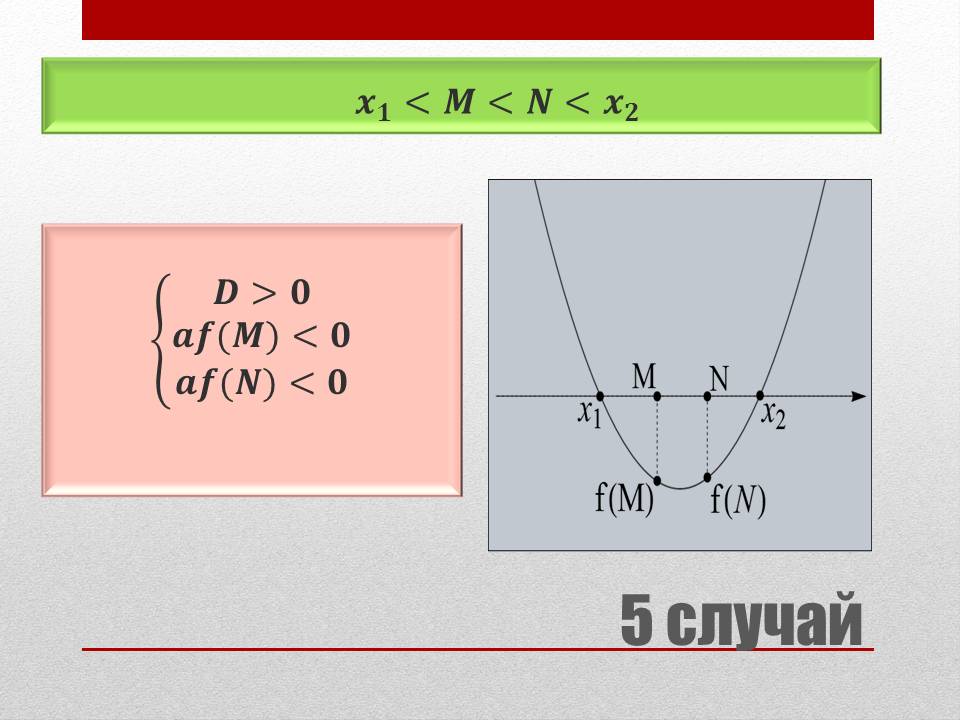
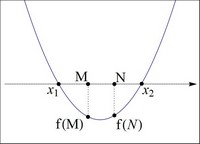 5 случай: x1 < M < N < x2 (Рисунок 5)
5 случай: x1 < M < N < x2 (Рисунок 5)
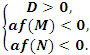
Замечание. Следует особо рассмотреть случай a = 0.
Упражнения для закрепления
Рассмотрим примеры применения рассмотренного учебного материала. Используем два способа решения: свойства квадратного трёхчлена и применение геометрического смысла производной. Учащимся выдаются таблицы (Приложение 1). Задания №1, №2, №4 выполняют ученики на доске. Задания № 3, №5 выполняют самостоятельно (проверка решений с помощью презентации).
№1. Найти значения a, при которых корни x1, x2 уравнения
2x2 - 2(2a + 1)x + a(a - 1) = 0 удовлетворяют условиям x1 < a < x2.
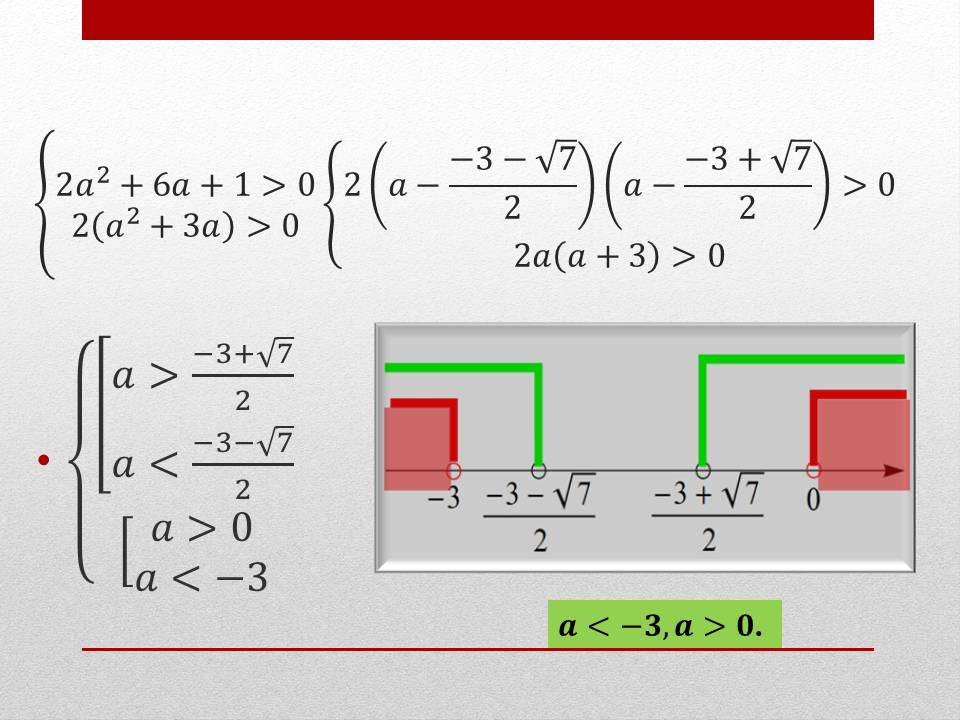
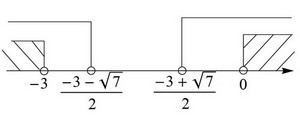 Решение. Используем второй случай. Составим систему неравенств.
Решение. Используем второй случай. Составим систему неравенств.
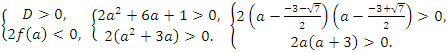
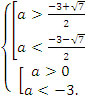
Ответ: a < -3, a > 0.
(Рисунок 6)
№2. Найти все действительные a, при которых корни оба корня уравнения
(2a + 3)x2 + (a + 1)x + 4 = 0 заключены между -2 и 0, т.е. -2 < x1 ≤ x2 < 0.
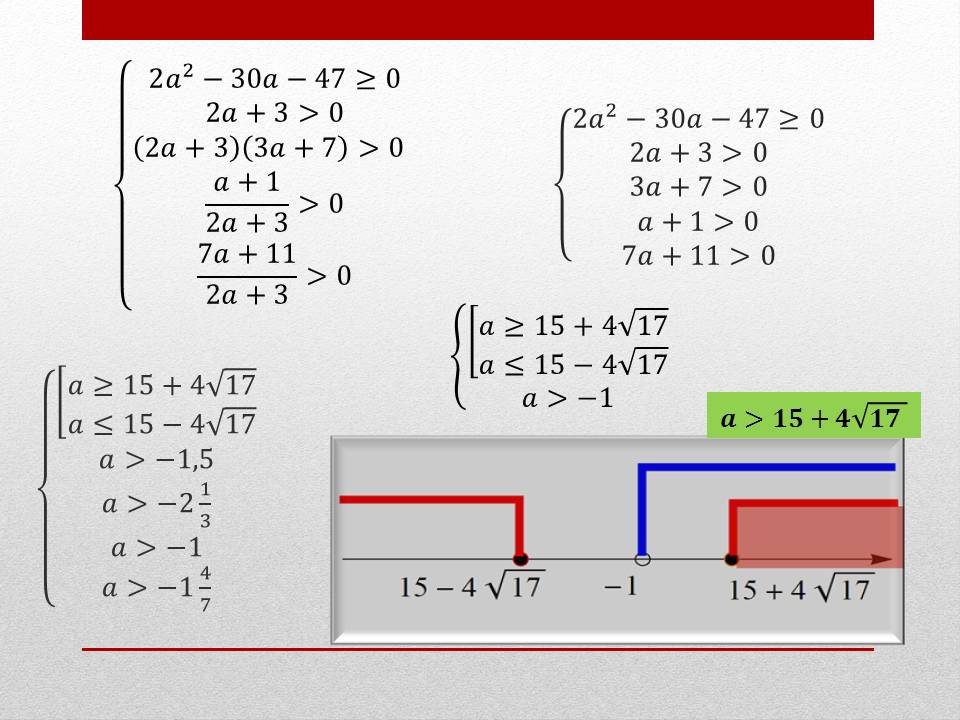
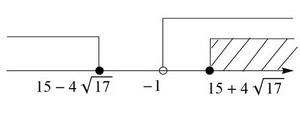 Решение. Имеем четвёртый случай. Составим систему неравенств.
Решение. Имеем четвёртый случай. Составим систему неравенств.
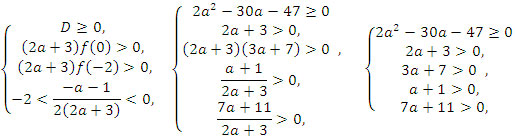
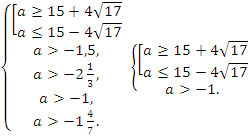
Ответ: a > 15 + 4√17. (Рисунок 7)
№3. При каких a корни x1, x2 уравнения (a -2)x2 - 2(a + 3)x + 4a = 0 удовлетворяют условию x1 < 2 < 3 < x2 ?
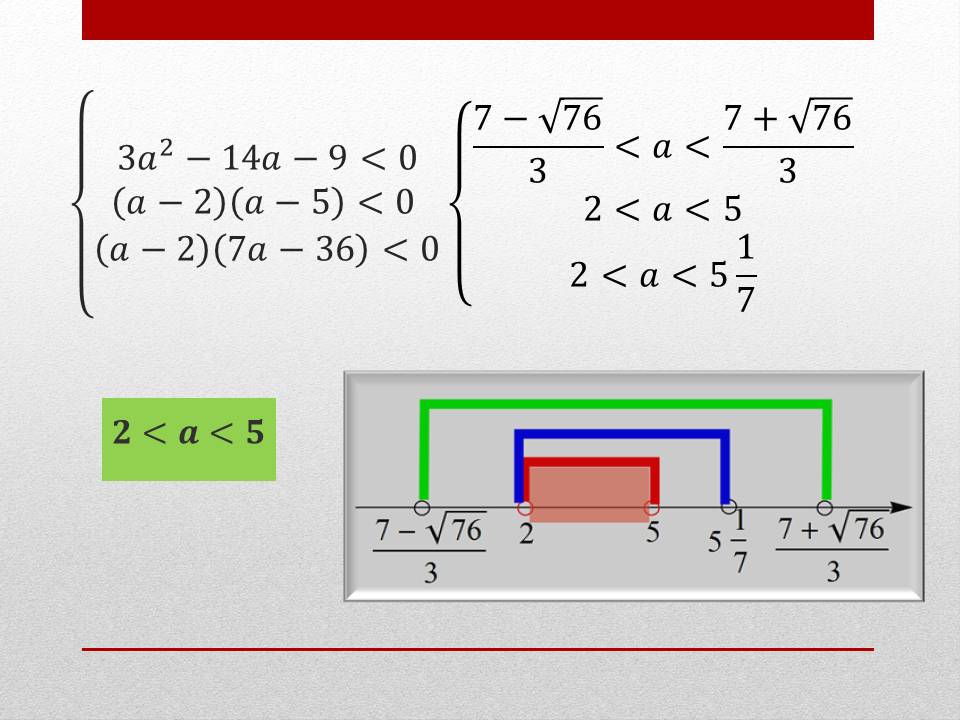
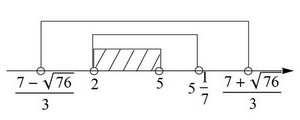 Решение. Имеем пятый случай.
Решение. Имеем пятый случай.
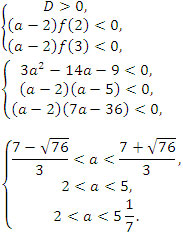
Ответ: 2 < a < 5 (Рисунок 8)
№4. При каких a корни уравнения ax2 - 2(2a - 1)x + 2 - 3a = 0
удовлетворяют условию x1 > x2 > 1 ?
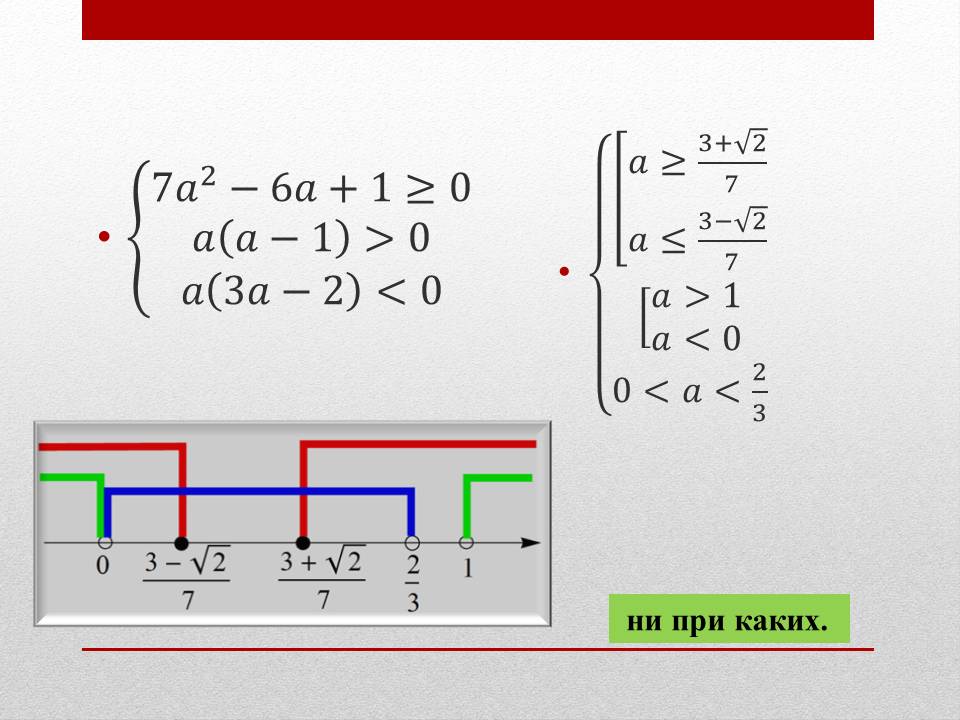
 Решение. Имеем третий случай
Решение. Имеем третий случай
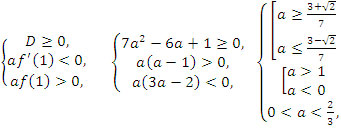
Ответ: ни при каких. (Рисунок 9)
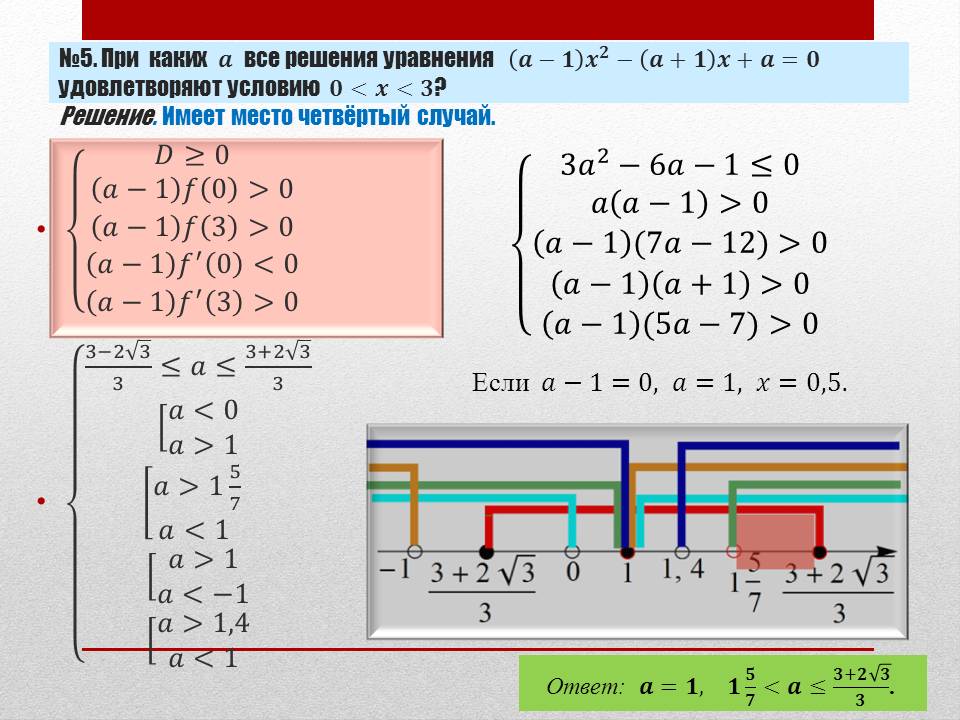
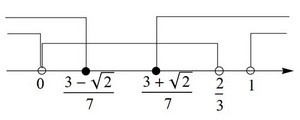
№5. При каких a все решения уравнения (a - 1)x2 - (a + 1)x + a = 0 удовлетворяют условию 0 < x < 3 ?
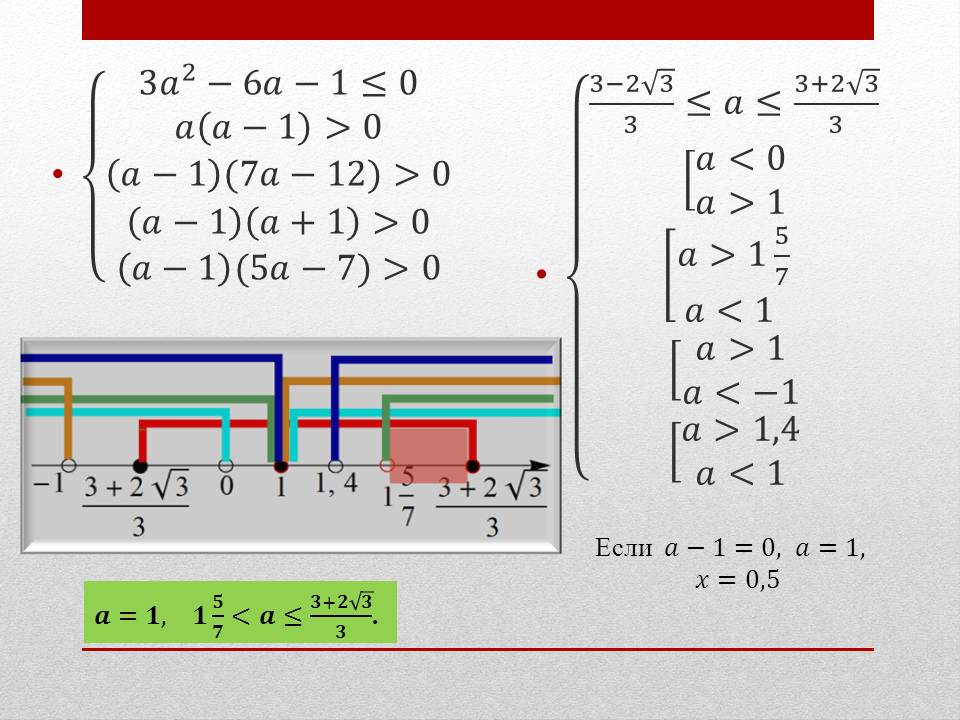
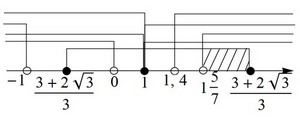 Решение. Имеет место четвёртый случай.
Решение. Имеет место четвёртый случай.
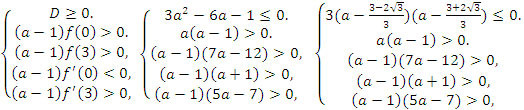
<
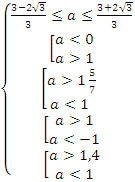
Если a - 1 = 0, a = 1, x = 0,5.
Ответ: 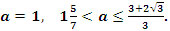 (Рисунок 10)
(Рисунок 10)
Упражнения для домашнего задания
№1. При каких c оба корня уравнения x2 + 4cx + 1 - 2c + 4c2 = 0 меньше -1?
№2. При каких a оба корня уравнения (a + 1)x2 - 3ax + 4 = 0 больше 1?
№3. При каких a один из корней уравнения x2 - (3a + 2)x + 2a - 1 = 0 больше 1, а другой меньше 1?
№4. Найти все значения a для которых один корень уравнения 2ax2 - 2x - 3a - 2 = 0 больше 1, а другой меньше 1?
№5. При каких a существует единственный корень уравнения x2 - ax + 2 = 0, удовлетворяющий условию 1 < x < 3?