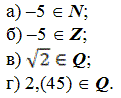Тип урока: комбинированный
Задачи урока: знакомство с понятиями множества, пустого множества, способами задания множеств; формирование навыков решения упражнений на применение нового материала и ранее изученного.
Цели урока:
- Образовательные: сформулировать понятия множества, пустого множества; рассмотреть различные способы задания и описания множеств; формировать умения применять новые и полученные ранее знания для решения упражнений.
- Развивающие: способствовать развитию мыслительной активности учащихся, логического мышления.
- Воспитательные: развивать у учащихся коммуникативные компетентности (культуру общения, умение работать в коллективе).
ХОД УРОКА
1. Мотивация
Устные вычисления
Слайд 1.
Задание на первом слайде презентации.
Задание: Найдите значение переменной, при которой не имеет смысла алгебраическая дробь:
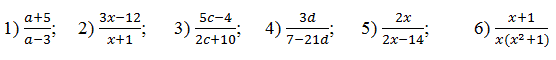
После выполнения задания перед учащимися появляется фотография Георга Кантора и его фраза о понятии множества.
2. Изучение нового материала
Учитель. Георг Кантор (19 февраля (3
марта) 1845 года – 6 января 1918 года) – немецкий
математик. Родился в Санкт-Петербурге.
Именно его принято считать основателем теории
множеств.
Уже в 70-х годах XIX века он разработал свою
программу стандартизации математики, в рамках
которой любой математический объект должен был
оказаться тем или иным «множеством». При этом
общему понятию «множества», которое
предлагалось рассматривать в качестве
центрального для математики, Кантор давал весьма
расплывчатые определения вроде: «Множество
есть многое, мыслимое нами как единое целое» [4].
Слайд 2. Запишите тему урока: «Понятие множества».
Слайд 3. Очень часто на вопрос: «Сколько?» человек отвечает: «Много!». Некоторым множествам люди дали конкретные названия.
Например, множество звёзд – созвездия, множество птиц – стая, множество дней недели, числовые множества, с которыми мы с вами встречались в 8 классе.
Далее можно учащимся предложить привести примеры самостоятельно.
Слайд 4. Знаменитый итальянский физик, механик, астроном и математик Галилео Галилей (1564-1642) писал: «Великая книга Природы написана языком математики». За многовековую историю развития человечества не только изменялись знания людей о законах природы, но и самым существенным образом менялся язык, на котором в разные времена были записаны эти законы, – язык математики.
Слайд 5. В настоящее время множество
является первичным неопределяемым понятием в
математике. Интуитивно оно представляется как
совокупность объектов произвольной природы.
Объекты, входящие в множество, называются его
элементами. Множества обозначаются заглавными
латинскими буквами, а элементы множества –
строчными латинскими буквами.
Сегодня на уроке мы с вами рассмотрим простейшие
понятия и обозначения языка теории множеств,
который вот уже более 100 лет составляет фундамент
современного математического языка.
Слайд 6. Вот, например, маленький набор
символов, с которым нам предстоит познакомиться: ![]()
Этого набора символов достаточно, чтобы
написать огромный трактат по теории множеств.
Этими знаками можно выразить огромное
количество понятий. Последний символ, ![]() – самый простой из
них – это знак пустого множества.
Программисты позаимствовали этот знак для
обозначения нуля (чтобы не путать с буквой О).
– самый простой из
них – это знак пустого множества.
Программисты позаимствовали этот знак для
обозначения нуля (чтобы не путать с буквой О).
Учащиеся в тетрадях записывают названия символов (названия появляются, если щёлкнуть левой клавишей мыши по значку).
Вывод 1. Из всего выше сказанного вы уже поняли, что множество состоит из элементов или не содержит ни одного элемента.
Слайд 7. Понятие множества таит в себе опасность появления противоречий или, как ещё говорят, парадоксов. Появление парадоксов связано с тем, что не всякие конструкции и не всякое множество можно рассматривать.
ПАРАДОКС БРАДОБРЕЯ
Это довольно известная история, и у неё есть
много версий.
В одном полку жил-был полковой парикмахер,
которого по историческим причинам называют
брадобреем. Однажды командир приказал ему брить
тех и только тех, кто не бреется сам. Брадобрей,
получив приказ, сначала обрадовался, потому что
многие солдаты умели бриться сами, побрил тех,
кто бриться сам не умел, а потом сел на пенёк и
задумался: а что ему с собой-то делать? Ведь если
он будет брить себя, то нарушит приказ командира
не брить тех, кто бреется сам. Брадобрей уже решил
было, что брить себя не будет. Но тут его осенила
мысль, что если он сам себя брить не будет, то
окажется, что он сам не бреется, и по приказу
командира он должен всё-таки себя побрить…
Что с ним стало, история умалчивает.
Причём же здесь теория множеств? А вот причём: командир пытался определить множество людей, которых брадобрею нужно брить, таким образом:
{те и только те, кто не бреется сам}.
Казалось бы, обычное множество, описывается несколькими русскими словами, чем оно хуже, например, множества
{все ученики школы}?
Но с этим множеством тут же возникает проблема:
непонятно, принадлежит ли этому множеству
брадобрей.
Столкнувшись с этими парадоксами, создатели
теории множеств осознали, что нельзя задавать
множества произвольным и словосочетаниями.
После этого они стали бороться с парадоксами
двумя способами (первый щелчок левой клавишей
мыши по слову «парадокс» на слайде –
появляется информация о первом способе; второй
щелчок – информация о втором способе; третий
щелчок – автор и название книги о парадоксах
теории множеств).
Первый способ – способ Кантора, придумавшего «наивную теорию множеств», в которой запрещаются все действия и операции, ведущие к парадоксам. Идея в следующем: разрешается работать со множествами, которые «встречаются в природе», также разрешается работать со множествами, которые получаются из них разумными теоретико-множественными операциями.
Другой способ – аксиоматический. Этот способ преодоления парадоксов развивали Цермело и Френкель (система аксиом Цермело-Френкеля), Гёдель и Бернайс (система аксиом Гёделя-Бернайса).
Согласно этой теории, множество – это нечто, удовлетворяющее аксиомам.[3]
Мы с вами немного узнали о развитии теории
множеств, окунулись в исторические сведения,
познакомились с одним из парадоксов. Кого
заинтересовала информация, я предлагаю почитать
книгу И.В. Ященко «Парадоксы теории множеств».
А мы продолжим изучение языка теории множеств.
Слайд 8.
Если множество состоит из элементов, то их
иногда можно перечислить. Такое перечисление
производят внутри фигурных скобок {, }.
Фигурные скобки у знака ![]() не ставятся, т.к. никакого перечисления
элементов пустого множества не происходит: этих
элементов просто нет.
не ставятся, т.к. никакого перечисления
элементов пустого множества не происходит: этих
элементов просто нет.
Если число элементов множества достаточно
велико или если множество бесконечно, то явное
перечисление элементов такого множества
невозможно. Способы задания, описания таких
множеств весьма разнообразны. Вот некоторые из
них:
| Множество | Словесное описание множества | Способ задания | |
| 1 | {100; 105; 110; ... 995} | Множество всех трёхзначных чисел, кратных 5 | перечисление элементов |
| 2 | {1; 8; 27; 64; ...} | Множество всех кубов натуральных чисел | |
| 3 | N | Множество натуральных чисел | используя специальные обозначения |
| 4 | Q | Множество рациональных чисел | |
| 5 | {x | 5 < x< 10} | Множество всех чисел, которые больше 5 и меньше 10 | с помощью характеристического свойства |
| 6 | (–3; 17) | Множество всех чисел, которые больше –3 и меньше 17 | числовой промежуток (интервал) |
Используемые обозначения читаются:
«...» – и так далее
«|» – таких, что
Задание множества с помощью его характеристического
свойства – один из самых распространённых
способов задания множества.
Мы с вами уже встречались с некоторыми числовыми
множествами. Давайте вспомним о них и запишем их,
используя математический язык.
Учащиеся делают записи в тетрадях и на доске.
1) Множество натуральных чисел:
N={1; 2; 3; ...}
2) Множество целых чисел:
Z={0; 1; 2; ...; n; ...; –1; –2; ...; –n; ...}
или Z={...; –n; ...; –2; –1; 0; 1; 2; ...; n; ...}
3) Множество рациональных чисел:
![]()
4) Множество действительных чисел: R – состоит из элементов, представляемых в виде конечной или бесконечной десятичной дроби.
5) ![]() – отрезок с
концами а и b.
– отрезок с
концами а и b.
6) ![]() – открытый
луч с концом в точке b.
– открытый
луч с концом в точке b.
Учитель выключает проектор (время работы которого не более 25 минут урока).
3. Закрепление изученного материала
Решение упражнений
№3.1 (а, б, в)
Множество задано словесным описанием. Задайте это множество, перечислив его элементы:
а) цифры, которые больше 5;
б) целые отрицательные числа, которые больше – 7;
в) четыре последние буквы русского алфавита.
№ 3.2 (устно)
Множество задано перечислением своих элементов. Приведите какое-нибудь его словесное описание:
а) {0, 2, 4, 6, 8};
б) {2, 3, 5, 7};
в) {3, 6, 9, ... , 27, 30};
г) {A, B, C, D, ... , X, Y, Z}.
Обратить внимание на то, что словесные описания одного и того же множества могут выглядеть по-разному. Ведь в естественном, разговорном языке одну и ту же мысль, идею и т.п. можно выразить по-разному.
№3.3 (в, г)
Запишите заданное множество в виде числового
промежутка: ![]()
Прочтём данную запись шаг за шагом.
Следует найти множество всех x таких, что x2
– 1 < 0.
Решив последнее неравенство, получим ответ.
Ответ: (– 1; 1)
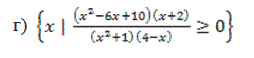
Прочтём данную запись шаг за шагом.
Следует найти множество всех x таких, что
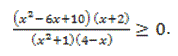
Решив последнее неравенство методом интервалов, получим ответ.
Ответ: [–2; 4)
Такие словесные обороты, как «элемент х
принадлежит множеству А» или «элемент х
является элементом множества А», достаточно
длинны и не всегда удобны в записи решений
конкретных задач. В математике эти выражения
записывают более коротко: ![]()
Запись: ![]() –
означает «элемент х не принадлежит
множеству А».
–
означает «элемент х не принадлежит
множеству А».
Решение упражнений
№3. 4 (устно)
Верно ли, что:
№3.5(а, б)
Докажите, что заданное множество состоит из одного числа (элемента), и найдите это число:
а) ![]() (устно)
(устно)
Учитель. Как вы понимаете, для доказательства достаточно решить неравенство. А данное неравенство имеет единственный корень (какой?) x=0, значит данное множество состоит из одного числа.
б) ![]() (письменно)
(письменно)
Один ученик решает неравенство у доски, остальные записывают решение в тетрадях.
№ 3.6 (а) (устно)
![]()
Учитель спрашивает у учащихся о вариантах
решения данного номера. Учащиеся высказываются:
1) решить неравенство и проверить, входит ли
число в множество решений неравенства;
2) подставить число в неравенство и сделать
вывод.
Учащиеся выбирают рациональный способ решения и устно отвечают на вопрос.
№ 3.7
а) Решите уравнение ![]()
Решение:
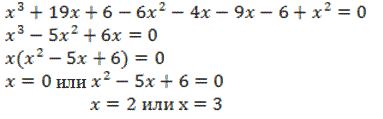
б) Запишите множество М корней этого уравнения, перечислив его элементы в порядкевозрастания.
Ответ: M={0; 2; 3}
в) Запишите все возможные способы перечисления элементов множества М.
Ответ:
0; 2; 3
0; 3; 2
2; 0; 3
2; 3; 0
3; 0; 2
3; 2; 0
г) Сколько всего имеется способов перечисления элементов множества М?
Ответ: 6.
3. Домашнее задание
§3, п.1, №3.3(а, б), 3.6(в, г), 3.17.
4. Итог урока и рефлексия
Продолжите предложение
1. Множество – это... («...многое, мыслимое нами
как единое целое»)
2. Число 5 принадлежит множеству... (Замечание:
ответ на этот вопрос не однозначный)
3. Число 3,7 множеству натуральных чисел... (не
принадлежит)
4. Сегодня на уроке я понял ... (высказываются
учащиеся по одному)
Далее учитель благодарит учащихся за работу
и оценивает результаты работы на уроке.
Учащимся можно предложить записать множество
оценок.
Источники информации
1. Алгебра. 9 класс. В 2 ч. Ч.1. Учебник для учащихся
общеобразовательных учреждений /
А.Г. Мордкович, П.В. Семёнов. –10-е изд.,
перераб. – М.: Мнемозина, 2008. – 224 с.: ил.
2. Алгебра. 9 класс. В 2 ч. Ч.2. Задачник для учащихся
общеобразовательных учреждений /
[А.Г. Мордкович, Т.Н. Мишустина и др.]; под ред.
А.Г. Мордковича. –10-е изд., перераб. – М.:
Мнемозина, 2008. – 223 с.: ил.
3. И.В. Ященко. Парадоксы теории множеств. М.:
МЦНМО, 2002.
4. Википедия
http://ru.wikipedia.org/wiki/%CA%E0%ED%F2%EE%F0,_%C3%E5%EE%F0%E3_%D4%E5%F0%E4%E8%ED%E0%ED%E4_%CB%FE%E4%E2%E8%E3_%D4%E8%EB%E8%EF%EF