Цели урока:
Образовательные:
- систематизировать пройденный материал по производным и функциям;
- научить учащихся исследовать функцию с помощью производной и строить её график;
- развивать вычислительные навыки.
Развивающие:
- умение применять полученные знания при изучении нового материала;
- развитие элементов творческой деятельности;
- развитие целеустремлённости в достижении поставленной цели.
Воспитательные:
- воспитывать самостоятельность и ответственное отношение к своему делу;
- воспитывать умение выстраивать отношения в диалоге с товарищами и учителем, чувства взаимопомощи;
- воспитание интереса к математике.
Оборудование:
- Справочный материал для библиотеки;
- Карточки для индивидуальной работы;
- Карточки для групп при составлении плана;
- Бейджики с указанием специалистов на данный урок(научный сотрудник, старший научный сотрудник, профессор, академик, журналист)
- Компьютер, интерактивная доска
Тип урока: Открытие новых знаний(изучение нового).
Форма работы: групповая, одноуровневая.
Форма занятия: Урок-игра “Научно-исследовательская лаборатория” (ролевая) с применением элементов проектно-исследовательской технологии.
Средства обучения: наглядность, ИКТ, сигнальные карточки трех цветов(синий, зеленый, красный)
Форма контроля: листы доверия, листы самооценки.
Поощрение учащихся: Вручение медалей - “Нобелевская премия” за открытие и сладкие призы.
План урока.
1.Организационный момент.
2.Актуализация опорных знаний.
а) письменная работа индивидуальная б) устная работа
3.Постановка проблемы.
4.Постановка цели урока исходя из проблемы.
5.Мотивация к достижению цели.(примеры из жизни)
6.Опорные знания для достижения цели.
7.Выявление темы урока учащимися.
8.Запись в тетрадях темы и цели урока.
9. Работа с карточками, составление плана исследования функции. Работа с учебником. Работа с библиотекой (справочным материалом).
10.Решение проблемы по плану исследования.
11.Достижение цели.
12.Вручение “нобелевской премии” учащимся, достигнувших цели.
13.Рефлексия.
14.Задание на дом.
15.Самооценка
16.Итог урока.
Ход урока
Девиз к уроку: “Решай ,ищи, твори и мысли”
1. Организационный момент.
Перед уроком оформляется библиотека, где собран необходимый материал для изучения темы. Класс разбивается на 4 лаборатории, где назначаются старший научный сотрудник и сотрудники; профессора и академик. Выбирается журналист (может и учитель быть), который в ходе работы групп интересуется решениями и проявляет любознательность.
Перед учащимися ставится задача, которую они должны решить в ходе урока, определить цель урока, сформулировать тему , достичь цели, подвести итог своей деятельности и сделать соответствующие выводы.
2. Актуализация опорных знаний.
а) письменная работа индивидуальная дифференцированная (слайд 2)
Научным сотрудникам задания:
Найти область определения.
- у = 4х2 + 2х - 5
Определить четность или нечётность.
- у= 2х3 – 4х
Найти точки пересечения графика функции с осями координат.
- у= 3х3 - 6х
Профессорам и академикам
Найти критические точки.
- у = х4 - 8х2
Найти промежутки возрастания и убывания.
- у = 12х2 + 14х
Найти точки экстремума и экстремум функции
- у = 3х3 - 6х
б) устная работа . Назвать графики известных функций. (слайд 3)
- у = -2х+5
- у = х2 + 4х - 3
- у = х2+1
- у = х2
- у = 0,5х
- у = 8
- у =
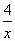
- у = х2- 2
- х = 3
- у = 3х - х3
- у = х4 -2х2 -3
3. Постановка проблемы. (слайд3)
Не умею и не знаю графики многих функций.
Выдвигаем цель: Научиться строить график незнакомой функции (слайд 4)
4. Мотивация к достижению цели.(примеры из жизни) (слайд 5,6,7,8)
Для чего нужно научиться строить график? Где пригодятся эти знания?
Функции в жизни.
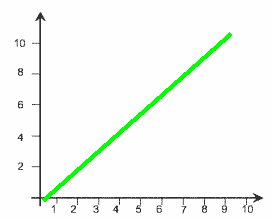
(слайд 5) Рассмотрим деление праздничного торта между гостями. Отчего зависит количество порций? – от числа гостей. А от чего зависит вес порции? – тоже от числа гостей.
Итак, чем больше гостей, тем на большее количество порций мы должны разделить торт.
Здесь наглядно можно представить прямую пропорциональную зависимость.
![]()
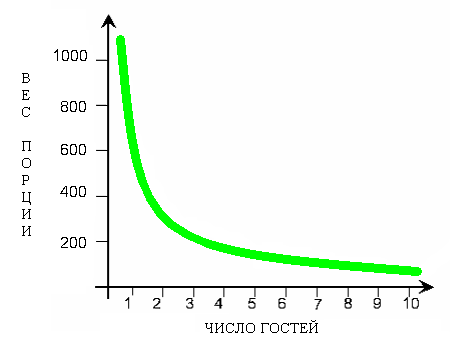
(слайд 6) - Во втором случае, чем больше гостей, тем меньше вес порции.
Здесь наглядно можно представить обратную пропорциональную зависимость.
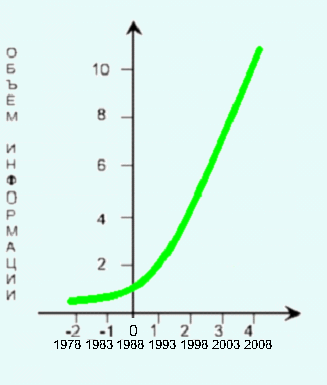
(Слайд 7)Мы живём в век информационных технологий. Ежедневно мы получаем массу информации из различных источников: телевидения, радио, газет, журналов, и, конечно, Интернета. Если построить график зависимости объёма информации от времени, то получим некоторую кривую, которая является графиком показательной функции.
(Слайд 8) В жизни часто приходится встречаться с такими фактами, когда скорость изменения какой-нибудь величины пропорциональна самой величине. Так по закону показательной функции можно рассмотреть размножение ланцетника. А так же размножение всего живого на земле, если бы для этого имелись бы благоприятные условия. Доказательство тому – распространение в Австралии кроликов, которых там раньше не было. Достаточно было выпустить пару особей, как через некоторое время их потомство стало национальным бедствием.
6. Опорные знания для достижения цели.
Вопрос учителя: Какие свойства необходимы знать для построения графика функции? (ответы учащихся, перечисляют)
Учитель: Найти ответы для нахождения критических точек, промежутков возрастания, убывания поможет... (учащиеся должны ответить что - производная)
7. Выявление темы урока учащимися. (слайд 9)
Учащиеся объединяют цель (в начале) урока и понятие производной, и формулируют тему урока.
Тема: “Применение производной к исследованию функции и построение её графика”.
8. Запись в тетрадях темы и цели урока.(слайд 9)
9. Составление плана исследования функции.
Из набора слов по карточкам составляем план в алгоритмическом порядке. Выслушиваем учащихся, корректируем. Записываем в тетрадь.
(слайд 10) План исследования.
- Найти область определения.
- Область значений (если возможно найти)
- Исследовать на чётность и нечётность, периодичность (для тригонометрических) функцию.
- Найти точки пересечения графика с осями координат (с осью Ох и осью Оу)
- Найти критические точки.
- Найти промежутки монотонности (возрастания и убывания).
- Найти точки экстремума и экстремум функции(хmax, xmin, ymax, ymin)
- Построить график.
- Если необходимо вычислить дополнительные точки.
10. Решение проблемы по плану исследования. (слайд 11)
Исследовать и построить график.
у= 3х - х3 (для научных сотрудников)
у = х4 -2х2 -3 (для профессоров)
11. Достижение цели. Работают в группах и обсуждают до первого победителя, кто построит правильно график. Проверка. (Слайд12)
Журналисты (в лице учащихся со слабыми знаниями) ходят по группам, интересуются, задают вопросы, делают записи в своих тетрадях. Получают знания с интересом.
Во время работы учащиеся обращаются к справочному материалу (библиотека), где найдут и теоретический материал по пройденным темам и образцы.
Учитель выступает в роли старшего товарища, наблюдает за ходом работы учащихся.
12. Вручение медали “Нобелевская премия” учащимся ,достигнувших цели,
и сладкий приз (слайд 13)
13. Рефлексия. Используем сигнальные карточки при ответе на вопросы.(слайд 13) .
- Чему научился на уроке.
- Смог ли понять новый материал.
- Самооценка своей деятельности.
1) Усвоил хорошо.
2) Усвоил, но есть проблемы.
3) Усвоил плохо.
14. Задание на дом. Индивидуально-дифференцированая работа. (слайд 13)
Стр. 147 – 148 всем.
№296 (в) – научным сотрудникам
№297(а) – академикам и профессорам
15. Самооценка
Заполняют листы самооценки и сдают учителю.
16. Окончание урока. Итог.