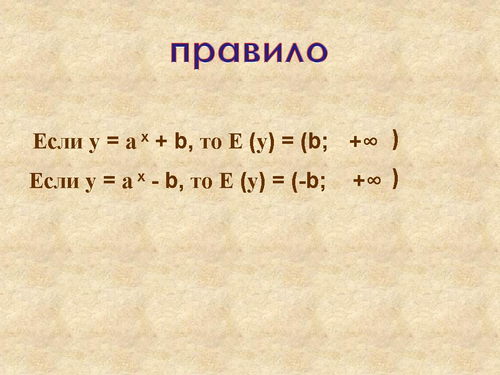Тип урока: урок изучения нового материала.
Цель урока:обеспечить усвоение учащимися знаний о показательной функции, её свойствах, создать условия для развития умений получать знания посредством проведения исследовательской деятельности и анализа ситуации.
Развивающие задачи:
- развитие памяти учащихся;
- развитие умений сравнивать, обобщать, правильно формулировать задачи и излагать мысли;
- развитие логического мышления, внимания и умения работать в проблемной ситуации.
Воспитательные задачи:
- воспитание умения работать в коллективе, взаимопомощи, культуры общения.
- развитие познавательного интереса учащихся;
- развитие любознательности учащихся;
- развитие умений преодолевать трудности при решении математических задач; воспитание таких качеств характера, как настойчивость в достижении цели;
Средства обучения:компьютер, классная доска, слайдовая презентация, интерактивная доска, учебник "Алгебра и начала анализа10-11" под редакцией А.Г.Мордковича, чертёжные инструменты, карточки.
План урока
- Орг. момент 1 мин
- Повторение пройденного материала в форме игры 3-4мин
- Новая тема 13-15мин
- Закрепление изученного материала. 21-23мин
- Подведение итогов и домашнее задание 2 мин
Ход урока
1. Орг. момент.
2. Игра "Самый умный на уроке"
Эта игра проводится с целью актуализации знаний учащихся на уроке изучения нового материала по теме "Показательная функция и ее график".
Учащемуся предлагается в течение 60 секунд отвечать на вопросы. (листочки розданы заранее)
Звание "самого умного на уроке" присваивается тому, кто ответил на большее количество вопросов. (итог в конце урока - можно приготовить мини-призы)
Вопросы:
- Независимая переменная (х)
- Наглядный способ задания функции (графический)
- График четной функции симметричен относительно чего (Оу)
- График квадратичной функции называется (парабола)
- Что обозначают буквой D (область определения)
- Способ задания функции с помощью формулы (аналитический)
- График какой функции - прямая (линейной)
- О какой функции речь? Чем больше х, тем больше у. (возрастающая)
- Свойство функции f(-x) = f(x ) (четность)
- Множество значений, принимаемых независимой переменной (область определения)
- Что обозначают буквой Е ? (область значений)
- График нечетной функции симметричен относительно чего (начала координат)
- О чем речь? Чем меньше х, тем больше у. (убывание)
- Множество целых чисел - какая буква? (Z)
- Точки пересечения графики функции с осью Ох (нули функции)
- Множество действительных чисел - какая буква? (R)
- Свойство функции f(-x) = - f(x) (нечетность)
Проверка ответов слайд№3
3. Изучение новой темы.
а) определение
Вам предстоит сегодня много рассуждать, делать выводы, спорить.
В жизни мы часто сталкиваемся с зависимостями между величин. Оценка по контрольной работе зависит от количества и правильности выполненных заданий, стоимость покупки от количества купленного товара и цен. Одни зависимости носят случайный характер, другие постоянны.
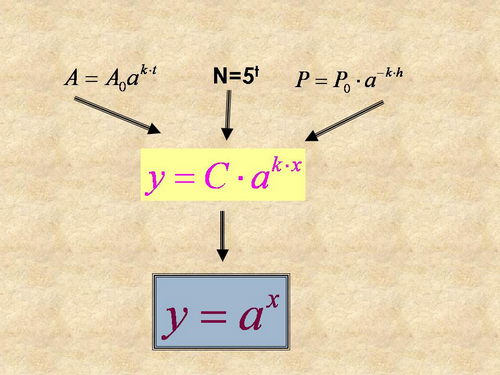
Давайте рассмотрим следующие законы. Слайд 4-6
Рост древесины происходит по закону A=A0*akt
A - изменение количества древесины во времени;
A0 - начальное количество древесины;
t - время, к, а - некоторые постоянные.
Давление воздуха убывает с высотой по закону: P=P0*a-kh
P - давление на высоте h,
P0 - давление на уровне моря,
а - некоторая постоянная.
Изменение количества бактерий N=5t
N-число колоний бактерий в момент времени t
t- время размножения
- Что общее объединяет эти процессы? Слайд №7 - схожесть вида формулы, задающей закон у=с·акх
Тема нашего урока показательная функция. Слайд №8 (запись в тетрадях)
- Положим в этих формулах с=1,к=1, какую функцию получим? - у=ах
- постройте график Слайд№9
- что это за функция?
б) практическая работа. Слайд№10
- построить графики функций на отрезк е[-2;3] с шагом 1.
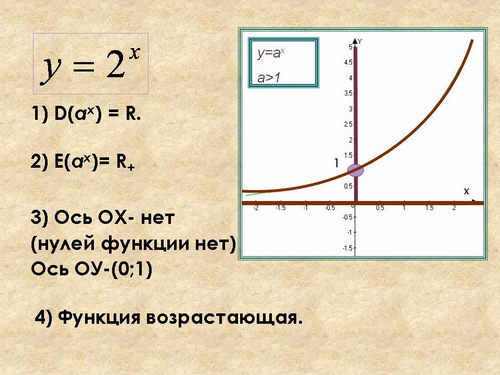
- 1 вариант у=2х,
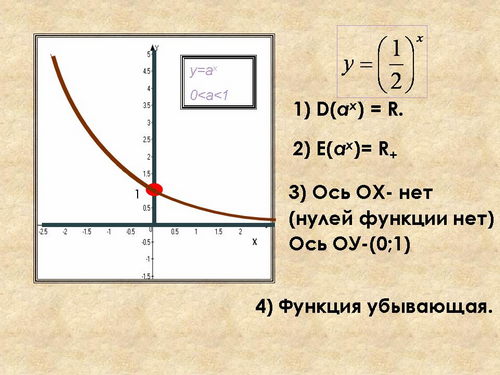
- 2 вариант у=(1/2)х
Проверим правильность ваших построений Слайд №11
Давайте сравним графики функций у=2х , у=(3/2)х , у=(5/2)х
- Какие выводы мы можем сделать? - Чем больше основание ,тем более пологий график.
А теперь сравним графики функций у=(1/2)х , у=(4/6)х, у=(1/3)х и сделаем соответствующие выводы. - Чем больше основание, тем более пологий график.
Такие функции называются показательными.
И сегодня на уроке, мы должны дать определение показательной функции, рассмотреть некоторые свойства и научится применять эти свойства при выполнении заданий, определенного вида.
Итак, попробуйте сформулировать определение показательной функции.
(учащиеся отвечают, учитель, если нужно корректирует определение).
(На слайде №12 появляется определение, учащиеся записывают его в тетрадь)
По предложенной схеме исследовать функцию. Слайд №13
Каждый вариант исследует свою функцию
1. Область определения функции.
2. Область значений функции.
3. Точки пересечения с осями координат.
4. Промежутки возрастания и убывания.
в) проверка результатов практической работы.
Слайды №14,15
На экране появляются графики функций, учащиеся называют свойства, которые демонстрируются. Ученики делают записи в тетрадях.
4. Закрепление изученного.
Я предлагаю вам выполнить некоторые задания по теме нашего урока.
а) Устно.(учащиеся выбирают верный ответ, обосновывая выбор )
1."Выбери показательную функцию".
а) Функции заранее записаны на доске
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
б). Из предложенного списка функций, выбрать ту функцию, которая является показательной: (На слайде16 )
![]()
![]()
![]()
![]()
Укажите множество значений функции:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Последняя функция - решение в тетрадь Слайд№17
3. Дана функция: у =аx + b. Вывести правило, по которому можно, не выполняя построение графика данной функции, найти область значения функции. Слайд №18-19 (правило записать в тетрадь)
Вывод:
Если у = а х+ b, то Е (у) = (b; +?)
Если у = ах -b, то Е (у) = (-b; +?)
4. Укажите возрастающую функцию. Слайд №20
![]()
![]()
![]()
![]()
5. Укажите убывающую функцию.
![]()
![]()
![]()
![]()
б) Письменно.
Используя свойства убывания или возрастания показательной функции, сравнить с единицей следующие числа: № 1322
Слайд №21
г) Самостоятельная работа (если необходимо с помощью учителя).
Приложение 1. Дидактический материал к уроку по теме "Показательная функция"
5. Домашнее задание. (на слайде №22)
6. Подведение итогов. Выставление оценок. (на слайде №23)
Фрагменты этого урока можно также использовать при повторении пройденного материала, при подготовке к экзамену.
Цветными геометрическими фигурами на слайдах показаны гиперссылки. (слайд №11,16)
В ходе подготовки данной работы использовались материалы из опыта работы: Морина С.А. - учитель математики МОУ СОШ №5 г.Железноводска.