Цели урока:
- рассмотреть теорему Пифагора и показать её применение в ходе решения стандартных задач;
- воспитание эстетических чувств учащихся: проявление эстетического вкуса и суждения;
- развитие творческого мышления, интереса к математики.
Оборудование:
- интерактивная доска, проектор;
- слайды “Теорема Пифагора”.
Ход урока
1. Сообщение темы и целей урока
(Слайд 1) Сегодня на уроке мы увидим много необычного и красивого, и поймем что математика представляет собой науку не просто о сухих числах, а науку которая очень интересная и вдохновляющая. Вперёд к знаниям!
2. Сообщение учащегося из истории математики о Пифагоре
В это время на доске демонстрируется портрет ученого (Слайд 2, 3)
Текст сообщения (источник: Википедия)[2]:
Родителями Пифагора были Мнесарх и Партенида с Самоса. Мнесарх был камнерезом. Партенида, позднее переименованная мужем в Пифаиду, происходила из знатного рода Анкея, основателя греческой колонии на Самосе.
Рождение ребёнка будто бы предсказала Пифия в Дельфах, потому Пифагор и получил своё имя, которое значит “тот, о ком объявила Пифия”. В частности, Пифия сообщила Мнесарху, что Пифагор принесет столько пользы и добра людям, сколько не приносил и не принесет в будущем никто другой. Пифагор родился в Сидоне Финикийском (по Ямвлиху) примерно в 570 до н. э.
По словам античных авторов, Пифагор встретился чуть ли не со всеми известными мудрецами той эпохи, греками, персами, халдеями, египтянами, впитал в себя всё накопленное человечеством знание.
В юном возрасте Пифагор отправился в Египет, чтобы набраться мудрости и тайных знаний у египетских жрецов. Диоген и Порфирий пишут, что самосский тиран Поликрат снабдил Пифагора рекомендательным письмом к фараону Амасису, благодаря чему он был допущен к обучению и посвящён в таинства, запретные для прочих чужеземцев.
Пифагор в 18-летнем возрасте покинул родной остров и, объехав мудрецов в разных краях света, добрался до Египта, где пробыл 22 года, пока его не увёл в Вавилон в числе пленников персидский царь Камбиз, завоевавший Египет в 525 до н. э. В Вавилоне Пифагор пробыл ещё 12 лет, общаясь с магами, пока наконец не смог вернуться на Самос в 56-летнем возрасте, где соотечественники признали его мудрым человеком.
Пифагор поселился в греческой колонии Кротоне в Южной Италии, где нашёл много последователей. В конце VI в. до н. э. Пифагору пришлось удалиться в другую греческую колонию Метапонт, где он и умер. Почти 450 лет спустя во времена Цицерона (I в. до н. э.) в Метапонте как одну из достопримечательностей показывали склеп Пифагора.
У Пифагора была жена по имени Феано, сын Телавг и дочь Мня
Дата смерти 490 до н. э. (или 480 до н. э., что маловероятно).
3. Устная работа
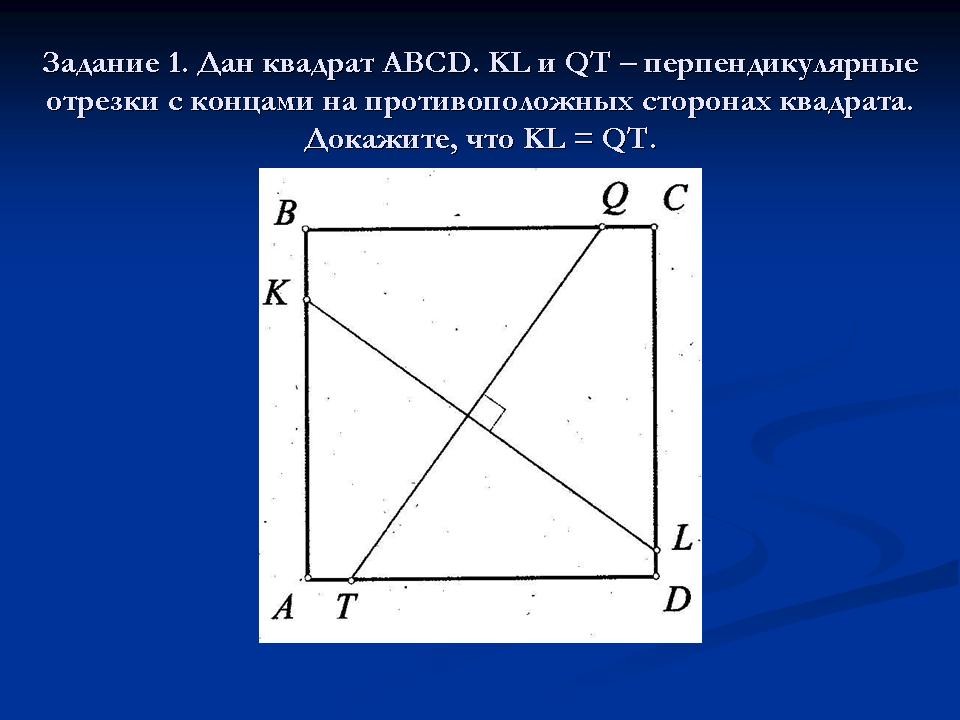
Задача. (Слайд 4) Дан квадрат ABCD <Рисунок 1>. KL и QT – перпендикулярные отрезки с концами на противоположных сторонах квадрата. Докажите, что KL = QT.
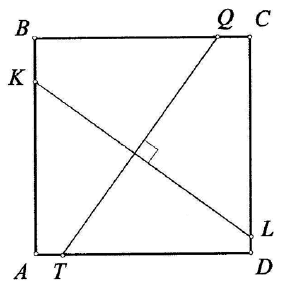
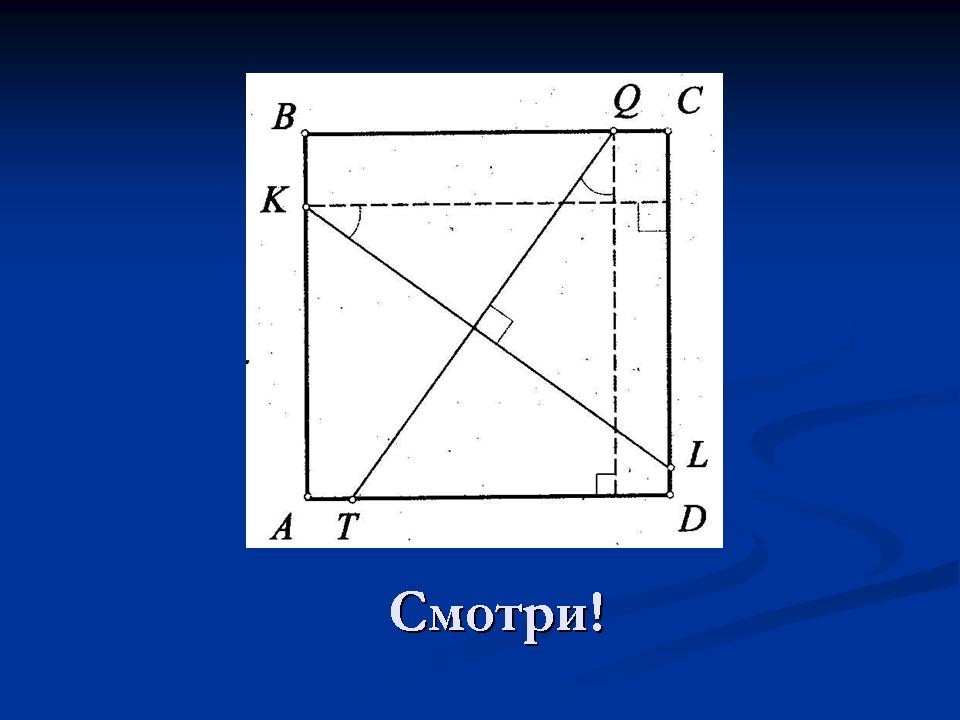
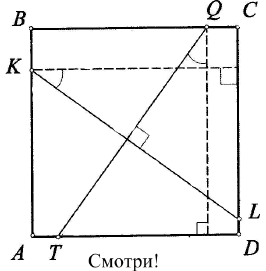
Решение задачи (Слайд 5) Посмотрите внимательно на <Рисунок 2> и скажите почему отрезки KL и QT равны.
4. Основная часть
О теореме Пифагора (Слайд 6)[3]
Уделом истины не может быть забвенье,
Как только мир ее увидит взор,
И теорема та, что дал нам Пифагор,
Верна теперь, как в день ее рожденья.
За светлый луч с небес вознес благодаренье
Мудрец богам не так, как было до тех пор.
Ведь целых сто быков послал он под топор,
Чтоб их сожгли как жертвоприношенье.
Быки с тех пор, как только весть услышат,
Что новой истины уже следы видны,
Отчаянно мычат и ужаса полны:
Им Пифагор навек внушил тревогу.
Не в силах преградить той истине дорогу,
Они, закрыв глаза, дрожат и еле дышат.
Суть истины вся в том, что нам она-навечно,
Когда хоть раз в прозрений ее увидим свет,
И теорема Пифагора через столько лет
Для нас, как для него, бесспорна, безупречна.
На радостях богам был Пифагором дан обет:
За то, что мудрости коснулся бесконечной,
Он сто быков заклал, благодаря предвечных;
Моленья и хвалы вознес он жертве вслед.
С тех пор быки, когда, учуют, тужась,
Что к новой истине людей опять подводит след,
Ревут остервенело, так что слушать мочи нет,
Такой в них Пифагор вселил навеки ужас,
Быкам, бессильным новой правде противостоять,
Что остается? – Лишь, глаза закрыв, реветь, дрожать.
А. Шамиссо
Теорема Пифагора и является основной теоремой геометрии. (Слайд 7)
А звучит она так: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
![]()
<Рисунок 3> Дано: треугольник АВС – прямоугольный, АВ = с, АС = а, ВС = b.
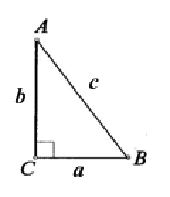
Доказать: c2 = a2 + b2.
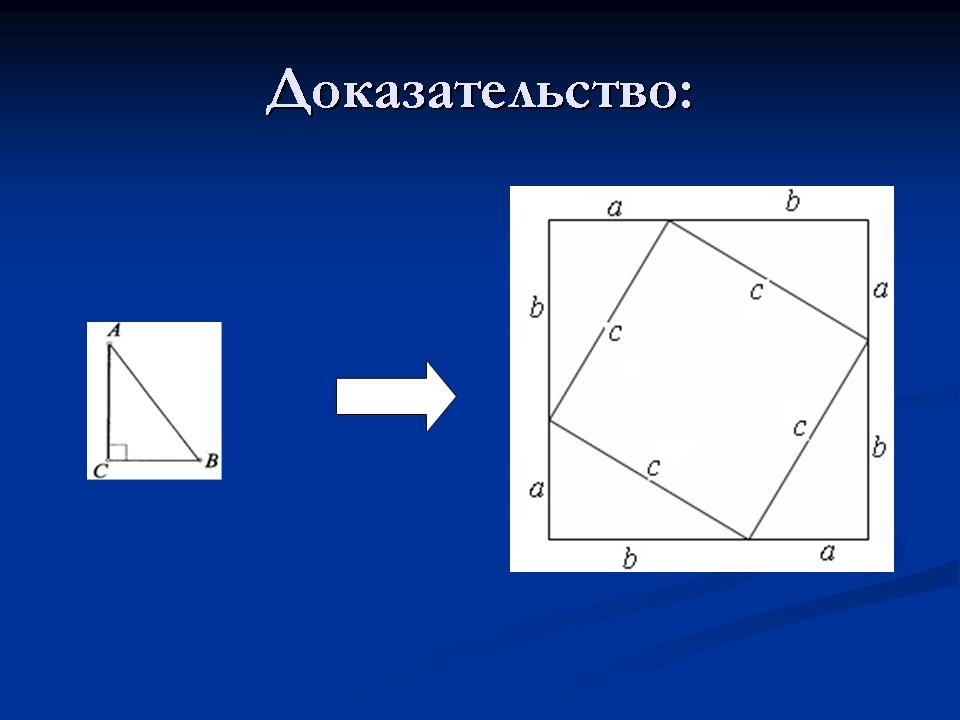
Доказательство:
(Слайд 8) 1. Достроим треугольник АВС до квадрата, сторона которого равна сумме катетов a + b. <Рисунок 4>
2. S = (a + b)2
3. S = 4• S? + c2, S? = ![]()
4. (a + b)2 = 4• ![]() + c2
+ c2 ![]() c2 = a2 + b2.
c2 = a2 + b2.
ч.т.д.
Мы изучили и доказали, как сказал Иоанн Кеплер, живший пять веков назад, “Одно из двух сокровищ геометрии. Это теорема Пифагора”.
Сейчас, решим задачу для закрепления.
(Слайд 9) №483 (а, в) Найти гипотенузу прямоугольного треугольника по данным катетам a, b: <Рисунок 3>

а) a= 6, b = 8; в) a = ![]() b =
b = ![]()
Ответ: а) с = 10, в) с = ![]() .
.
5. Исторические справки
1. В некоторых списках “Начал” Евклида теорема Пифагора называлась теоремой нимфы, по-видимому, из-за сходства чертежа с бабочкой <Рисунок 5> (Слайд 10), поскольку словом “нимфа” греки называли бабочек. Нимфами греки называли еще и невест, а также некоторых богинь. При переводе с греческого арабский переводчик, вероятно, не обратил внимание, на чертежи перевел слово “нимфа” как “невеста”, а не “бабочка”. Так и появилось ласковое название знаменитой теоремы – “теорема невесты”.
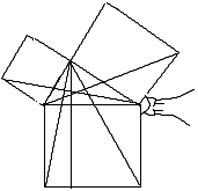
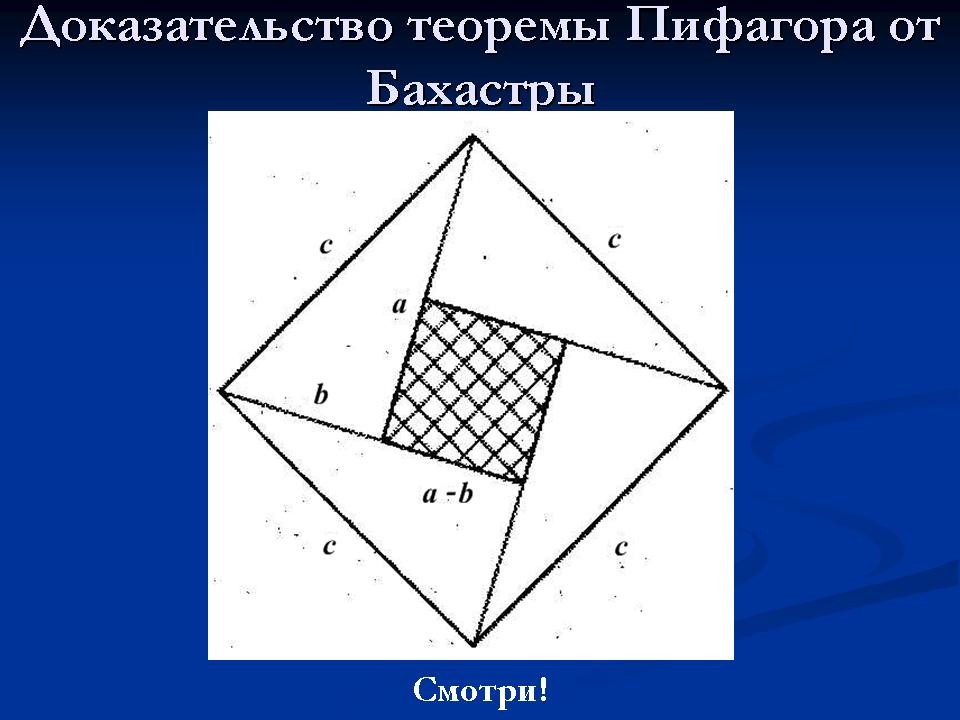
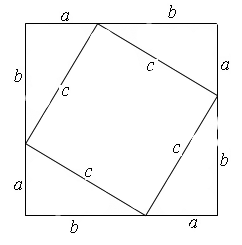
2. (Слайд 11) Рассмотрим доказательство теоремы Пифагора, которое описал индийский математик Бахастра (1114 – ок. 1178) в своём труде “Венец науки”, и это просто блестящее доказательство! <Рисунок 6>
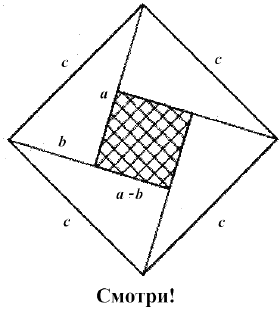
Под рисунком была лишь одна единственная подпись: “Смотри!”.
Давайте рассмотрим данное
доказательство. Площадь квадрата со стороной с
равна с2, с другой стороны он составлен
из четырёх треугольников площадь которых равна ![]() и маленького
квадрата со стороной a – b, т.е. площадью (a –
b)2 . Отсюда имеем с2 = a2 + b2.
и маленького
квадрата со стороной a – b, т.е. площадью (a –
b)2 . Отсюда имеем с2 = a2 + b2.
Такое простое и интересное доказательство, скажите разве это не прекрасно, одна теорема открытая великим учёным древности несёт в себе так много интересных и необычных доказательств, и только представьте себе сколько великих умов Земли работали над её доказательством, а их более сотни сейчас известно и многие из ни просто гениальные как только что рассмотренное.
6. Домашнее задание (Слайд 12)
Пн. 54: теорема с доказательством, сообщение из истории теоремы Пифагора (1 уч.); №483 (б, г), 484 (а, в)
7. Подведение итогов
Мы сегодня хорошо поработали. Давайте проведем рефлексию урока.
И последнее чтобы легко было запомнить Теорему Пифагора, для нас составили красивое стихотворение.
(Слайд 13) Теорема Пифагора
Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путем
К результату мы придем.
(И. Дырченко)
Литература:
1. Геометрия: 7 – 9: Учебник для общеобразоват. учреждений /Л. С. Атанасян, В. Ф. Бутусов, С. Б. Кадемцов и др. – 12-е изд. – М.: Просвещение, 2002. – 384 с.
2. http://ru.wikipedia.org/wiki/
3. http://moypifagor.narod.ru – сайт стихов про теорему Пифагора.
4. Газета “Математика”.