Круг задач, в которых применяются интегралы и их свойства, в школьном курсе математики ограничен. Более того, в классах с профильным обучением по программе не предусмотрено расширение этого круга. Классические примеры применения интегралов, перенесенные частично из вузовской программы, не в полной мере решают проблему поднятия интереса у учащихся к этой поистине важной теме начал математического анализа. Вместе с тем, на мой взгляд, этот пробел можно восполнить на элективных курсах по математике или на кружковых занятиях. Ниже приводятся задания, рассматриваемые мною с учащимися на элективных курсах в профильном классе. В них первообразная и интеграл находят неожиданные нетрадиционные применения, приносящие в изучение темы яркость и оригинальность.
Задание 1. Площадь фигуры, ограниченной
прямыми ![]() ,
, ![]() ,
, ![]() и параболой
и параболой ![]() где y
где y![]() , x
, x![]()
![]() ,
равна 15. Записать уравнение параболы.
,
равна 15. Записать уравнение параболы.
Решение. По условию задачи ![]() ,
, ![]() ,
, ![]() .
.
Отсюда получаем систему уравнений:
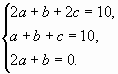
![]()
![]() ,
, ![]()
Окончательно: ![]() – точка минимума.
– точка минимума.
Задание 2. Через точку графика функции, где ![]() проведена
прямая, параллельная оси абсцисс. Для какой точки
сумма площадей криволинейных треугольников,
ограниченных данным графиком, проведенной
прямыми
проведена
прямая, параллельная оси абсцисс. Для какой точки
сумма площадей криволинейных треугольников,
ограниченных данным графиком, проведенной
прямыми ![]() и
и ![]() , будет
наименьшей?
, будет
наименьшей?
Решение. Площадь S1 равна площади прямоугольника ADEO без площади криволинейной трапеции ADO (см. рис.);
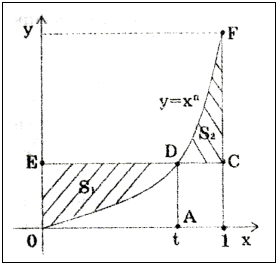
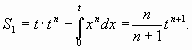
Аналогично, 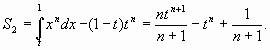 Тогда, как легко убедиться,
Тогда, как легко убедиться, ![]() обращается в 0
только при
обращается в 0
только при ![]() и
меняет в этой точке знак с минуса на плюс.
и
меняет в этой точке знак с минуса на плюс.
Следовательно, функция ![]() принимает наименьшее значение
при
принимает наименьшее значение
при ![]() .
.
Задание 3.Через точку графика строго
возрастающей и дифференцируемой функции ![]() где
где ![]() проведена
прямая, параллельная оси абсцисс. Для такой точки
сумма площадей криволинейных треугольников,
ограниченных данным графиком, проведенной
прямой и прямым
проведена
прямая, параллельная оси абсцисс. Для такой точки
сумма площадей криволинейных треугольников,
ограниченных данным графиком, проведенной
прямой и прямым ![]() и
и ![]() ,
будет наименьшей?
,
будет наименьшей?
Решение. Так же, как и в предыдущей задаче, имеем
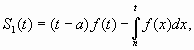
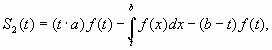

Но из формул Ньютона-Лейбница следует, что 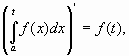
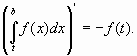
Тогда:
![]()
Так как ![]() то
то![]() при
при ![]() и меняет в этой
точке знак с минуса на плюс. Поэтому функция S(t)
принимает наименьшее значение
и меняет в этой
точке знак с минуса на плюс. Поэтому функция S(t)
принимает наименьшее значение ![]() .
.
Задание 4. По графику функции (см. рис.) ![]() вычислить
вычислить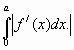
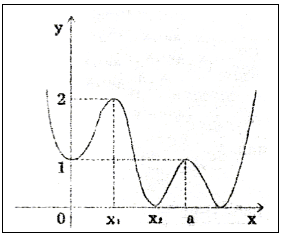
Решение. 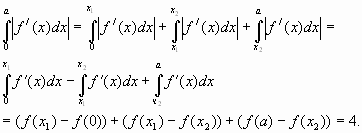
Ответ: 4
Задание 5. Найдите предел
последовательности 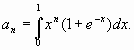
Решение. Ясно, что при ![]() будет
будет ![]() Тогда:
Тогда: 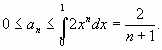 Окончательно
Окончательно ![]()
Ответ: ![]()
Задание 6. Какое из двух чисел больше: ![]() или
или ![]()
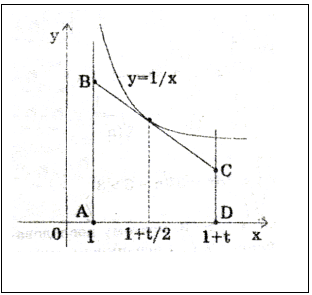
Решение. Число ![]() где
где ![]() , есть площадь криволинейной трапеции
(см.рис.). Площадь криволинейной трапеции строго
больше трапеции ABCD. Следовательно,
, есть площадь криволинейной трапеции
(см.рис.). Площадь криволинейной трапеции строго
больше трапеции ABCD. Следовательно, ![]()
Полагая ![]() получаем нужное равенство.
получаем нужное равенство.
Комментарии. Аналогично можно показать, что
![]() при
при ![]()
Тогда, при ![]() имеем
имеем 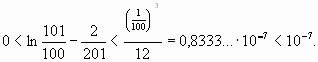 Как
видно, данные в улови задачи числа разнятся между
собой очень мало.
Как
видно, данные в улови задачи числа разнятся между
собой очень мало.
Замечание. Неравенство ![]() при
при ![]() можно доказать и с помощью
производной. Пусть
можно доказать и с помощью
производной. Пусть ![]()
Тогда: ![]() при
всех
при
всех ![]()
Следовательно, ![]() или
или ![]() для всех
для всех ![]()
Задание 7. При каком ![]() последовательность с общим
членом
последовательность с общим
членом ![]() имеет предел?
имеет предел?
Решение. Ясно, что если число ![]() , удовлетворяющее условию
задачи, существует, то оно единственно – иначе
существовал бы предел последовательности
, удовлетворяющее условию
задачи, существует, то оно единственно – иначе
существовал бы предел последовательности ![]()
Докажем, что данная последовательность имеет
предел при ![]() .
.
Поскольку при ![]()
![]() а
а ![]()
то данная последовательность убывающая.
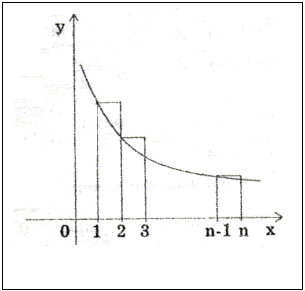
С другой стороны (см. рис.)
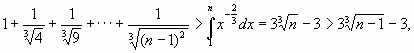 т.е.
т.е. ![]()
поэтому последовательность ![]() ограничена снизу.
ограничена снизу.
По теореме Вейрштраса она имеет предел.
Замечание. Когда внешне частичная сумма ряда интеграла напоминает интегральную сумму можно воспользоваться интегралом для вычисления суммы или оценки суммы с помощью интегральных неравенств. Но в ряде случаев, более целесообразны другие приемы. В качестве примера можно продемонстрировать решение следующей задачи.
Задание 8. Вычислить сумму, ![]() где
где ![]() для любого
для любого ![]() .
.
Решение. При ![]() имеем
имеем
![]()
Следовательно, искомая сумма равна ![]()
Комментарии. Левая часть не равна 
Тем не менее, приближенное значение этого интеграла, получаем с помощью формы трапеции, совпадает с нужным ответом, чего и следовало ожидать.
Задание 9. Доказать, что если ![]() где
где ![]() - нечетное число, то
- нечетное число, то ![]()
![]()
Решение. Так как
![]() и
и
![]() - нечетное
число, то
- нечетное
число, то ![]()
![]()
Но, как известно, ![]() причем поскольку ряд, стоящий в левой
части, является знакопеременным то
причем поскольку ряд, стоящий в левой
части, является знакопеременным то ![]() и поэтому достаточно
доказать неравенства
и поэтому достаточно
доказать неравенства ![]() и
и ![]()
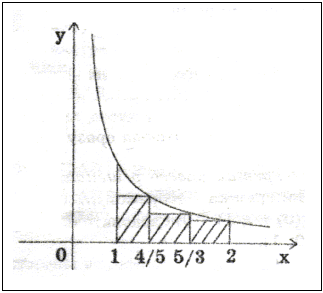
Первое из них легко доказывается по индукции, а
для доказательства второго неравенства
воспользуемся геометрической интерпретацией
определенного интеграла (см.рис.). Видно, что ![]() и поэтому
и поэтому ![]()
Задание 10. Найти все значения ![]() , при которых многочлен
, при которых многочлен ![]() имеет хотя бы
один корень интервала
имеет хотя бы
один корень интервала ![]()
Решение. Обозначив данный в условии
многочлен через ![]() , заметим, что
, заметим, что ![]() , и если
, и если ![]() не имеет корней на рассматриваемом
интервале, то как непрерывная функция он
сохраняет на этом интервале знак, т.е. для любого
не имеет корней на рассматриваемом
интервале, то как непрерывная функция он
сохраняет на этом интервале знак, т.е. для любого ![]() выполняется
неравенство
выполняется
неравенство ![]()
Но тогда интеграл 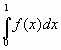 отрицателен, однако
отрицателен, однако 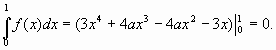
Следовательно, многочлен ![]() при любом
при любом ![]() имеет хотя бы один корень на
интервале
имеет хотя бы один корень на
интервале ![]()
Замечание. Получив, что значение ![]() положительно
при
положительно
при ![]() нельзя
считать, что эти значения являются искомыми. Ведь
полученное условие является только достаточным
(по теореме Больцана-Коши) для того, чтобы
заданный многочлен имел корень на интервале
нельзя
считать, что эти значения являются искомыми. Ведь
полученное условие является только достаточным
(по теореме Больцана-Коши) для того, чтобы
заданный многочлен имел корень на интервале ![]() , и не является
необходимым, так как функция
, и не является
необходимым, так как функция ![]() может принимать положительные
значение и между 0 и 1.
может принимать положительные
значение и между 0 и 1.
И действительно, так можно угадать, ![]() и при любых
и при любых ![]() , так что
многочлен имеет корень на интервале
, так что
многочлен имеет корень на интервале ![]() .
.
Второй способ решения. Если ![]() т.е
т.е ![]() ,
,
то ![]()
Отсюда сразу вытекает требуемое утверждение.
Третий способ решения. Воспользуемся
частным случаем теоремы Лагранжа – теоремой
Ролля: если ![]() то
то
![]() следовательно,
следовательно, ![]() обращается в 0 на интервале
обращается в 0 на интервале ![]()
Литература:
- Мамхегов А.Б. Применение интеграла при решении практических задач;
- Виленкин Н. Математика или программатика //Ж.Математика и образование 1990г;
- Казиев В.М. Математическое моделирование и вычислительный эксперимент.