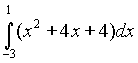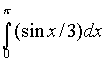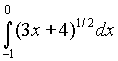Компьютер стремительно и прочно входит в нашу жизнь на правах нового орудия труда, позволяющего освободить человека от выполнения рутинных операций: счета, запоминания и поиска информации и т.д. Процесс компьютеризации общества приводит к кардинальным изменениям в структуре профессиональной деятельности человека, так как открываются дополнительные возможности для творческой работы.
Сегодня обучать нужно так, чтобы знания приобрели силу убеждения, необходимо изучать и использовать индивидуальные интересы наших учеников. Необходимо помогать учащимся, овладевать наиболее продуктивными методами учебно-познавательной деятельности. Нужно логически увязывать неизвестное с неизвестным, приучать думать и действовать самостоятельно. Творческое мышление надо развивать анализом проблем, практиковать творческие задания, чему я и следую.
Я поощряю исследовательскую работу школьников, нахожу возможность ознакомить их с техникой приближенных вычислений, алгоритма решения некоторых задач с использованием персонального компьютера.
Применяемый мною исследовательский метод позволяет свести мою деятельность к оперативному управлению процессом решения проблемных задач. В младшем звене применяю дидактические игры, которые стимулируют познавательный интерес. В качестве обучающего контроля использую программированный контроль с использованием компьютера. Создан пакет тестов для 5-го класса с использованием ПК.
Развитие творческих, познавательных способностей учащихся через ситуации успеха на уроке достигается путем использования элементов программирования и компьютеров на уроке математики.
Интегрированный урок: Приближенные методы вычисления интегралов. (2 часа)
Урок является показателем групповой творческой работы учащихся, отчетом о проделанной домашней исследовательской работе.
Цель урока: рассмотреть приближенные методы вычисления интегралов на основании геометрического смысла интеграла.
Тип урока: комбинированный.
Структура урока:
- Организация работы.
- Сообщение темы, цели, задач урока.
- Проведение теста, который носит проверочный, повторительный характер на предмет получения новых знаний.
- Систематизация основных теоретических положений. Решение задач на выяснение геометрического и физического смысла интеграла.
- Подведение итогов урока, задание на дом. Обмен мнениями по уроку.
Описание некоторых этапов урока.
Тест. Тема “Интеграл”.
Вариант 1.
1) Вычислите:
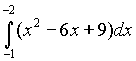
Ответ: а) 27 б) 24 в) 18 г) 21
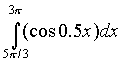
Ответ: а) -2 б) 2 в) -3 г) 3
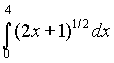
Ответ: а) 26/3 б) 28/3 в) 15/2 г) 47/6
2) Найдите интеграл: 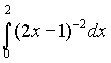
Ответ: а) 1.5 б) 2/3 в) -2/3 г) не сущ.
3) При каком значении “а” выполняется
равенство 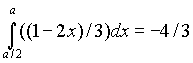 ?
?
Ответы: а) 2/3 б) 8/3 или -2 в) 2 или -1/3 г) -3
4) Вычислите площадь фигуры, ограниченной графиками функций: у=f(x), y=0, Y=-x2+x+2
Ответы: а) 13/3 б) 29/6 в) 16/3 г) 4,5
Вариант 2.
1) Вычислите:
Ответы: а) 25/3 б) 28/3 в) 26/3 г) 29/3
Ответы: -3.5 б) 1.5 в) -1.5 г) -3.5
Ответ: а) 22/9 б) -14/9 в) -22/9 г) 14/9
2) Найдите интеграл. 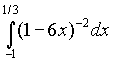
Ответ: а) 0 б) -12 в) не сущ. Г) 12
3) При каком значении “а” выполняется
равенство 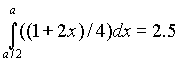 ?
?
Ответы: а) 2, -13/3 б) -4 в) 4, -5/2 г) -3,9/4
Вычислите площадь фигуры, ограниченной графиками функций: у=f(x), y=0, Y=-x2+4x-3
Ответы: а) 4/3 б) -1,5 в) 11/6 г)7/6
4) Предлагается решить задачу с использованием физического смысла определенного интеграла.
Зная скорость v = v(t) прямолинейного движения
точки, можно найти пройденный ею путь за
промежуток времени 0 ![]() t
t ![]() T.
T.
Предполагая, что траекторией точки является ось Ох и х = х(t) – есть уравнение движения, будем иметь: v(t)=dx/dt. Отсюда dx=v(t)dt.
Интегрируя это равенство в пределах от 0 до Т, получим путь, пройденный точкой за время Т:
S=x(T)-x(0)=![]() (t)dt.
(t)dt.
Точнее, эта формула дает приращение абсциссы движущейся точки за время Т.
Пройденный путь получится в том случае, когда скорость v(t)сохраняет знак, т.е. точка движется в одном и том же направлении.
Классу предлагается решить задачу.
На какую высоту за 10с поднимется ракета, запущенная вертикально вверх, если скорость меняется по закону:
V= [2+1/(t+1) 2 ]км/с?
Чему равна средняя скорость полета ракеты за этот промежуток времени?
Решение:
Путь, пройденный ракетой за 10с, равен S=![]()
![]() км/с.
км/с.
Функция f(x) = 2+1/(t+1)2 –непрерывная на [0;10] и принимает положительные значения на этом интервале. Согласно формуле Ньютона-Лейбница имеем: s=21 км.
Поэтому соответствующая средняя скорость ракеты равна: V cр=21/10=2,1км/с.
Ответ: 21км, 2,1км/с.
В качестве применения изученных знаний в новых практических ситуациях, решается задача, выясняющая геометрический смысл интеграла.
Задача:
Пользуясь геометрическим смыслом, найти
значение интеграла: I=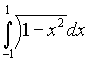
Решение:
Так как функция y (x)=(1-x2)0.5 задает
верхнюю полуокружность х2+у2=1, у ![]() 0, то
интеграл I представляет собой площадь полукруга
радиуса 1. Поэтому I =
0, то
интеграл I представляет собой площадь полукруга
радиуса 1. Поэтому I = ![]() /2; этот результат можно получить
непосредственным вычислением интеграла.
/2; этот результат можно получить
непосредственным вычислением интеграла.
Ответ: ![]() /2
/2
Часто на практике сталкиваясь с интегралами, которые не сводятся к конечной комбинации элементарных функций, следовательно, мы не можем их вычислить, пользуясь традиционными методами.
Пример: 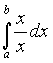
Однако, пользуясь геометрическим смыслом интеграла, можно дать ряд приближенных формул, с помощью которых этот интеграл находится с любой точностью. Рассмотрим первую из них – формулу прямоугольников.
Группа №1.
Еще свыше 200 лет тому назад греческие
математики для приближенного вычисления площади
употребляли следующий прием: разбивали
криволинейную трапецию на большое число
вертикальных полосок, ограниченных
перпендикулярами Ох, проведенных в точках х0
= а, х2,……., хn= b. Каждую полоску можно
считать за прямоугольник с основаниями ![]() хi=хi+1-
xi (i=1,2,……, n-1).
хi=хi+1-
xi (i=1,2,……, n-1).
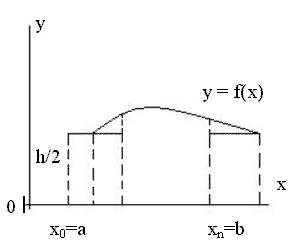
Следовательно, площадь ступенчатой фигуры, состоящей из n таких прямоугольников, будет равна их площади, где h = xi+1- xi(i=1,2,…..n-1).
Тогда площадь нашей ступенчатой фигуры будет выражаться формулой:
S = h(f(x0+h/2)+f(x0+h/2+h) +………..+ f(x0+h/2+h(n-1))).
При большом числе разбиений криволинейной трапеции на прямоугольные полоски, эти полоски в пределе обращаются в ординаты графика функции у=f(x).
Программу будем писать для конкретного
примера: 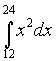
Блок-схема алгоритма №1.
- Разберем нашу блок-схему.
- Первый блок – это команда запуска программы.
- Ввод данных. Входными данными являются верхний предел интегрирования “в”, в=24, “а”-нижний предел интегрирования, а=12, n=10400 – число разбиений на прямоугольники.
- Дальше идет вычислительный процесс, где находим значение h=(b-a)/n – ширина прямоугольника, первое значение переменной х, х=а+h/2, в котором находим значение функции: s=x * x.
- Следующим блоком является блок выбора направления выполнения алгоритма в зависимости от текущей погрешности вычислений: b – x >0,001. Если выбрано решение “да”, то выполняется вычислительный процесс в цикле с предусловием, если – “нет”, то мы выходим из цикла, вычисляем конечное значение площади криволинейной трапеции и выдаем его на печать, останавливаем работу программы.
Предлагается классу написать программу на языке QBASIC.
Группа №2.
Рассмотрим формулу трапеций.
Определенный интеграл от заданной непрерывной функции у=f(x) точно вычисляется далеко не всегда. Однако, пользуясь его геометрическим смыслом, можно дать формулу трапеций для приближенного вычисления определенного интеграла.
Разобьем отрезок [a,b] на n равных частей длины h=(b-a)/n – шаг разбиения. Пусть x0, x2, …….., xn (x0=a, xn=b) – абсциссы точек деления, у0, у2, ……….уn – соответствующие ординаты кривой.
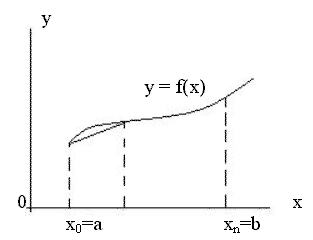
В результате построения наша криволинейная
трапеция разбилась на ряд вертикальных полосок
одной и той же ширины h, каждую из которых
приближенно примем за трапецию. Суммируя площади
этих трапеций, будем иметь 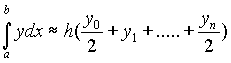
Блок-схема аналогичная предыдущей.
Предлагается классу скорректировать программу согласно новому алгоритму.
Группа №3.
Параболическая формула. Метод Симпсона.
Более точную формулу мы получим, если профиль криволинейной трапеции будем считать параболическим. Рассмотрим вертикальную полоску, ограниченную непрерывной кривой у=f(x), осью Ох, вертикальными прямыми х=-h, x=h.
Если h-мало, то кривую у=f(x) приближенно заменим параболой.
График которой проходит через точки А(-h,y-1),
B(0,y0), C(h,y1), тогда 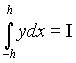 будет равен
будет равен 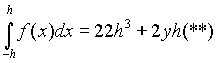
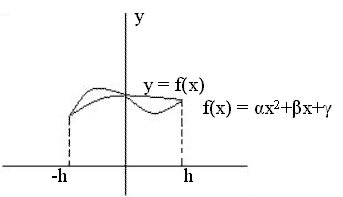
Подставим последовательно в формулу у=![]() x2+
x2+![]() x+
x+![]() x=-h, x=0, x=h,
x=-h, x=0, x=h,
получим: y-1=![]() h2-
h2-![]() h+
h+![]() , y0=
, y0= ![]() y1=
y1=![]() h2+
h2+![]() h+
h+![]() Подставим полученные выражения в (**),
получим:
Подставим полученные выражения в (**),
получим:
![]() =
=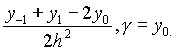 ?
?
І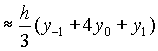 - ф.
Симпсона
- ф.
Симпсона
І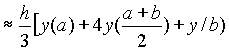 -
формула Симпсона. (****) h=
-
формула Симпсона. (****) h=![]() .
.
Используя параллельный перенос системы координат, эту формулу можно переписать в виде: (****) Томас Симпсон (20.8 1710 г. – 14.5 1761 г.) – английский математик, член Лондонского королевского общества, профессор. Был ткачом шелковых тканей, математику изучил самостоятельно. Основные труды по геометрии, в 1743 году вывел формулу приближенного интегрирования.
Для увеличения точности вычисления определенного интеграла промежуток интегрирования разбивают на n частичных промежутков, где n – достаточно большое натуральное число и к каждому из них применяем формулу Симпсона, полагая h=(b-a)/2n.
Рассмотрим блок-схему.
- Начало процесса.
- Ввод данных. Преобразование данных в форму, пригодную для обработки, частичного отрезка.
- Выбор решения, в зависимости от критерия нашего итерационного цикла.
Если разность между конечным и предпоследним значениями переменной х меньше 0,001, то выходим из цикла, выводим на печать конечный результат, иначе считаем площадь очередной малой криволинейной трапеции и прибавляем его к предыдущему значению площади и опять переходим к выбору решения.
Пример: Пользуясь формулой Симпсона, найдем – Точное значение – на основании формулы Ньютона-Лейбница. Предлагается классу написать программу на языке QBASIC.
Входными данными являются а=-3,14/2:b=3,14/2, подынтегральная функция – y=cos(x).
Вывод.
На основании геометрического смысла определенного интеграла рассмотрели приближенные формулы: прямоугольников, трапеций, парабол, которые позволяют вычислять интегралы, не сводящиеся к конечной комбинации элементарных функций.
Домашнее задание. Комментарий к решению домашнего задания.
Валеологическая минутка.