Модернизация российского образования состоит в его содержательном и структурном обновлении. Основной задачей обучения на современном этапе является формирование ключевых компетенций, необходимых для практической деятельности каждого человека.
В своей деятельности каждый современный учитель стремится к тому, чтобы наши дети умели вступать в диалог и были понятыми, свободно владели информационными технологиями, были способны к самоопределению и самообразованию.
Ключевые компетенции рассматриваются, как готовность учащихся использовать усвоенные знания, умения, способы деятельности в реальной жизни для решения практических задач. Приобретение этих компетенций базируется на опыте деятельности учащихся в конкретных ситуациях. Овладение ключевыми компетенциями позволяют человеку быть успешным и востребованным обществом. Одной из значимых составляющих Приоритетного национального проекта “Образование” является информатизация образовательного пространства школ, которая включает в себя их оснащение современной техникой, позволяющей в полной мере реализовывать информационно-коммуникационные технологии обучения.
Информационные технологии стали неотъемлемой частью общества и оказывают влияние на процессы обучения и систему образования в целом.
Применение презентаций на уроке позволяет:
- более качественно реализовать принципы наглядности и доступности при обучении,
- эффективнее использовать время на уроке.
- создавать проблемные ситуации на уроке, что активизирует познавательную деятельность учащихся.
Среди технических новинок, приходящих сегодня
в школу, особое место занимают интерактивные
доски. Интерактивная доска – уникальное
учебное оборудование, представляющее собой
сенсорный экран, подсоединенный к компьютеру,
изображение с которого передает на доску
проектор. В отличие от обычного мультимедийного
проектора интерактивная доска позволяет не
только демонстрировать слайды и видео, но и
рисовать, чертить, наносить на проецируемое
изображение пометки, вносить любые изменения, и
сохранять их в виде компьютерных файлов. А кроме
этого, сделать процесс обучения ярким, наглядным,
динамичным.
Работа с интерактивными досками предусматривает
творческое использование материалов.
Подготовленные тексты, таблицы, диаграммы,
картинки, музыка, карты, тематические CD-ROMы, а
также добавление гиперссылок к мультимедийным
файлам и Интернет-ресурсам сэкономят время на
написание текста на обычной доске или переход от
экрана к клавиатуре. Все ресурсы можно
комментировать прямо на экране и сохранять
записи для будущих уроков. Файлы предыдущих
занятий можно всегда открыть и повторить
пройденный материал. Учитель всегда имеет
возможность вернуться к предыдущему этапу урока
и повторить ключевые моменты занятия, зайдя на
нужную страницу. Все это помогает планировать
урок и благоприятствует течению занятия.
Таким образом, очевидны преимущества использования интерактивной доски на уроке:
1. Экономия времени. Заранее подготовленные чертежи, схемы, текст позволяют экономить время урока, за счет чего повышается плотность урока.
2. Наглядность и интерактивность. Благодаря этому учащиеся активно работают на уроке. Повышается концентрация внимания, улучшается понимание и запоминание материала.
3. Многократное использование. Во-первых, вся информация, появляющаяся на доске не стирается, а сохраняется. Для решения новой задачи используется “чистый лист” и в случае возникновения вопросов можно быстро вернуться к ранее решенным задачам, следовательно, нет необходимости восстанавливать условие или решение. Это наиболее существенно, так как задания и решения могут быть восстановлены не только на уроке, но и после него для тех учеников, которые пропустили урок или не вполне хорошо освоили тему. Во-вторых, наглядные материалы и обучающие ресурсы можно хранить в электронном виде и в дальнейшем многократно использовать их. Накапливается электронный банк данных для каждого учителя.
По данным анкетирования психолога школы за три последних года наблюдается позитивная динамика изменения уровня мотивации учащихся к предмету.
Урок - игра по теме “Линейная функция и её график”
Урок предназначен для учащихся 7-го класса, которые изучают алгебру по учебнику А.Г.Мордкович. В разработке применяется классическая пятибалльная система. Всем этапам занятия сопутствует компьютерная презентация, помогающая обеспечить урок качественными, быстро сменяющимися иллюстрациями, графиками и таблицами.
Цели урока:
Обучающие цели:
- обеспечить повторение учащимися изученного материала, наиболее общих и существенных понятий и алгоритмов.
- предоставить учащимся возможность использовать приобретенные знания при решении задач разного содержания и уровня сложности.
- обеспечить проверку усвоения учащимися изученного материала.
Воспитательные цели:
- создать условия для осознания необходимости самостоятельных действий при решении проблем;
- обучать объективной оценке своих возможностей и успехов;
- формировать навыки работы в заданном темпе;
- способствовать развитие навыков устной речи, умения грамотно вести диалог и аргументировать свои действия;
Интеллектуально-развивающие цели:
- создать условия для развития наблюдательности, памяти и внимания учащихся;
- способствовать развитию навыков работы с большими объемами информации: поиску, отбору, анализу, оформлению необходимого материала;
- создать условия для проявлений творческого подхода к учебным задачам, выдвижению гипотез, постановке проблем и поиску путей их решения.
План урока:
- Организация начала занятия.
- Вступление. Постановка цели и мотивация учебной деятельности учащихся. Инструктаж по организации работы на уроке.
- Проверка домашнего задания. Выводы о сфере практического применения производной.
- Повторение и анализ основных теоретических фактов, ознакомление с историческими событиями, связанными с изучаемой темой.
- Проверка знания учащимися основных теоретических фактов. Применение знаний в стандартных или частично измененных ситуациях.
- Подведение итогов.
- Самооценка. Выставление оценок учащимся.
Ход урока
I. Организационный момент.
Дежурные собирают домашние работы на проверку. Учитель приветствует учащихся, усаживает, настраивает на работу.
Урок я начну с шуточного стихотворения о линейной функции:
Функция линейная
Совсем не здоровенная
Y = k x + b и все...
И больше ничего.
Но это только кажется,
Что все легко и вяжется,
Ведь главные у функции
Есть два таких числа.
Чтоб мы не заблудились
В координатной плоскости,
Они как два гаишника
Движением рулят.
k смело нам укажет
Что за приключения
Нам с вами предстоят.
Ведь от ее характера
И от ее одежды
Зависит - то ли в горку,
Иль с горки нам бежать.
А b за нас волнуется,
b просто нам подскажет
Как правильно и верно
Дорогу перейти.
И судя по строительству
Графиков линейных,
Сказать мы можем смело,
Что числа те важны!
II. Вступление. Постановка цели и мотивация учебной деятельности учащихся. Инструктаж по организации работы на уроке.
“Да, путь познания не гладок.
Но знаем мы со школьных лет,
Загадок больше, чем разгадок
И поискам предела нет.”
Условия игры:
- Класс разбить на шесть команд.
- В каждой команде один участник, один помощник, два-три болельщика.
- За правильный ответ команда получает 5 баллов.
- При ошибки помощника команда получает 4 балла.
- При ошибки участника команда получает 3 балла.
- Болельщики отвечают на каждый вопрос.
Критерий выставления оценок
- От 80 баллов до 60 баллов - “5”
- От 59 баллов до 40 баллов - “4”
- Менее 39 баллов ставится “3”
Первый тур.

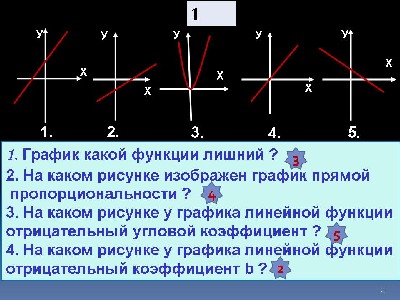
- График какой функции лишний ?
- На каком рисунке изображен график прямой пропорциональности ?
- На каком рисунке у графика линейной функции отрицательный угловой коэффициент ?
- На каком рисунке у графика линейной функции отрицательный коэффициент b ?
Ответы 3. 4. 5. 2.
Второй тур.
- Из букв расположенных на звездах составить самое длинное слово по теме урока.
А К Р И Ф Т Г О
Ответ График.
Третий тур.
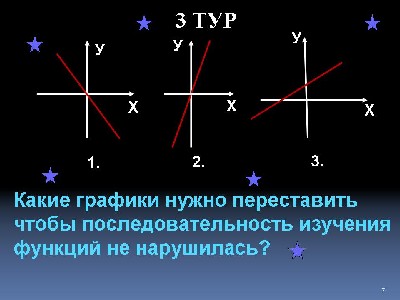
- Какие графики нужно переставить чтобы последовательность изучения функций не нарушилась?

Ответ 1 и 3.
2. На рисунке изображены графики следующих функций: у = 3х; у = - 3 х; у = х – 3.

Под каким номером изображен график функции у=-3х ?
Ответ 3.
3. Ученик допустил ошибку при построении графика одной из функций. На каком рисунке эта ошибка?

Ответ 2.
4. Найдите наибольшее значение функции у=-2х+3 на (-1;1) ?
Ответ 5.
5. Задайте формулой линейную функцию, график которой параллелен прямой у=-8х+11 и проходит через начало координат?
Ответ у = - 8 х
6. Какие точки принадлежат графику линейной функции у=-0,5х+1 1. (-1;0); 2. (-2;2,5); 3. (-2;0); 4. (0;1).
Ответ 4.
7. При каком значении х значение функции у = - 0,5х+1 равно5?
1. 8; 2. -8; 3. 9; 4. -9.
Ответ 2.
8. Назовите функции, графики которых пересекаются в одной точке?
1. у=-2х-1, у=-2х-3,5, у=-2х+5
2. у=-0,5х , у=0,5х-3, у=1,5х+5
3. у=-3х-4, у=3х-4, у=5х-4
Ответ 3.
Финал.
Составить наибольшее количество слов из букв, образующих слово.
КООРДИНАТА.
Подведём итоги. Сообщение о Рене Декарте.
Рене Декарт (1596–1650)
1) Рене Декарт родился 21 марта 1596 года в маленьком городке Ла-Гэ в Турени. Род Декартов принадлежал к незнатному чиновному дворянству. Детство Рене провел в Турени, славившейся садами, плодородием и мягкостью климата. В 1612 году Декарт закончил школу. Он провел в ней восемь с половиной лет.
В дневнике Декарта есть заметка: “10 ноября 1619 года я начал понимать основания чудесного открытия”. Не подлежит сомнению, что чудесным открытием, о котором говорит здесь Декарт, было открытие основ аналитической геометрии. Сущность аналитической геометрии состоит в приложении алгебры к геометрии и обратно – геометрии к алгебре. Всякая кривая может быть выражена уравнением между двумя переменными величинами, и обратно – всякое уравнение с двумя переменными может быть выражено кривой. Это открытие имело громадное значение не только для математики, в истории которой оно составило эпоху, но и для естественных наук, и вообще, для все расширяющегося круга знаний, имеющих дело с точными величинами – числом, мерой и весом.
Только в 1644 году Декарт издал более обширное сочинение под названием “Начала философии”. В него, наконец, вошли сочинения Декарта о мире (космосе), которые он намеревался издать еще в 1633 году. В феврале 1650 год Декарт заболевает, и на девятый день болезни 11 февраля умирает.
2) О создании прямоугольной системы координат. Полярная система координат. Вклад Декарта в развитие математики.
Более чем за 100 лет до нашей эры греческий учёный Гиппарх предложил провести на карте Земли параллели и меридианы. Таким образом, возникли хорошо всем известные Географические координаты: широта и долгота, которые обозначаются цифрами. В 14 веке французский учёный Оресле по аналогии с географическими координатами создал координатную плоскость. Он поместил на плоскость прямоугольную сетку и назвал широтой и долготой то, что сейчас мы называем абциссой и ординатой. Термины абцисса и ордината были введены в употребление Лейбницем в 17 веке. Однако основная роль в создании метода координат принадлежит французскому учёному Рене Декарту. Трудно переоценить значение декартовой системы координат для развития математики и её приложений.
Наряду с декартовой системой координат существуют и другие. Например, полярная система координат. Чтобы построить эту систему, необходимо отметить на плоскости некоторую точку О – полюс (отсюда и название – полярная система). Чтобы определить координаты точки, нужно соединить её с точкой О, определить длину отрезка и величину угла между между этим отрезком и полярной осью. Направление полярной оси можно выбрать произвольно. Так, географы за направление полярной оси выбирают направление на Север, а полярный угол называют азимутом. Артиллеристы же отсчитывают азимут от направления на Юг.
Главная заслуга Декарта заключается в том, что он создал аналитическую геометрию, в которой геометрические задачи переводятся на алгебраический язык методом координат. Кроме того, Декарт предложил неизвестные обозначать латинскими буквами x,y,z; коэффициенты – буквами a, b, c; степени – в виде x2, y3, a7 и т.д.
Декарту принадлежит теорема алгебры, формулировка которой имеет вид: “Число корней любого алгебраического уравнения равно его степени”. Эта теорема доказана была лишь в 18 веке математиком Гапсом. Однако интерес Декарта не ограничивался одной математикой, он также занимался механикой, оптикой, анатомией, биологией.
(Презентация учеников. Домашнее задание. )
| Оценочный лист | ||||
| Задания для всего класса | Основные виды работ | Максимальное кол-во баллов | Самооценка | От 80 баллов до 60 баллов - “5” От 59 баллов до 40 баллов - “4” Менее 39 баллов ставится “3” |
| Первый тур | 20 | |||
| Второй тур | 5 | |||
| Третий тур | 40 | |||
| Финал | 5 | |||
| Творческий тур. Подготовка исторической справки. Итого | 10 80 баллов |
|||