Отношение (концентрация). 6-й класс
Скачать презентацию (514.31 КБ)
Цель: создать условия для формирования умений решать задачи на растворы на основе знаний процентов, отношений и умений работы с дробями.
Задачи:
Образовательные
- повторить понятия проценты, отношения;
- закрепить знания, умения и навыки решения задач на нахождение числа по его дроби и нахождение дроби от числа, работы с дробями;
- показать практическую значимость математических знаний для решения задач на концентрацию.
Воспитательные
- показать практическую значимость математических знаний для решения задач на концентрацию из повседневной жизни;
- воспитание у учащихся интереса к предмету.
Развивающие
- развивать наблюдательность, логическое мышление учащихся;
- развивать жизненную смекалку и интуицию.
Необходимое оборудование и материалы: доска, мел, карточка с задачами, презентация.
План урока:
- Мотивационный момент (1 минута).
- Подготовка учащихся к сознательному усвоению нового материала (5 минут).
- Изучение нового материала (12 минут).
- Решение задач на отработку формул (3 мин).
- Физминутка (1 минута).
- Первичное закрепление нового материала (15минут).
- Рефлексия (1 минута).
- Подведение итогов. Домашнее задание (2 минуты).
Ход урока
I. Мотивационный момент.
Ребята, мы с вами решали задачи, содержащие проценты. Мы также знаем, что отношения существуют и между людьми, и между числами, и между величинами. Они часто встречаются в задачах. А могут быть отношения и проценты в задачах на смеси и растворы? Ответ на этот вопрос найдем на уроке.
II. Подготовка к сознательному усвоению нового материала.
(Слайд 2)
- Выразить десятичной дробью, а потом обыкновенной: 25%, 10%, 50%, 75%, 125%.
- Указать в виде процентов: 0,7; 0,04; 1,3.
- Найти 15% от числа 60.
- Найти число, 15% которого равны 30.
- Из 25 семян взошло 24 семени. Найдите процент всхожести.
- Итак, известные нам отношения: (Слайд 3)
Всхожесть = ![]() ;
; ![]() .
.
Значения данных отношений мы представляли в виде процентов.
III. Изучение нового материала.
Человеку часто приходится смешивать различные жидкости, порошки, вещества или разбавлять что-нибудь водой. При этом используют слово «концентрация». Как вы понимаете это слово?
В большом энциклопедическом словаре «концентрация (от новолат. concentratio) - сосредоточение, скапливание, собирание кого-либо, чего-либо в к.-л. месте» [1].
Концентрация в химии - величина, выражающая относительное количество данного компонента (независимой составной части) в физико-химической системе (смеси, растворе, сплаве) [2].
Сейчас разберемся с этим понятием с точки зрения математики. (Слайд 4)
Нальем в стакан 150 г воды и растворим в ней 50 г сахара. Какой станет масса раствора?[3]

50+150=200 (г) - масса общая. (Слайд 5)
Раствор тщательно перемешиваем.
Найдите процентное содержание сахара в растворе.
50 : 200=1: 4 = 0,25;
0,25=25%
25% - процентное содержание сахара в данном растворе.
Число 0,25 называют концентрацией сахара в растворе. (Слайд 6)
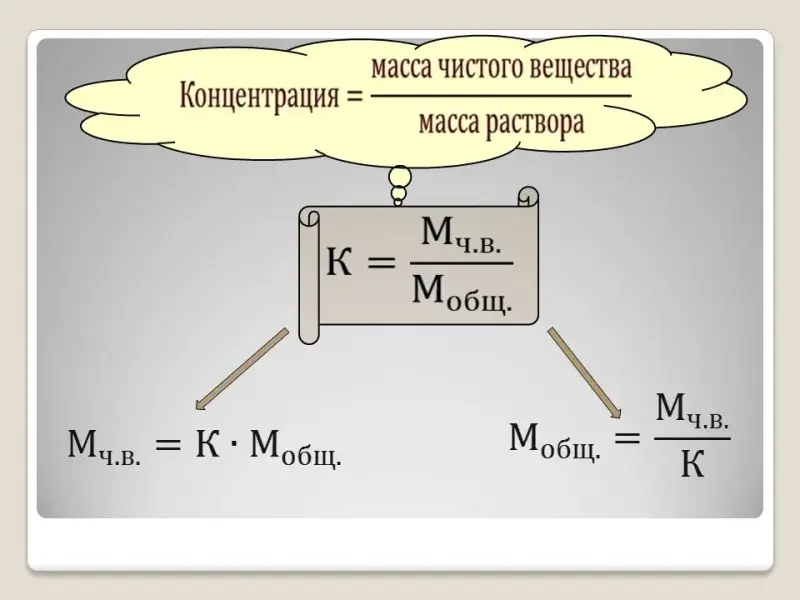
Итак, в математике, концентрацию можно представить как отношение чистого вещества к раствору (сплаву, смеси).
Концентрация = ![]() , т.е. К=
, т.е. К=![]() .
.
Как по этой формуле найти Мч.в? Мобщ?
Мч.в. = Мобщ · К
Мобщ = Мч.в: К
(Слайд 7)
IV. Решение задач на отработку формул:
(Слайд 8)
- В 500 г раствора содержится 100 г соли. Найдите концентрацию соли в данном растворе. Процентное содержание соли в растворе?
- 200 г раствора содержит 80% соли. Найдите массу соли в этом растворе.
- Какова масса раствора, в котором 150 г сахара составляют 25%.
Во многих текстовых задачах понятие «концентрация» может быть заменено на:[3] (Слайд 9-10)
| «жирность»
(масло, творог, молоко) |
 |
| «крепость»
(уксус) |
 |
| «соленость»
(морская вода, маринад) |
 |
| «влажность»
(в воздухе) |
 |
| «проба»
(в драгоценных металлах) |
 |
Рис.1.
Подумайте, отношение каких величин используется в понятиях «жирность, соленость, проба».
Встречая эти слова в текстах задач, вы должны понимать, что речь идет о «концентрации» того или другого чистого вещества в растворах или сплавах или смесях.
V. Физминутка.
(Слайд 11)
Следите глазами за движениями черепашек.
VI. Первичное закрепление нового материала.
Решим несколько задач на «концентрацию».
(Задачи 1-4 заранее распечатаны на листочке. (Приложение 1) Данные условий задач вносим в таблицу, обсуждаем ход решения. Отвечаем на вопросы к действиям.
Задача 1. В одну банку мама налила 480 г воды и насыпала 120 г сахара, в другую - 840 г воды и 160 г сахара. В какой банке вода слаще? [4] (Слайд 12-13)
Чтобы ответить на вопрос задачи, необходимо найти концентрации сахара в растворах каждой банки и сравнить их.
Решение:
-
Какова масса раствора в первой банке?
480+120 = 600 (г) -
Какова концентрация сахара в растворе первой банки?
120:600 = 0,2; 0,2=20% -
Какова масса раствора во второй банке?
840+160 = 1000(г) -
Какова концентрация сахара в растворе второй банки?
160:1000 = 0,16; 0,16=16% -
В какой банке вода слаще?
20% > 16%
Ответ: в первой банке вода слаще.
Задача 2. Смешивают 200 г 80%-го раствора соли и 700 г 20%-го раствора той же соли. Сколько соли в полученном растворе? (Слайд 14-15)
Решение:
80% - это процентное содержание соли в 200г раствора (концентрация 0,8)
- Сколько г соли в этом растворе?
0,8 ·200=160(г)
20% - это содержание соли в 700 г раствора (концентрация соли 0,2)
- Сколько г соли во втором растворе?
0,2·700=140 (г) - Сколько г соли в полученном растворе?
160+140=300 (г)
Ответ: 300 г.
Задача 3. Какой раствор получится при смешивании 200 г 50% раствора соли и раствора, в котором 150 г соли составляют 25%? (Слайд 16-17)
Решение:
50% - процентное содержание соли в 200 г растворе (концентрация 0,5).
-
Сколько г соли в этом растворе?
0,5·200=100 (г)
Что мы знаем про второй раствор? - Знаем количество соли (150г) и его процентное содержание25% (значит, концентрация соли 0,25) -
Какова масса второго раствора?
150:0,25= 600 (г)
Чтобы найти концентрацию соли в новом растворе, что надо знать? - Массу соли и массу всего раствора. -
Какова масса соли в двух растворах?
100+150=250 (г) -
Какова масса нового раствора?
200+600 =800 (г) -
Какова концентрация соли в новом растворе?
250:800=0,3125; 0,3125 = 31,25%
Ответ: 31,25%.
Задача для самостоятельного решения (дома).
Задача 4. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5%?[5]
Решение:
-
Сколько кг соли в морской воде?
0,05·30=1,5 (кг)
Пресная вода содержит соль? - Нет. - Значит, масса соли и в новом растворе будет 1,5 кг, но ее концентрация составит уже 0,015. -
Какова масса нового раствора (с добавлением пресной воды)?
1,5: 0,015= 100 (кг) -
Сколько пресной воды нужно добавить?
100 - 30 = 70 (кг)
Ответ: 70 кг.
VII. Этап рефлексии.
(Слайд 18)
Ответ на листочке:
- Сегодня я узнал….
- У меня получилось…
- Было трудно….
- Было интересно….
- Теперь я умею…
VIII. Итог урока. Домашнее задание.
(Слайд 19)
№754, 755, подготовить библиографическую справку о Магницком Л.Ф.; о его схеме решения задач на смеси, растворы.
Используемая литература:
- Большой энциклопедический словарь. -2-е изд., перераб.и доп. - М.:Большая Российская энциклопедия, 1998. - 1456 с.: ил.
- slovari. yandex.ru
- urok.1sept.ru/articles/520040
- Математика: учеб. для 6 кл. общеобразоват. учреждений/ [Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др.]; под ред. Г.В. Дорофеева, И.Ф. Шарыгина. - 8-е изд.-М.: Просвещение, 2006. - 302 с. :ил.
- Сборник задач по математике для поступающих во втузы (с решениями). В 2-х кн. Кн. 1. Алгебра: Учеб. пособие / В.К. Егерев, В.В. Зайцев, Б.А. Кордемский и др.; под ред. М.И. Сканави. - 7-е изд., перераб. и доп. - М.: Высш.шк., 1994. - 528 с.: ил.