"Воображаемый график", "Морской бой" и угловой коэффициент прямой

Шекспир.

Понятие функции – трудное. Процесс изучения функций можно облегчить, сделав акцент на наглядность, то есть активно использовать график. График становится тем письменным знаком, который содержит в себе информацию о самой функции. Но как добиться того, чтобы эта информация стала доступной для осмысления?

В заданиях, которые предлагают авторы учебников (например, [3]), на первый план выходят такие, где требуется определить некоторую числовую величину, связанную с данной функцией. Например, найти значение функции по заданному значению аргумента (и обратная задача), установить принадлежность точки графику, найти координаты точек пересечения двух графиков и др. Можно назвать такие задания задачами количественного характера. Но есть и другие: задачи качественного характера. Они предлагают, скажем, установить, в каких четвертях расположен график, сколько точек пересечения он имеет с другим графиком, какой формулой можно было бы задать функцию, графиком которой будет данная линия, и многое другое. Здесь не требуется детальных расчетов, но необходимо общее представление о графике и четкое знание основных свойств изучаемой функции. Такие задания тоже присутствуют в учебных пособиях, только их, к сожалению, гораздо меньше. Тем не менее, в работах по подготовке к ГИА и ЕГЭ они постоянно встречаются.

На своих уроках я стараюсь вводить как можно больше задач качественного характера. Для того, чтобы ученик лучше понимал особенности графика, я использую некоторые методические приемы, о двух из них и рассказывается в данной статье.

Важнейшая характеристика линейной функции у=kx+b – это угловой коэффициент, то есть коэффициент k.

Почему угловой коэффициент прямой называется именно угловым? Угол, с которым связан этот коэффициент, – это угол наклона прямой к положительному направлению оси абсцисс. Замечаем, что при k>0 график “уходит” вправо вверх, при k<0 – вправо вниз, при k=0 имеем горизонтальную прямую. Установить эти факты экспериментальным путем несложно, но слабые ученики достаточно быстро их забывают. Чтобы обнаруженная закономерность отложилась в памяти, ученикам предлагаются следующие упражнения. Видя формулу линейной функции, дети должны показать расположение прямой, определенным образом подняв свою руку, то есть используется “воображаемый график”.

Предварительно ученикам нужно посоветовать, как лучше это делать. Левую руку поднимаем так, чтобы локоть был примерно на уровне10-15см от поверхности стола, пальцы вытянуты по прямой вместе с кистью. Если прямая горизонтальна, то рука от локтя до кончиков пальцев – в горизонтальном положении, на уровне груди. Если k>0, то направляем кисть вверх, кончики пальцев указывают “вправо вверх”. Если k<0, то локоть приподнимается, а кисть опускается, кончики пальцев указывают “вправо вниз”. Главную роль играют кончики пальцев, именно они указывают нужное положение прямой.

Таким образом, на вопросы учителя дети отвечают, расположив нужным образом левую руку. Кто-то из учеников может прокомментировать, почему он выбрал определенное положение (исходя из данного в условии значения углового коэффициента).

Практика показывает, что учителю сразу хорошо видно, кто из учеников показывает верно, а кто нет. Единственно, что должен учесть учитель: ученики показывают “вправо” – для себя, а для человека, стоящего к ним лицом, – это направление “влево”. Но учитель быстро настраивается на эту смену направлений, ему только нужно обратить внимание детей, что они показывают “для себя”.

Такая “зарядка” активизирует весь класс, привнося эффект занимательности. С семиклассниками “постановка руки” вполне удается, и в дальнейшем “воображаеиый график” они показывают легко.

Какова результативность этих упражнений? У учащихся в памяти остаются прочные связи между знаком углового коэффициента и наклоном прямой. Параллельно с изучением этих связей ученики знакомятся с тем, что второй коэффициент линейной функции указывает нам точку на оси ординат, через которую проходит график. А зная точку и угол наклона прямой (острый, тупой или 0 градусов – прямая горизонтальна), можно схематично изобразить график линейной функции! Таким образом, мы получаем мощный инструмент для качественного анализа графиков линейных функций. Помимо решения новых задач, это нам поможет и для проверки обычных заданий на построение графиков линейных функций. Проверяем расположение прямой: какой у нее угловой коэффициент, как она проходит? Ведь из-за вычислительных ошибок при заполнении таблицы контрольных точек дети иногда проводят прямую совсем неверно, а знак углового коэффициента может дать корректировку.

Неоценима та роль, которую эти упражнения сыграют в девятом классе, при изучении основных свойств функции. При определении возрастания функции мы пользуемся, условно говоря, конструкцией “чем больше х, тем больше у”. Переходя к графику, мы увидим, что “чем правее х, тем выше у”. А направление кончиков пальцев в наших упражнениях при k>0 как раз и показывает “вправо вверх”. Аналогичные рассуждения можно провести для убывающей линейной функции.

При изучении графиков у=х², у=х³, у=, y = встречаются следующие трудности. Во-первых, сама форма линии (кривая!) вызывает у детей отчасти негативное отношение. Во-вторых, для построения графика по точкам требуется произвести гораздо больше расчетов, чем в случае линейной функции. Это достаточно утомительно для некоторых учеников. Но самое главное заключается в оценке конечного результата: у линейной функции график прямая, а прямая знакома каждому ребенку, но если график – кривая, то она сама по себе ничего семикласснику не говорит. Построив график, ученик может облегченно вздохнуть только потому, что закончилось это трудное занятие (он же начертил кривую!), не подозревая о том, что, возможно, у него на графике есть ошибки.

Поэтому для лучшего восприятия каждой кривой я указываю детям на ее особенности, которые мы видим на графике. По возможности выделяю на графике присущие ему отдельные элементы. Это необходимо для того, чтобы сделать данную линию более понятной ученику и чтобы в дальнейшем он узнавал эту кривую так же свободно, как и хорошо знакомую прямую.

Например, у параболы есть вершина и ветви. Ветви симметричны относительно оси ординат. При заполнении таблицы контрольных точек мы обращаем внимание на то, что квадраты противоположных чисел равны, но то, что это приводит нас к симметрии графика относительно оси ординат, лучше всего воспринимается при взгляде на саму параболу. У вершины замечаем “плавное” закругление, это замечание, связанное с понятием гладкости кривой, важно сделать уже сейчас, потому что распространена ошибка: дети в спешке стараются ветви параболы вытянуть вверх так, что вблизи вершины получается чуть ли не острый угол. Некоторые дети воспринимают параболу не как линию, а как плоскую фигуру (например, говорят, что она похожа на жука) и подсознательно стремятся “дорисовать” ее, направляя ветви во внутреннюю часть графика. Иногда ветви уходят в стороны так, что меняется характер выпуклости графика.

Учитель должен все эти ошибки спрогнозировать и подчеркнуть особенности параболы. Помимо обычного построения графика и его дальнейшей проверки я использую при этом прием “воображаемого графика”, то есть ученики по воздуху показывают форму параболы (или гиперболы и т.д.). Сначала они это делают вместе с учителем, который на основных моментах фокусирует их внимание. Здесь очень помогает “плавное”, неторопливое движение, к нему быстро привыкают даже слабые ученики, и они лучше запоминают сам график.

Рука показывает, начиная с левых участков графика, то есть мы все время двигаемся в направлении оси абсцисс слева направо, а график либо поднимается, либо опускается. Таким образом, мы опять с помощью этих упражнений можем рассуждать об участках возрастания или убывания функции. Ведь само понятие возрастания (убывания) психологически связано с некоторым процессом, движением: значения аргумента возрастают (по оси абсцисс “двигаемся” вправо), значения функции увеличиваются/уменьшаются (по оси ординат – вверх/вниз).

Упражнения, внешне похожие на описанные, давно применяются в начальной школе – это так называемое “воображаемое письмо”. Ученики обводят по воздуху контур буквы. “Именно жест есть первоначальный зрительный знак, в котором заключается…будущее письмо ребенка. Жест является письмом в воздухе, а письменный знак – очень часто просто закрепленным жестом”[1].

Но если в этом случае цель для первоклассника – правильно воспринять саму форму буквы, уметь ее воспроизвести и никакого дополнительного содержания, кроме обозначения конкретной буквы, в этом знаке нет, то для ученика средней школы график – это принципиально другой зрительный объект. Кроме того, что он непосредственно “указывает” на определенную функцию, он одновременно иллюстрирует ее важные свойства. И эти свойства ученику нужно научиться осмысленно воспринимать. “При осмысленном восприятии я вижу в предмете нечто большее, чем содержится в непосредственном зрительном акте, и восприятие предмета является уже в известной степени абстракцией и в восприятии содержатся следы обобщения”, – эти слова Л.С. Выготского [2] характеризуют общие психологические особенности восприятия, но они, в частности, прекрасно иллюстрируют процесс изучения графиков на уроках математики.

При осознании того, как выглядит график возрастающей (убывающей) функции, ученик быстрее поймет геометрический смысл производной и ему проще будет установить связь между характером монотонности функции и знаком производной. Это происходит потому, что расположение касательной и знак ее углового коэффициента – знакомые понятия для учащихся благодаря систематической работе по исследованию свойств линейной функции начиная с седьмого класса.

Выше были приведены упражнения, которые помогают определять знак углового коэффициента. Для вычисления его значения можно использовать разные приемы, мы остановимся на том, где главную роль играет геометрический подход.

Лучше всего при этом опираться на формулу , но ее можно ввести только в восьмом классе, когда в геометрии будет рассмотрено определение тангенса. С сильными учениками можно уже в седьмом классе рассмотреть формулу, использующую координаты двух точек, принадлежащих прямой: . Кроме формулы для вычисления углового коэффициента ученикам потребуется знание о соответственных углах при параллельных прямых. Таким образом, ученикам можно предложить новый способ построения графика линейной функции, а также определения углового коэффициента по готовому графику несколько позже, чем изучается сама линейная функция. Это можно сделать, например, в конце седьмого класса, когда рассматривается графический способ решения систем линейных уравнений. Или уже в восьмом классе, когда будет разобрано определение тангенса угла.

В предлагаемом способе мы активно используем чертежи на клетчатой бумаге.

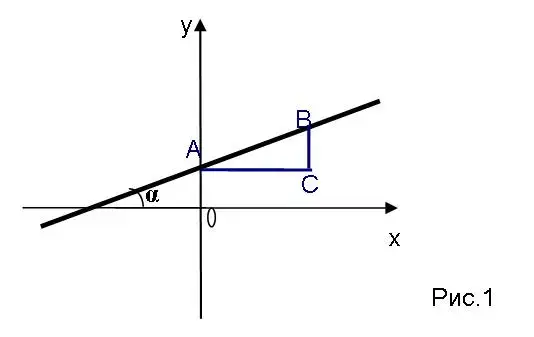
Итак, пусть задана линейная функция y=kx+b. График должен пройти через точку (0;b). Отметим эту точку в координатной плоскости, на рисунке она обозначена точкой А <Рисунок 1>. Допустим, что k>0. Значит, (угол наклона) – острый.  Покажем в воздухе, как должна пройти прямая (кончики пальцев направлены вправо вверх!). Строим прямоугольный треугольник АВС, у которого гипотенуза задает нам расположение нашей прямой, катеты параллельны осям координат, вершина одного острого угла совпадает с точкой А(0;b), и при этом tgA=tg, то есть tgA=k. Как это сделать? Если k – целое, то удобно выбрать АС=1, тогда ВC=k, и, значит, tgA=k. Если k – дробное, k=, то можно взять ВС = m, АС = n. Таким образом, мы нашли точку В – это вторая точка нашей прямой. Через А и В проводим прямую – это график нашей функции.

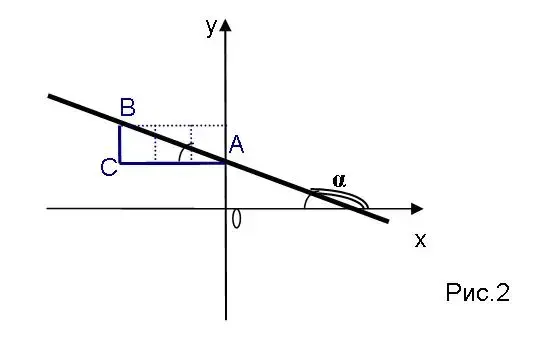
Если k<0, то рассуждения аналогичные, но не забываем, что угол наклона в данном случае тупой <Рисунок 2>. Кроме этого, замечаем, что tgA=tg(180^о – )= – tg = –k, причем –k >0. Например, если k =, то – k = и можно выбрать АС=3, и тогда ВС=1.

Часто встречаются задания, где или . Наш треугольник может быть получен из прямоугольника, напоминающего “кораблик” из игры “Морской бой”, в этом прямоугольнике нужно провести диагональ, гипотенузу будущего треугольника (не забывая про угол наклона!). Если значения k целые, то этот кораблик расположен вертикально (АС=1, а катет ВС равен 1, 2, 3 или 4). Если , то кораблик в горизонтальном положении (АС равен 2, 3 или 4, ВС=1). На рисунке 2 мы видим прямую с угловым коэффициентом , для ее построения по клеткам выбираем трехклеточный “кораблик” в горизонтальном положении, а его диагональ, то есть гипотенуза треугольника АВС, расположена так, что угол наклона прямой к Ох тупой (прямая будет идти “вправо вниз”). При определенной тренировке расположение треугольника угадывается быстро, и этому помогает практика в игре “Морской бой”. А также можно заранее решать с ребятами подготовительные задачи, которые предлагаются, например, в [4], в главе “Геометрия на клетчатой бумаге”.

Используя аналогичные рассуждения можно по готовому графику узнать угловой коэффициент прямой, если график изображен на клетчатой бумаге. Например, можно решить из учебника 7 класса[3]: №328, 329 и другие. А также многие задания из тренировочных работ по подготовке к ГИА и ЕГЭ. Обычно в условии мы встречаем такие данные, что все вершины треугольника можно расположить в узлах клеток, треугольник легко обнаруживается.

При должной тренировке у детей развивается глазомер и они могут отвечать на вопросы по чертежам, где клетки и не пропечатаны. Например, ученики быстро сравнивают различные графики линейных функций, замечая, например, что угловой коэффициент одной прямой больше, чем у другой, и первая прямая быстрее идет вверх, первая функция изменяется быстрее – это хорошая подготовительная работа для введения понятия производной в старшей школе. Кроме того, осмысленное восприятие графиков поможет детям лучше их анализировать на других уроках (в первую очередь, на уроках физики).

Рассмотренный геометрический подход повышает интерес к уроку и позволяет значительно сэкономить время: не нужно делать утомительных расчетов, нужно только рассуждать, внимательно рассматривая график – “глазами слушать”, о чем нам говорит функция.

Литература.

1. Выготский Л.С. История развития высших психических функций // Собрание сочинений: в 6 т. – М.: Педагогика, 1983. – Т.3.
2. Выготский Л.С. Вопросы детской (возрастной) психологии // Собрание сочинений: в 6 т. – М.: Педагогика, 1984. – Т.4.
3. Макарычев Ю.Н. и др. Алгебра. 7 класс. – М.: Просвещение, 2009.
4. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия – М.: МИРОС, 1995.