Конспект выступления по теме "Решение заданий С2 координатно-векторным методом"
I. Основные формулы:
1. Расстояние между точками А (![]() ,
, ![]() ), В
), В ![]() ,
, ![]() ) равно
) равно ![]() =
=![]() .
.
2. Угол между плоскостями. Если β - угол между плоскостями, заданными уравнениями ![]() х+
х+![]() z+
z+![]() =0 и
=0 и
![]() х+
х+![]() z+
z+![]() =0, то
=0, то
 .
.
3. Расстояние от точки до плоскости. Если ρ - расстояние от точки ![]() (
(![]() ,
, ![]() ), до плоскости
), до плоскости ![]() х+
х+![]() z+D =0, то
z+D =0, то
ρ=![]() .
.
4. Уравнение плоскости, проходящей через три заданные точки ![]() (
(![]() ,
, ![]() ),
),![]() (
(![]() ,
, ![]() ),
),![]() (
(![]() ,
, ![]() ), в координатной форме:
), в координатной форме:
 =0;
=0;
5. Если отрезок, концами которого служат точки А (![]() ,
, ![]() ), В
), В ![]() ,
, ![]() ) разделен точкой С (х, у,
) разделен точкой С (х, у,![]() ) в отношении λ, то координаты
точки С определяются по формулам
) в отношении λ, то координаты
точки С определяются по формулам
Х = ![]() ; у=
; у=![]() ; z=
; z=![]() .
.
II. Координаты вершин многогранников.
Определите координаты вершин многогранников:
1. Единичный куб A...D1

Решение: координаты вершин А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), D (0, 1, 0), D1 (0, 1, 1), С (1, 1, 0), С1 (1, 1, 1).
2. Правильная треугольная призма A…C1 , все ребра, которой равны 1.

Решение: координаты вершин: А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), С (0,5; ![]() , 0), С1 (0,5;
, 0), С1 (0,5; ![]() , 1).
, 1).
3. Правильная шестиугольная призма A...F1, все ребра которой равны 1.

Решение: координаты вершин: А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), С (1,5; ![]() , 0), С1 (1,5;
, 0), С1 (1,5; ![]() , 1), D (1,
, 1), D (1, ![]() (1,
(1, ![]() Е (0,
Е (0, ![]() ,
, ![]() (0,
(0, ![]() ,
,
F(-0,5 , ![]() 0),
0), ![]() (-0,5,
(-0,5, ![]() 1).
1).
4. Правильная треугольная пирамида (тетраэдр) ABCD все ребра которой равны 1.

Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (0,5; ![]() , 0), D (0,5,
, 0), D (0,5,
![]()
5. Правильная четырехугольная пирамида SABCD, все ребра которой равны 1.

Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (1, 1, 0), D (0, 1, 0![]() S (0,5; 0,5;
S (0,5; 0,5;
![]() ).
).
6. Правильная шестиугольная пирамида SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2.

III. Решение задач.
Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (1,5; ![]() , 0), D
(1,
, 0), D
(1, ![]() Е (0,
Е (0, ![]() , F
(-05,
, F
(-05, ![]() 0), S (0,5;
0), S (0,5; ![]() ).
).
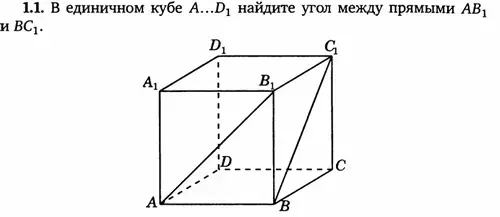
Решение:
- А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), D (0, 1, 0), D1 (0, 1, 1), С (1, 1, 0), С1 (1, 1, 1).
- Найдем координаты векторов
 (1, 0, 1) и
(1, 0, 1) и  = (0, 1, 1)
= (0, 1, 1) - Найдем косинус угла между векторами
 =
= =
= ; α=60.
; α=60.
Ответ: 60.
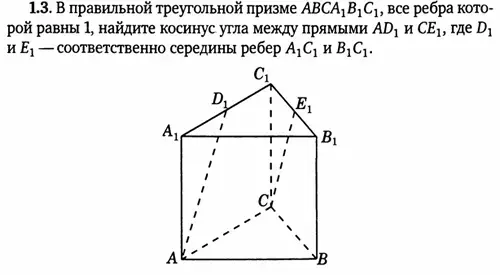
Решение:
- координаты вершин А (0, 0, 0), D1 (
 ,
,  , 1), С (0,5;
, 1), С (0,5;  , 0), Е1
(
, 0), Е1
( ;
;  ,
1).
,
1). - Найдем координаты векторов:
 и
и 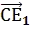 (
( ,
, 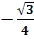 , 1)
, 1) - Найдем косинус угла между векторами
 =
=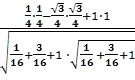 =0,7;
=0,7;
Ответ: 0,7.
Полностью текст работы приведен в Приложении.