Урок математики "Разложение чисел на простые множители"
Тема урока: «Разложение чисел на простые множители».
Цель урока: выработать навык разложения чисел на простые множители, повторить признаки делимости чисел и использовать их при разложении чисел на простые множители, продолжать расширять представления учащихся об окружающем их мире.
ХОД УРОКА
Учитель: Добрый день, ребята. Садитесь. Откройте тетради и запишите число, классная работа. Тема нашего урока «Разложение чисел на простые множители».
Давайте вспомним, что это значит? Какие числа являются простыми? Какие еще вы знаете числа? К какой группе относится число 1? Теперь мы повторим, изученные нами, признаки делимости чисел на 3, 9, 5,
2 и 10. (Фронтально)
1) Работа в парах. Задание учащимся: заполнить таблицу:
|
Кратно10 |
Кратно 9 |
Кратно 3 |
Кратно 3 и 5 |
Кратно 2 |
Кратно 9 |
Кратно 2 и 9 |
|
| Число | |||||||
| Буква |
«ш» 312 «ч» 310
«е» 567 «в» 585
«ы» 555 «б» 771
Ответ:
|
Кратно10 |
Кратно 9 |
Кратно 3 |
Кратно 3 и 5 |
Кратно 2 и 3 |
Кратно 9 |
Кратно 5 и 9 |
|
| Число |
310 |
567 |
771 |
555 |
312 |
567 |
585 |
| Буква |
ч |
е |
б |
ы |
ш |
е |
в |
Историческая справка: Пафнутий Львович Чебышев - русский математик. Он занимался изучением свойств простых чисел. Он доказал, что между любым натуральным числом, большим 1, и числом, вдвое большим, всегда имеется не менее одного простого числа. Давайте проверим это на примере нескольких чисел. (Устно)
2) Задание учащимся: Соедините стрелками равные выражения, предварительно разложив числа из левого столбика на простые множители.
На доске записано:
125 2 . 2 . 2 . 2 . 7
315 5 . 5 . 5
444 2 . 2 . 3 . 13
112 2 . 2 . 3 . 37
156 3 . 3 . 5 . 7
Как по-другому можно записать выражения, стоящие в правом столбике?
24 . 7, 53, 22 . 3 . 13, 22 . 3 . 37, 32 . 5 . 7.
2) Проверьте правильность разложения чисел на простые множители, поставив знаки «+» или «-».
3) Задание учащимся: из чисел 84, 44, 75, 60 выберите то, которое раскладывается на наибольшее количество простых множителей. Подчеркните это число зеленым цветом.
4) Работа по группам
Задание учащимся: по разложениям чисел определите, какие из них делятся на 2, на 3, на 4, на 6, на 7:
- 2 . 11 . 13
- 2 . 5 . 3 . 17
- 3 . 5 . 23 . 41
- 2 . 2 . 2 . 3 . 7.
Выпишите отдельно разложения чисел, делящихся: на число 4; на число 6.
5) Отвечая на вопросы, впишите верные слова и в выделенном столбце получите имя ученого, математика, жившего до нашей эры.
1. Продолжите предложение: натуральное число, имеющее только два делителя называется …
2. Как называется натуральное число, на которое число а делится без остатка?
3. Какое число является делителем любого натурального числа?
4. Назовите автора первого учебника по математике.
5. Продолжите предложение: натуральное число, имеющее более двух делителей, называется …
6. Как называются числа, используемые при счете?
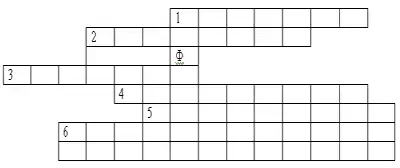
Ответы:
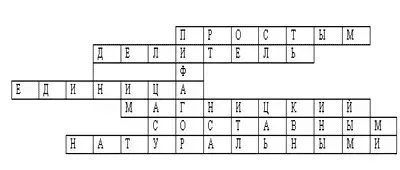
В данном кроссворде «спрятано» имя Пифагора Самосского (VI в. до н.э.). Историческая справка на эту тему: Пифагор и его ученики изучали вопросы делимости чисел. Число, равное сумме всех его делителей (без самого числа), они называли совершенным числом. Например, 6 = 1 + 2 + 3; 28 = 1 + 2 + 4 + 7 + 14; 496; 8 128.
Подведение итогов урока: Давайте подведем небольшой итог. Какова была цель урока? Мы её достигли?
Домашнее задание: п.41, № 495(3), №503, №507 (2).