Математический КВН. Внеклассное мероприятие для учащихся 7-х классов
Предмет математики настолько серьёзен, что нужно не упускать случая, делать его немного занимательным.
Б.Паскаль
Цели и задачи: активизировать мыслительную деятельность учащихся, развивать внимание, наблюдательность, память, речь, быстроту реакции, повышать интерес к изучаемому предмету, способствовать развитию, коммуникативных способностей учащихся, созданию атмосферы взаимовыручки.
Предварительная организация игры:
(За две недели до игры, каждый класс получает приглашение для участия в КВН).
Приглашаем принять участие в игре "Математический КВН".
Участники игры:
- Команда учащихся 7 "А" (12 человек)
- Команда учащихся 7 "Б" (12 человек)
Необходимо создать команды, выбрать капитана команды.
Командам приготовиться по следующим позициям:
1. Визитная карточка. Максимальная оценка -5 баллов.
Команда должна представить себя.
Учитывается эмблема, название, внешний вид, девиз команды.
Условие: в названии и девизе должна просматриваться математическая тематика. Время выступления на сцене - 2 мин.
2. Разминка. Максимальная оценка -10 баллов.
Команда отвечает на вопросы ведущего. Вопросы из истории математики, программного материала, занимательной математики.
3. Конкурс капитанов. Максимальная оценка - 5 баллов.
4. Блиц турнир. Командам будут предложены вопросы. В течение 2 мин команды отвечают на них, за каждый правильный ответ команда получает 0,5 балла.
5. Разгадай кроссворд. Максимальная оценка - 5 баллов. Время разгадывания кроссворда - 3 мин.
6. Конкурс "Домашнее задание". Максимальная оценка - 20 баллов
Выступление на тему: "Математика и мы". Время выступления - 5 мин
Жюри оценивает интеллект, юмор, артистичность, убедительность, находчивость.
Желаем победы!
Оргкомитет игры "Математический КВН"
Разминка (вопросы задаются вслух командам поочередно).
1-й команде:
1. Индийцы называли его "сунья", арабские математики "сифр". Как мы называем его сейчас? Ответ: нуль
2. Именно этот учебник был первой в России энциклопедией математических знаний. По нему учился М.В.Ломоносов, называвший его "вратами учености". Именно в нем впервые на русском языке введены понятия "частное", "произведение", "делитель". Назовите учебник и его автора. Ответ: "Арифметика" Л.Ф.Магницкого
3. Это название происходит от двух латинских слов "дважды" и "секу", буквально "рассекающая на две части". О чем идет речь? Ответ: о биссектрисе
4. Кому принадлежат слова: "Математик должен быть поэтом в душе"? Ответ: С.В.Ковалевской
5. В древности такого термина не было. Его ввел в XVII веке французский математик Франсуа Виет. В переводе с латинского он означает "спица колеса" что это? Ответ: радиус
2-й команде:
1. "…природа формулирует свои законы языком математики". Кому принадлежат эти слова? Ответ: Г.Галилей
2. На могиле этого великого математика был установлен памятник с изображением шара и описанного около него цилиндра. Почти спустя 200 лет по этому чертежу нашли его могилу. Кто этот математик? Ответ: Архимед
3. Точка, от которой в Венгрии отсчитывают расстояния, отмечена особо. В этом месте в центре Будапешта стоит памятный знак. Кто или что было удостоено таких почестей? Ответ: нуль
4. Слово в переводе с греческого означает "натянутая тетива". Что это? Ответ: гипотенуза
5. Мы, в отличие от египтян, римлян и славян, пользуемся позиционной системой счисления, в которой всего десять цифр и "ступеньки". Что это за "ступеньки", перечислите их. Ответ: это разряды, их всего три - единицы, десятки, сотни
Конкурс капитанов.
1. Найдите ошибку в следующих рассуждениях:
Имеем верное числовое равенство 4:4=5:5. Вынесем за скобки в каждой части общий множитель. Получим 4(1:1)=5(1:1). Числа в скобках равны, поэтому 4=5 или 2*2=5.
2. Найдите ошибку в следующих рассуждениях:
Рассмотрим верное числовое равенство 35+10-45=42+12-54
Вынесем общие множители левой и правой частей за скобки. Получим: 5(6+2-9)=6(7+2-9). Разделим обе части этого равенства на общий множитель, заключенный в скобки. Получаем 5=6. В чем ошибка?
Блиц-турнир.
1-й команде:
| Вопросы: | Ответы: |
| 1. Результат сложения | сумма |
| 2. Сколько цифр вы знаете? | десять |
| 3. Как называется первая координата точки? | абсцисса |
| 4. Сотая часть числа | процент |
| 5. Прибор для измерения углов | транспортир |
| 6. Сколько сантиметров в метре? | сто |
| 7. Результат деления | частное |
| 8. В каком европейском городе есть улицы Пифагора, Архимеда, Ньютона и Коперника? | в Амстердаме |
| 9. Величина прямого угла | 900 |
| 10. Когда произведение равно нулю? | хотя бы один из множителей равен 0 |
| 11. Число, обращающее уравнение в верное равенство | корень уравнения |
| 12. Сколько сантиметров составляет 1% метра? | 1 см |
| 13. Отрезок, соединяющий точку окружности с ее центром | радиус |
| 14. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны | медиана |
| 15. Множество точек пространства, равноудаленных от данной точки | сфера |
| 16. Утверждение, требующее доказательства | теорема |
| 17. Цифровая оценка успехов | балл |
| 18. Прямые, не пересекающиеся на плоскости | параллельные |
| 19. Угол, смежный с углом треугольника при данной вершине | внешний угол |
| 20. Прямоугольник, у которого все стороны равны | квадрат |
| 21. Мера веса драгоценных камней | карат |
| 22. Угол, меньше прямого | острый |
| 23. Радиус окружности 6 см. чему равен диаметр? | 12см |
| 24. Сколько нулей в записи числа миллион? | шесть |
| 25. Какой знак надо поставить между двойкой и тройкой, чтобы получилось число больше 2 и меньше 3? | запятая |
| 26. Может ли угол параллелограмма быть равен 2000? | нет |
| 27. Третья буква греческого алфавита | гамма |
2-й команде:
| Вопросы: | Ответы: |
| 1. Результат вычитания | разность |
| 2. На какое число нельзя делить? | на 0 |
| 3. Как называется вторая координата точки | ордината |
| 4. Прибор для построения окружности | циркуль |
| 5. Сколько граммов в килограмме? | тысяча |
| 6. Наука, изучающая свойства фигур на плоскости | планиметрия |
| 7. Результат умножения | произведение |
| 8. Автор книги "Начала" | Евклид |
| 9. Величина развернутого угла | 1800 |
| 10. Когда частное равно нулю? | если делимое равно 0 |
| 11. Какую часть минуты составляют 15 секунд? | 1/4 |
| 12. Найдите 10% тонны | 100 кг |
| 13. Отрезок, соединяющий любые две точки окружности | хорда |
| 14. Утверждение, не вызывающее сомнений | аксиома |
| 15. Большая сторона в прямоугольном треугольнике | гипотенуза |
| 16. График линейной функции | прямая |
| 17. Сумма длин всех сторон многоугольника | периметр |
| 18. Ромб, у которого все углы прямые | квадрат |
| 19. Самая большая хорда в круге | диаметр |
| 20. Простейшее геометрическое понятие | точка |
| 21. Часть прямой, ограниченная с одной стороны | луч |
| 22. Сколько нулей в записи числа миллиард? | девять |
| 23. Диаметр окружности 8 м. Чему равен радиус? | 4 м |
| 24. Вид местности, открывающийся с возвышенного места | панорама |
| 25. Прибор для измерения углов на местности | астролябия? |
| 26. Чему равна сумма углов параллелограмма? | 3600 |
| 27. Масса 1 м3 воды | 1 тонна |
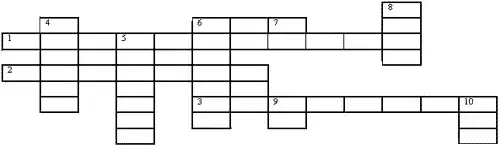
Разгадай кроссворд.
По горизонтали:
1. Числовой множитель
2. Утверждение, требующее доказательства
3. Многоугольник
По вертикали:
4. Значение переменной, обращающее уравнение в верное числовое равенство
5. Равенство, содержащее числа и переменные
6. Хорда, проходящая через центр
7. Международная система единиц
8. Единица измерения длины
9. Единица измерения площади
10. Американская единица измерения расстояния
Домашнее задание. Выступление на тему "Математика и мы".
Жюри подводит итоги.
Возможный вариант выступления команды (домашнее задание):
(На сцене стоит стол, вокруг которого расставлены 10 стульев)
Ведущий. 10 друзей, решив отпраздновать окончание средней школы в ресторане, заспорили у стола о том, как усесться вокруг него.
Первый друг. Давайте сядем в алфавитном порядке, тогда никому не будет обидно.
Второй. Нет, сядем по возрасту.
Третий. Нет, нет. Сядем по успеваемости.
Четвертый. Да ну, опять успеваемость, это вам не школа, да и надоело.
Пятый. Тогда я предлагаю сесть по росту, и никаких проблем.
Шестой. Устроим здесь физкультуру не так ли?
Седьмой. Придется тащить жребий.
Восьмой. Ну уж нет.
Девятый. По-моему уже обед остыл.
Десятый. Я сажусь, где придется, и вы, давайте за мной.
Появляется официант. Вы еще не расселись? Молодые друзья мои, оставьте ваши пререкания, сядьте за стол, как кому придется, и выслушайте меня.
(Все сели как попало).
Официант. Пусть один из вас запишет, в каком порядке вы сейчас сидите. Завтра вы снова явитесь сюда пообедать и разместитесь уже в ином порядке. Послезавтра сядете опять по иному и т.д., пока не перепробуете все возможные размещения. Когда же придет черед вновь сесть так, как сидите сегодня, тогда - обещаю торжественно - я начну ежедневно угощать вас всех бесплатно самыми изысканными обедами.
Друзья. Вот здорово, будем каждый день обедать у вас.
Ведущий. Друзьям не пришлось дождаться того дня, когда они стали питаться бесплатно. И не потому, что официант не исполнил обещания, а потому что число всех возможных размещений за столом чересчур велико. Оно равняется ни мало, ни много -3 628 800. такое число дней составляет, как нетрудно сосчитать, почти 10 000 лет! Вам может показаться невероятным, чтобы 10 человек могли размещаться таким большим числом различных способов. Но это действительно так. И в этом убедиться нам помогает математика.
Все исполняют песню:
В тот час, когда создатель
Все создавал вокруг,
Он создал математику -
Царицу всех наук.
И игреки, и иксы.
Шагают дружно в ряд
И дружною толпой они нас веселят.
И коль на жизненном пути
Не повезет, мой друг,
Ты вспомни математику -
Царицу всех наук.
На рынке и в спортзале
Нам нужен чисел ряд.
И пусть они тебя повеселят.