Обобщающий урок по теме: "Тригонометрические функции, их свойства и графики". 10-й класс
Цели:
- Развитие познавательного интереса к обучению.
- Применение математического моделирования как способа активизации аналитического мышления.
- Формирование практических навыков построения графиков функций на основе изученного теоретического материала.
Задачи:
- Использовать имеющийся потенциал знаний о свойствах функций в конкретных ситуациях.
- Уметь отстаивать свою точку зрения.
- Применять осознанное установление связей между аналитической и геометрической моделями тригонометрических функций.
Ход урока.
1. Организационный момент.
2. «Вход в урок».
На доске написаны 3 утверждения:
1) Тригонометрические уравнения sin x = a, cos x = a, tg x = a, ctg x = a всегда имеют решения.
2) График тригонометрической функции у = f(-x) можно получить из графика функции у = f(x) только с помощью преобразования симметрии относительно оси Оу.
3) График гармонического колебания можно построить, используя одну главную полуволну.
Учащиеся обсуждают в парах: верны ли утверждения? (1 минута). Затем результаты первоначального обсуждения (да, нет) вносятся в таблицу в столбец «До».
| Утверждение | До | После |
| 1 | ||
| 2 | ||
| 3 |
Учитель ставит цели и задачи урока.
3. Устные упражнения (фронтально).
1) Проверьте, принадлежат ли точки графикам функций:
у = sin x точка с координатами![]()
у = cos x точка с координатами ![]() .
.
2) Найти наибольшее и наименьшее значения функций:
у = sin x на отрезке ![]()
у = cos x на полуинтервале ![]()
у = tg х на полуинтервале![]()
3) Решите уравнения: cos x = 0, tg х = -1, sin x = 2.
4) Является ли число 15? периодом функций: у = sin x, у = cos x, у = tg х?
Назовите основной период этих функций.
5) Используя рисунки 14-17 на странице 38 задачника, составить аналитические модели функций по графикам.
4. Разминка (самостоятельно, с проверкой за доской).
№ 216(б). Решите графически уравнение sin x + cos x = 0.
5. Практическая работа № 1 (работа на заготовленных макетах в 4 группах, группы составлены по уровню подготовленности учащихся).
1 группа. № 210 (г). Сколько решений имеет система уравнений 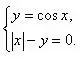
2 группа. № 183 (б). Решите графически уравнение sin x = х2 + 1.
3 группа. № 209 (в). Решите графически уравнение ![]()
4 группа. Сколько решений имеет уравнение sin 2x = tg х на отрезке ![]()
(Проверка и обсуждение по макетам).
Практическая работа № 2 (самостоятельная работа на листочках, 4 варианта, задания составлены по уровню подготовленности учащихся).
Построить график функции:
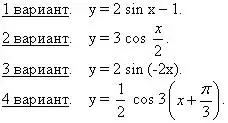
7. Обобщение и подведение итогов.
№ 194 (б,в). Постройте и прочитайте график функции у = f(x), где
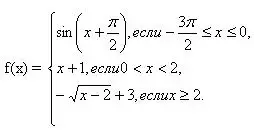
8. Итог урока. Возвращаемся к утверждениям (начало урока), обсуждаем, используя свойства тригонометрических функций, и заполняем в таблице столбец «После».