Цели урока:
- Образовательные: создать организационные и содержательные условия для формирования умений решения комбинаторных задач методом перебора возможных вариантов решения геометрическим способом (дерево решений), с применением правила умножения;
- Развивающие: развитие логического мышления, умений анализировать, сравнивать, сопоставлять, делать выводы;
- Воспитательные:
- Владение интеллектуальными умениями и мыслительными операциями.
- Воспитание трудолюбия, целеустремленности, положительного отношения к предмету.
Используемые технологии: технология коллективного взаимодействия, информационно-коммуникационные технологии, проблемное обучение.
Используемые методы: словесные, наглядно-иллюстративные, частично-поисковый, побуждающий диалог, подводящий к гипотезам диалог, организация самостоятельной исследовательской деятельности, выведение алгоритма.
Формы работы: фронтальная, самостоятельная, работа в группе.
Прогнозируемый результат (формируемые УУД)
Предметные:
- Получат представление о комбинаторных задачах, перебое все возможных вариантов решения, о дереве возможных вариантов, о правиле умножения.
- Уметь решать простейшие комбинаторные задачи с перебором всех возможных вариантов, с применением правила умножения.
Познавательные:
- Умение анализировать объекты, сравнивать, сопоставлять, устанавливать взаимосвязь объектов, делать выводы, составлять логическую цепочку рассуждений, создавать схемы и модели задачи.
Регулятивные:
- Умение строить логическую цепочку рассуждений, включая установление причинно-следственных связей.
Коммуникатиные:
- Уметь вести диалог на основе взаимного уважения. Уметь высказывать и обосновывать своё мнение, учитывать мнение других при поиске решения.
Личностные:
- Формирование устойчивых эстетических предпочтений, способности к эмоциональному восприятию материала, положительного отношения к учению, к предмету.
Средства обучения:
- ПК, интерактивная доска, презентация к уроку.
- Пакеты с индивидуальными и групповыми заданиями.
| Этап урока | Действия учителя | Действия учащихся | Формируемые УУД |
| 1. Самоопределение к учебной
деятельности. Орг.момент. Цель: создание атмосферы мотивации к уроку. |
Учитель приветствует учащихся, контролирует подготовленность к уроку. | Проверяют готовность к уроку. | Регулятивные: саморегуляция, самоконтроль. |
| 2. Введение в тему, актуализация
знаний и фиксация затруднений. Проблемная
ситуация. Цель: создать проблемную ситуацию, зафиксировать причину затруднений, спрогнозировать предстоящую деятельность. |
Вступление учителя: Задачи такого типа
мы решали в 5 классе. Встречались они и в этом
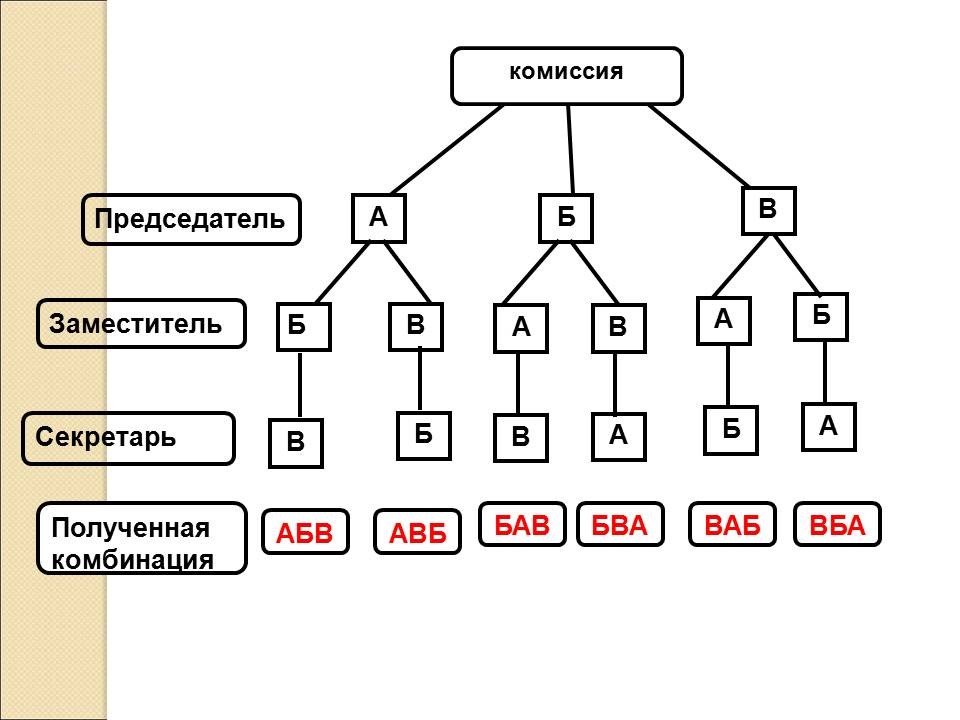
учебном году. Решите задачу № 492 самостоятельно. Собрание для проведения тайного голосования во важному вопросу избрало счетную комиссию, в состав которой вошли Антонов, Борисова и Ващенко. Члены счётной комиссии должны распределить обязанности: председатель, заместитель, секретарь. Сколькими способами они могут это сделать? Решение обсуждается и анализируется: Сколько вариантов выбора у вас получилось? Можно ли найти другие варианты? Учитель подводит итог обсуждение, вводит понятие комбинации и комбинаторных задач. |
Самостоятельное решение задачи № 492:
читают задачу, обдумывают решение, записывают
полученные варианты.
Озвучивают полученное решение, участвуют в обсуждении полученного результата. |
Познавательные (поиск нужной
информации, умение анализировать условие,
устанавливать причинно-следственные связи,
выстраивать логическую цепочку); Коммуникативные (умение вести диалог, учитывать разные мнения в сотрудничестве) Личностные (формирование способности к эмоциональному восприятию материала) Регулятивные (способность к самооценке) |
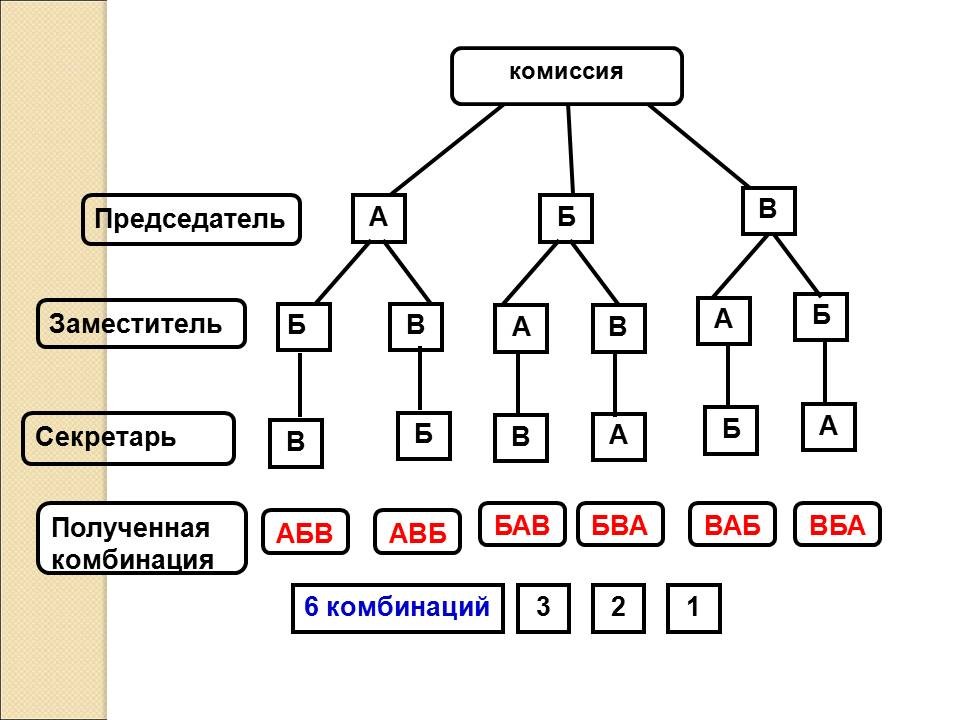
| Итак, перебором мы получили 6 вариантов
решения. Такие варианты перебора называются
комбинациями. А задачи, решаемые путем перебора
возможных вариантов, называются комбинаторными. Слово “комбинаторика” происходит от латинского combino – соединяю. Как вы считаете, может ли помочь комбинаторика в повседневной жизни, часто ли нам приходиться делать выбор между разными вариантами? Приведите пример такого выбора дома, в классе и т.п. Учитель сообщает, что комбинаторика – это раздел математики, с историей которого учащимся предлагается познакомится. Одним из учащихся представляется учебный проект по данной теме. |
Высказывают свое мнение, обосновывают
его. Приводят примеры из повседневной жизни
(выбор одежды на день, выбор меню, выбор дежурных
в классе и т.п.) Выступление одного из учащихся с учебным проектом по теме “История комбинаторики” |
||
| Учитель сообщает, что, кроме перебора
возможных комбинаций, комбинаторные задачи
решались с помощью геометрической модели. Вместе
с учащимися строят такую модель.Учащимся
предлагается вспомнить название такой
геометрической модели. В качест-ве подсказки им
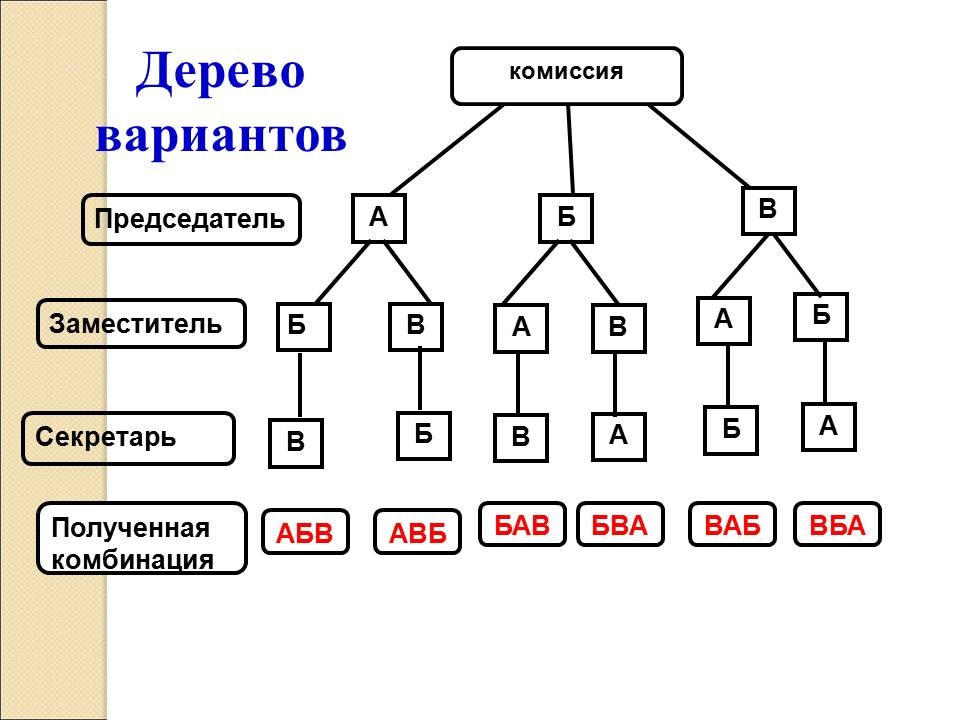
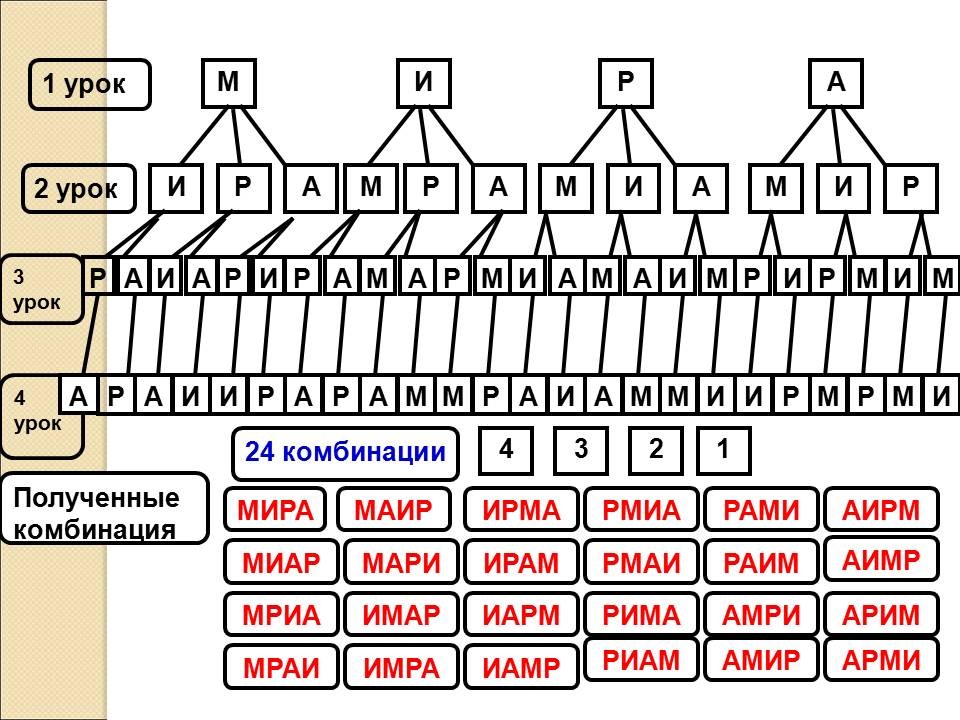
предлагается загадка: Его весной и летом Составленная геометрическая модель задачи называется деревом вариантов. |
В сотрудничестве с учителем строят геометрическую модель задачи – дерево вариантов. | ||
| 3. Постановка учебной задачи. Цель: обсуждение затруднений, построение проекта выхода из затруднения, проговаривание темы и целей урока. |
Учащимся предлагается побыть несколько
минут в роли завуча школы и решить ещё одну
задачу (№ 977 учебник Зубарева И.И. “Математика 5
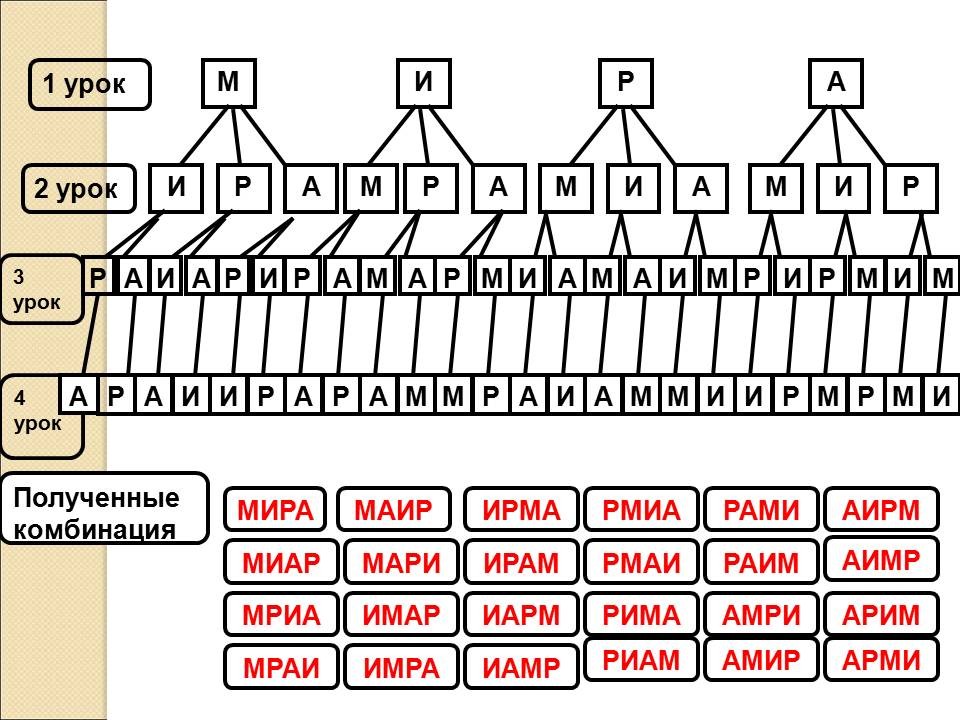
класс”) В 5 “А” классе в среду 4 урока: математика, информатика, русский язык, английский язык. Сколько можно составить вариантов расписания на среду? |
Групповая работа. Используют заранее заготовленные бланки расписания. На работу выделяяется ограниченное время. | Познавательные (самостоятельно выделять познавательную цель, умение анализировать условие, устанавливать причинноследственные связи, выстраивать логическую цепочку); Коммуникативные (умение вести диалог, высказывать и обосновывать свое мнение, учитывать разные мнения в сотрудничестве) Личностные (критичность мышления) - Регулятивные (прогнозирование) |
| Решение обсуждается: сколько вариантов
выбора успели найти? Все ли возможные варианты
решения найдены? Сколько всего возможных
вариантов решения задачи? Как проверить полноту
решения? Составляется дерево вариантов. Фронтальная проверка решения. Дерево вариантов, составленное для решения задачи, получилось достаточно громоздким. Представьте, что завучу школы приходится составлять расписание для каждого класса из 6-7 уроков. Удобным ли в таком случае будет геометрический способ для поиска всех возможных вариантов? Вернемся к решению задач. Учитель предлагает учащимся ответить на вопросы: |
Участвуют в обсуждении решения,
предлагают для проверки составить дерево
вариантов. Групповая работа. |
||
| Сколько вариантов выбора председателя
комиссии, заместителя, секретаря каково общее
число вариантов? Как могут быть связаны эти
величины? Сколько вариантов выбора можно указать для 1 урока? Для второго? Для третьего? Для четвертого? Каково общее число вариантов? Как могут быть связаны эти величины? |
Отвечают на вопросы учителя, анализируют решение, выдвигают свои гипотезы о взаимосвязи величин. | ||
| Итак, о решении каких задач мы говорим
на сегодняшнем уроке? С помощью какого правила
можно найти общее число решений комбинаторных
задач? Сформулируйте тему урока и его цели. Тема “Правило умножения для комбинаторных задач” Цель: сформулировать правило умножения решения комбинаторных задач, научиться применять его. |
Предлагают формулировки темы и целей урока. Уточняют, записывают тему. | ||
| 4. Реализация построенного
знания. Открытие нового знания. Цель: фиксация нового знания в речи и знаково. |
Задача 507: В 6 “А” классе в пятницу 6 уроков: математика, информатика, русский язык, английский язык, история, физкультура. Сколько всего можно составить вариантов расписания на пятницу? Сколько времени потратит завуч на запись всех вариантов, если известно, что на запись одного варианта у него уходит 30 секунд? |
Самостоятельно решают задачу. | Познавательные (поиск нужной
информации, умение анализировать условие,
логическую цепочку); Коммуникативные (умение вести диалог, учитывать разные мнения в сотрудничестве) Личностные (критичность мышления) Регулятивные (самоанализ, самооценка) |
| Ответьте на первый вопрос задачи, не
составляя графическую модель. Используйте в
решении правило умножения. Решение: 6*5*4*3*2*1 = 720 Объясните приведенное решение. Как вы рассуждали? Затем учитель предлагает учащимся сформулировать правило умножения решения комбинаторных задач. Мнения учащихся обсуждаются, правило уточняется и фиксируется в устной речи. |
Участвуют в обсуждении найденного решения. Предлагают свои варианты правила умножения. Уточняют, фиксируют в устной и письменной форме. | ||
| Физкультминутка. | |||
| 5. Первичное закрепление с
комментированием во внешней речи. Цель: развивать умения применять новые знания в типовых заданиях. |
Закончите решение задачи № 507. Ответьте
на второй вопрос задачи, выразив результат в
часах. № 495 Несколько стран решили использовать для своего государственно флага символику в виде трех горизонтальных полос одинаковой ширины разных цветов: белого, синего и красного. Сколько стран могут использовать такую символику при условии, что у каждой страны свой флаг? |
Самостоятельное решение задач. Фронтальная проверка решения. | Познавательные (умение
устанавливать взаимосвязь объектов); Коммуникативные (умение вести диалог) |
| Решите задачу, выполнив рисунки.
Проверьте полноту решения с помощью правила
умножения. 3*2*1=6 Есть ли среди полученных флагов известные вам? Действительно, один из флагов – флаг России. С другими нас познакомит ещё один учебный проект. |
Выступление одного из учащихся с учебным проектом по теме “Комбинаторика и флаги мира” | ||
| 6. Самостоятельная работа с
самопро-веркой по эталону. Цель: самопроверка умения применять новое знание в типовых условиях |
Решите задачу по правилу умножения № 494 Сколько трехзначных чисел можно составить из цифр 1, 3, 5, 7? Сколько трехзначных чисел можно составить из цифр 1, 3, 5, 7, при условии, что цифры не должны повторяться? Проверьте свое решение, сравнив его с приведенным в учебнике. Все ли выполнили верно? Где были допущены ошибки в решении? Какое условие не учли в решении? |
Самостоятельное решение задачи. Проверяют решение по заданному эталону в учебнике. | Познавательные (самостоятельный
выбор действия в соответствии с поставленной
задачей); Коммуникативные (рефлексия своих действий) Личностные (ответственное отношение к учению) - Регулятивные (действовать с учетом выделенных ориентиров) |
| Самостоятельная работа в группах № 501-505 | Самостоятельная работа в группах | ||
| 7. Рефлексия учебной деятельности на
уроке. Цели: соотнесение цели урока и его результатов, самооценка работы на уроке, осознание метода построения нового знания. |
Итак, сегодня, вы познакомились еще с
одним способом решения комбинаторных задач:
использование правила умножения для подсчета
возможных вариантов. Давайте сравним известные вам способы решения комбинаторных задач. В чем “плюсы” каждого из способов? В чем недостатки? Поэтому для каждой конкретной задачи нужно выбирать наиболее удобный способ решения. |
Отвечают на вопросы учителя.
Обосновывают ответы с опорой на новые знания и
умения. Самооценка того, что должно было быть усвоено и что усвоено самим учеником. |
Познавательные (осознанное вла-дение
способами решения); Коммуникативные (строить точное высказывание, аргументировать свою позицию) - Регулятивные (способность к самооценке) |
| 8. Домашнее задание. | № 496, 506. Творческое задание: составить комбинаторную задачу. |
Записывают домашнее задание. |
Список использованных ЭОР.
- Единая коллекция Цифровых Образовательных
Ресурсов, учебные и методические материалы к
учебнику “Математика 6” Зубаревой И.И.,
презентация “Правило умножения для
комбинаторных задач http://school-collection.edu.ru/catalog/res/581bf6ad-b670-4aa9-a28d803ce992748b/?from=
ab9a5f35-410a-40d3-88a6-d27f37dcd725&interface=teacher&class=48&subject=16 - И.И. Зубарева, М.С. Мильштейн, В.Г. Гамбарин. Математика 5. Диск для учителя. “ИМЦ Арсенал образования”
- http://sravni-flagi.narod.ru/index/0-2
Учебные и методические пособия.
- Зубарева И.И., “Математика, 6 класс” учебник для общеобразовательных учреждений, М., “Мнемозина”, 2012
- Зубарева И.И., “Математика. 5-6 классы”. Методическое пособие для учителя, М., “Мнемозина”, 2011
- В.Г. Гамбарин, И.И. Зубарева, “Сборник задач и упражнений по математике. 6 класс”, М., “Мнемозина”, 2012