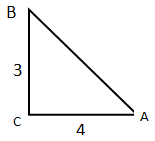Геометрия владеет двумя сокровищами: одно из них – теорема Пифагора…
И. Кеплер
Цели:
- Образовательные: ознакомление учащихся с историей и формулировкой теоремы Пифагора, подведение их к открытию и доказательству её.
- Развивающие: способствовать дальнейшему развитию у учащихся логического мышления, познавательного интереса, формирование первичных умений, связанных с теоремой Пифагора, а также универсальных способов мыслительной деятельности: анализа, обобщения, планирования, конкретизации и рефлексии.
- Воспитательные: воспитывать у учащихся интерес и любовь к предмету.
Оборудование: ПК, мультимедиа-проектор.
Место проведения урока: кабинет математики, оснащенный компьютерами, интерактивной доской.
План урока:
- Приветствие
- Актуализация знаний и фиксация затруднений в деятельности
- Объяснение нового материала
- Закрепление нового материала
ХОД УРОКА
Актуализация знаний
Повторим некоторые геометрические факты
а) Дайте определение прямоугольного
треугольника.
б) Как называются стороны прямоугольного
треугольника.
в) Назовите формулу площади прямоугольного
треугольника.
г) Назовите формулу площади квадрата.
в) Можно ли найти зависимость между сторонами
прямоугольного треугольника?
Существует ли зависимость между катетами и
гипотенузой прямоугольного треугольника?
Да, существует, и она называется теоремой
Пифагора.
Прежде, чем говорить о теореме, выясним кто же
такой Пифагор. К сегодняшнему уроку у вас было
задание, подготовить сообщения из жизни и
деятельности Пифагора. (Слайд 6)
Пифагор родился около 570 г. до н. э. на острове
Самосе. По античным свидетельствам он был красив
и обладал незаурядными способностями.
548 г. до н.э. он прибыл в Навкратис. Научившись
всему, что дали ему жрецы, он отправился на родину
в Элладу.
Во время путешествия был захвачен в плен царем
Вавилона.
В 530 г. до н.э. сбежал из плена на родину. Там
создает «пифагорейскую» школу, в которой
рассматривались четыре науки: арифметика, музыка
(гармония), геометрия и астрономия с астрологией.
Приблизительно в 510 г. до н.э. Покончил жизнь
самоубийством.
А теперь узнаем историю возникновения теоремы Пифагора. (Слайд 7)
Теорема Пифагора – важнейшее утверждение
геометрии. Обычно открытие этого утверждения
приписывают древнегреческому философу и
математику Пифагору. Но изучение вавилонских
таблиц и древних китайских рукописей показало,
что данное утверждение было известно задолго до
Пифагора. Заслуга Пифагора состояла в том, что
он открыл доказательство этой теоремы. (Слайд
8)
В Древнем Китае за 1100 лет до н.э. было установлено
наглядное доказательство теоремы, содержащееся
в древнейшем китайском трактате «Чжоу-би».
За 2000 лет до н.э. древние египтяне знали, что
треугольник со сторонами 3,4,5 есть
прямоугольный (египетский треугольник) и
использовали этот треугольник в «правиле
веревки» для построения прямых углов при
сооружении зданий. (Слайд 9)
Пифагор или кто-то из его учеников нашли формулы
для отыскания бесконечного множества таких
троек: a = 2mn, b = m2 – n2,
c = m2 – n2, где m и
n – любые натуральные числа такие, что m›n.
Кроме этого к нам от Пифагора пришли следующие
термины «квадрат»
для чисел n2, «куб» для чисел n3. (Слайд
10)
Одну из древнейших формулировок и
доказательство данной теоремы изложил Евклид в
своем труде «Начала» придав ей геометрический
характер «Квадрат, построенный на
гипотенузе, равновелик сумме квадратов,
построенный на квадратах» (Слайд 11)
Существует легенда о теореме.
Приведем стихотворение немецкого писателя А. Шамиссо об этом событии.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.Поэтому всегда с тех пор, чуть
Истина рождается на свет быки
Ревут, ее почуя, вслед.Они не в силах свету помешать,
А могут лишь, закрыв Глаза, дрожать
От страха, что вселил в них Пифагор. (Слайд 12)
Существуют различные формулировки теоремы Пифагора.
Например:
«Если дан нам треугольник
И при том с прямым углом,
то квадрат гипотенузы
мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим–
И таким простым путем
К результату мы придем. (Слайд 13)
И наконец, в современной интерпретации теорема звучит следующим образом: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов». (Слайд 14)
Приведем доказательство теоремы.
Доказательство 1
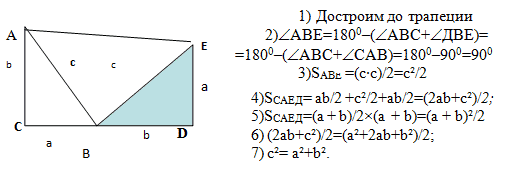
(Слайд 15)
Доказательство 2
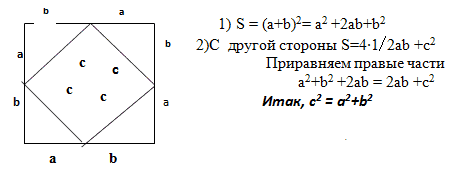
(Слайд 16)
Практическое применение.
С помощью теоремы Пифагора решают разнообразные практические задачи:
– нахождение элементов прямоугольного,
равнобедренного, равностороннего треугольников,
диагоналей квадрата, прямоугольника;
– вычисление расстояния между точками.
Теорема Пифагора позволяет
– устанавливать соотношения между элементами
правильных многоугольников;
–доказывать многие теоремы;
– выводить различные формулы, решать
алгебраические задачи; (Слайд 17)
Практическое задание.
1) Указать треугольники, к которым можно применить т. Пифагора.
(Слайд 18)
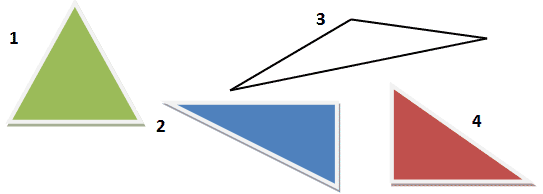
2) Найти неизвестную сторону. (Слайд 20)
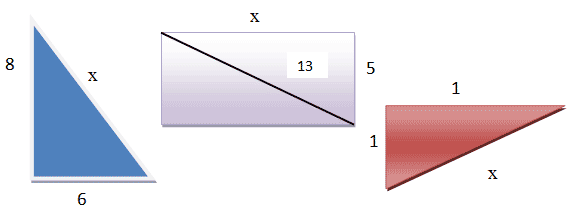
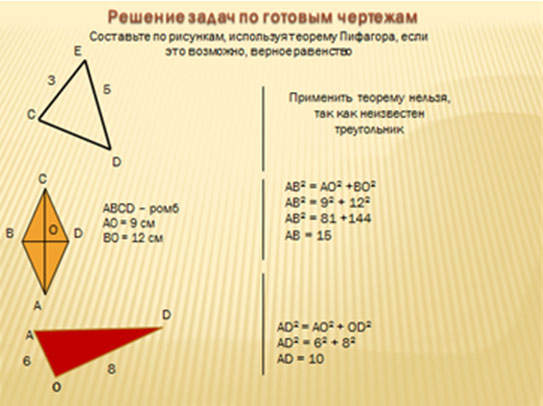
3) Решение задач по готовым чертежам. (Слайд 19)
Проверим ваши знания с помощью теста.
Ответь правильно на вопрос теста, нажав на правильный ответ 1 вопроса и т.д. За каждый правильный ответ теста вы получаете балл. Если вы ответили правильно на все вопросы, то вы получите 5 баллов.
1) Какое из утверждений является теоремой Пифагора.
а) в любом треугольнике квадрат гипотенузы равен сумме квадратов его катетов.
б) в прямоугольном треугольнике квадрат катета равен сумме квадратов другого катета и гипотенузы.
в) в прямоугольном треугольнике гипотенуза равна сумме катетов.
г) в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов. (Слайд 21)
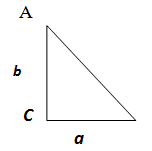
2) Какое равенство выражает теорема Пифагора (а, b, c – сторона прямоугольного треугольника)
а) a2 = b2 + c2;
б) c = a2 + b2;
в) b = a2 + c2;
г) c = a + b; (Слайды 22, 23)
3) Чему равна гипотенуза АВ прямоугольного треугольника АВС ( ‹С = 90о)
а) 7; б) 5; в) 25; г) среди данных ответов правильного нет. (Слайды 24, 25, 26)
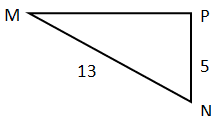
4) Чему равен катет МР прямоугольного треугольника МNP? (P = 90о)
а) 12; б) 8; в) 18; г) среди данных ответов правильного нет.
(Слайды № 27, 28, 29, 30)
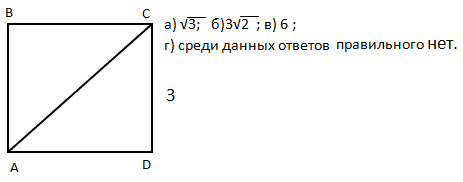
5) Чему равна диагональ квадрата АВСД?
(Слайды 31-35)
– Итак, сегодня мы познакомились с одной из главных теорем геометрии – теоремой Пифагора.
Пребудет вечной истина, как скоро
Все познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век. (Слайд 40)
Домашнее задание. (Слайд 41)
1.Теорема Пифагора. Выучить доказательство.
Подготовить сообщение «Я знаю интересные
сведения из жизни Пифагора».
Найти старинные задачи, связанные с теоремой
Пифагора.
2. № 483, учебник Геометрии 7-9 под редакцией Л.С.
Атанасян, В.Ф. Бутузов и др.
3. № 32.1 задачи по геометрии для 7-11 классов Б. Зив,
В.М. Мейлер.
– Спасибо за урок!