Формирование и диагностика оранизационно-рефлексивных общеучебных умений на уроках математики
У людей, которые усвоили великие принципы
математики, одним органом чувств больше.
(Ч.Дарвин)
На границе тысячелетия время как - будто ускоряет свое движение, возрастает объем информации, увеличиваются возможности и потребности человека. Мир так быстро меняется, что, думается, успеть за ним можно лишь одним способом - опередив его.
Я - учитель математики. Я знаю, что 2х2 будет 4 и сегодня, и завтра, и послезавтра. Но традиционные подходы к изучению математики требуют сегодня изменений. Современные образовательные технологии должны ориентироваться на возможность научить учащихся добывать знания, на развитие способности размышлять, анализировать, формировать самостоятельное и творческое использование полученных знаний - те важные умения, которые в дальнейшем смогут помочь принимать решения и действовать в сложных условиях сегодняшней жизни. Если учитель не заботится постоянно о развитии учащихся, не поставляет им достаточную пищу для ума, то они не смогут состояться как личности. Многовековой опыт человечества доказал, что математика, как наука, имеет для этого богатейшие возможности.
На уроках математики работа с любым учебным заданием требует развития регулятивных умений. Одним из наиболее эффективных учебных заданий на развитие таких умений является текстовая задача, так как работа с ней полностью отражает алгоритм работы по достижению поставленной цели (по П.Я.Гальперину).
Неоценимую помощь в решении этой проблемы оказывают нестандартные задачи. На уроках, развивающих и факультативных занятиях постоянно предлагаю учащимся различные нестандартные задания, требующие мобилизации знаний, умений, напряженной, активной и кропотливой самостоятельной работы.
«Лучшее, что может сделать учитель для ученика, состоит в том, чтобы путем ненавязчивой помощи подсказать ему блестящую идею...», - эти слова Д.Пойя я взяла за девиз успеха в обучении решению нестандартных задам.
В любом деле эффективная реклама играет далеко не последнюю роль. И в математике есть свои «фейерверки»! Почувствовать и оценить красоту математики, силу ее эмоционального воздействия позволяют, в первую очередь, «красивые» задачи. Что же такое красивая задача? Ответ на этот вопрос, естественно, дело вкуса. Вместе с тем опыт показывает, что учащимся нравятся те задачи, решение которых доступно, часто непредсказуемо, по возможности короткое, а самое главное - неожиданное. Опыт показывает, что учащимся нравятся те задачи, решение которых доступно, часто непредсказуемо, по возможности короткое, а самое главное - неожиданное. Умело поставленные учителем наводящие вопросы помогают найти изящное решение задачи, добиться того, чтобы ученик в результате интенсивного творческого труда получил радость от решения трудной для него задачи. Важно помнить, что решение задачи не самоцель, а способ обучения.
Умение решать нестандартные задачи свидетельствуют о глубоком владении математическим аппаратом, а это гораздо важнее, нежели только «чистые» знания, которые нетрудно пополнить с помощью хороших справочников.
Виды универсальных действий
Регулятивные
- «Преднамеренные ошибки»
- Поиск информации в предложенных источниках
- Взаимоконтроль
- Диспут
- «Ищу ошибку»
- Контрольный опрос на определенную проблему
На этапе проверки домашнего задания и актуализации знаний возможно использование компьютера для организации разных видов устного счета, проведения автоматизированных математических диктантов.
Работа по готовому чертежу способствует развитию конструктивных способностей, отработке навыков культуры речи, логике и последовательности рассуждений, учит составлению устных планов решения задач различной сложности.
Целенаправленно учу ребят, что во время решения нестандартных задач часто помогают общие принципы:
- преобразовать задачу к виду, удобному для решения;
- рассмотреть отдельный, простейший случай, а затем обобщить идею решения;
- разбить задачу на несколько простых подзадач;
- обобщить задачу.
В работе рассматриваю некоторые специфические подходы к решению нестандартных задач. Приведу примеры отдельных заданий.
Задача 1. Парус имеет вид четырехугольника АВСД, углы А, С и Д которого равны 45°. Найти площадь паруса, если ВД= 4 м.
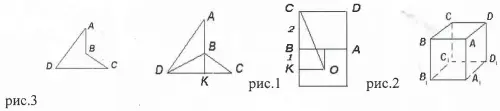
Решение. Пусть прямые АВ и СД пересекаются в точке К (рис.1). В ∆АДК угол А = уголу Д=45°, поэтому СД перпендикулярна АВ, ∆АДК и ∆СВК - прямоугольные и равнобедренные. Пусть АК=ДК= а, ВК= СК= В.
![]()
![]()
Задача 2. АВСД А1В1С1Д1 - куб с ребром 2 см. (рис.3) Паук находится в центре грани АВВ1А1. Какую наименьшую длину может иметь путь паука по поверхности куба в вершину С?
Решение. Совершим «революционный» шаг - изобразим развертку граней А1В1ВА АВСД (рис.2)
![]()
Критерием сформированности регулятивных действий может стать способность:
- выбирать средства для своего поведения;
- планировать, контролировать и выполнять действие по заданному образцу, правилу, с использованием норм;
- планировать результаты своей деятельности и предвосхищать свои ошибки;
- начинать и заканчивать свои действия В нужный момент.
Индивидуальные работы учащихся является одной из ведущих форм компетентностного обучения. Такой активный метод обучения активизирует творческий потенциал учащегося, учит работать с информацией, выбирать главное, систематизировать, анализировать, выбирать наиболее удачный способ представления материала.
В старших классах накопленный опыт позволяет ребятам успешно готовиться и выступать на конференциях исследовательского общества учащихся.
Творческие способности проявляются не в эпизодическом решении отдельных творческих познавательных задач, а при планомерном, целенаправленном предъявлении их в системе. Ну а для того, чтобы УЧИТЬ других, надо прежде всего непрерывно пополнять собственный багаж математических знаний, создавать запас как увиденных, так и собственных методических находок.
Список литературы
- Асмолов А.Г., Бурменская Г.В., Володарская И.А., Карабанова О.А., Салмина Н.Г. Молчанов С.В. Как проектировать универсальные учебные действия: от действия к мысли. - М., 2008.
- Михеева Ю.В. Проектирование урока с позиции формирования универсальных учебных действий. Статья. Учительская газета, 2012.
- Г.Мелхорн Гениями не рождаются. М. Просвещение. 1986.
- А.Г.Мерзляк, М.С.Якир Неожиданный шаг или 113 красивых задач. Киев 1985.