Применение производной к исследованию функции

Предмет

Алгебра и начала математического анализа

Класс

11

Тема

Применение производной к исследованию функции

Тип урока

Урок общеметодологической наполненности (урок обобщения и систематизации знаний)

Время реализации урока

45 минут

Цели урока

Образовательные: создать условия для организации учебной деятельности учащихся по самостоятельному применению комплекса знаний по теме "Применение производной к исследованию функций".
Развивающие: создать условия для развития основ самоконтроля, самооценки, принятия решений и осуществления осознанного выбора через выполнение заданий в конкретной ситуации.
Воспитательные: способствовать формированию ответственного отношения к учению, настойчивости в достижении цели и заинтересованности в конечном результате труда; способствовать воспитанию мировоззрения (патриотическое воспитание) в рамках выполнения задания.

Планируемые результаты

Личностные: включение учащихся в деятельность на личностно-значимом уровне, умение аргументировать, умение контролировать процесс и результат математической деятельности, развитие навыков сотрудничества с учителем и сверстниками в разных учебных ситуациях.
Метапредметные

• Регулятивные: ставить цели деятельности на уроке и сохранять заданную учебную цель, формулировать учебную проблему, определять цель учебной деятельности, выдвигать версии решения проблемы; в диалоге с учителем совершенствовать самостоятельно выработанные критерии оценки.
• Познавательные: совокупность умений сравнивать, классифицировать объекты; совокупность умений по работе с информацией; совокупность умений алгоритмизировать ход решений, умозаключать, делать выводы, использовать знаково-символическоое моделирование.
• Коммуникативные: совокупность умений владения диалоговой речи, умения слушать собеседника, оформлять свои мысли в устной речи, критично относиться к своему мнению и результатам своей деятельности, с достоинством признавать ошибочность своего мнения, если оно таково.

Предметные

• овладение алгоритмами применения производной к исследованию функций (исследование функции на монотонность, исследование функции на экстремумы, исследование функции на наибольшее и наименьшее значения функции на промежутке)

Дидактическая структура урока

1. Организационный этап. Мотивация к учебной деятельности
2. Этап актуализации знаний и фиксации затруднений
3. Этап обобщения и систематизации знаний
4. Самостоятельная работа с самопроверкой, взаимопроверкой
5. Информация о домашнем задании, инструктаж по его выполнению
6. Рефлексия учебной деятельности

Размер мультимедиа компонента

3,42 МБ

Вид мультимедиа компонента

Презентация, разработанная с помощью Microsoft PowerPoint 2013;
«Videouroki.net», «edu.skysmart.ru» - образовательные интернет-ресурс для школьников и учителей

Ресурсы, оборудование, материал

Проектор, компьютер учителя, презентация, проверочная работа в виде теста с «Videouroki.net», задания для домашней работы на сайте «edu.skysmart.ru», 11 компьютеров для учащихся с ОС Windows 7, раздаточный материал.

Список литературы

1. Алгебра и начала математического анализа. 11 класс: учебник для общеобразовательных организаций / [С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин]; М.: Просвещение, 2018. - 464 с.
2. ЕГЭ 2020.Математика. Базовый и профильный уровни. 4000 задач с ответами/ [И.В.Ященко]; М.: 2020. - 704 с.

Ссылки на использованные интернет-ресурсы

http://nasati.ru/konfucij-aforizmy-mudrosti.html
https://videouroki.net/tests/for-class/
https://edu.skysmart.ru/homework/new/519

Используемые педагогические технологии, методы и приемы

Технология учебно-исследовательской деятельности, информационно-коммуникационные технологии, технология проблемного обучения, практико-ориентированный подход
методы: частично-поисковой, проблемный, практический, словесно-наглядный;
приемы: «Верно ли утверждение», «Яркое пятно» (гвоздика);
формы: фронтальная, парная, индивидуальная.

Дополнительная информация.

Урок посвящен 78-летию победы советского народа над фашизмом.

Этап урока

Деятельность учителя

Деятельность учащихся

Формируемые УУД

Организационный момент (мотивационный)
(2 минуты)

Цель: подготовить учащихся к работе на уроке.

Учитель приветствует обучающихся, проверяет их готовность к уроку

На доске: тема урока (слайд 1)
Диалог с обучающимися

- Прокомментируйте высказывание Конфуция, исходя из темы урока.

На доске (слайд 2)
Три пути ведут к знанию:
путь размышления - это путь самый благородный,
путь подражания - это путь самый легкий и
путь опыта - это путь самый горький.

Диалог с учителем

- Понятие производной сложное, находит применение в разных алгоритмах. Когда решаем задачи (путь опыта), можем делать ошибки. Нужно учиться на этих ошибках, чтобы избегать их при выполнении работы.

К: приветствие учителя и одноклассников.
Р: постановка цели урока, оценивать правильность выполнения действия на уровне адекватной оценки.
П: умение владеть математическим языком.
Л: умение слушать и вступать в диалог.

Формулирование цели урока

- Какую цель поставим сегодня на уроке?

Цель: организовать осознание учащимися внутренней потребности к построению учебных действий и фиксированию каждым из них индивидуального затруднения в пробном действии.

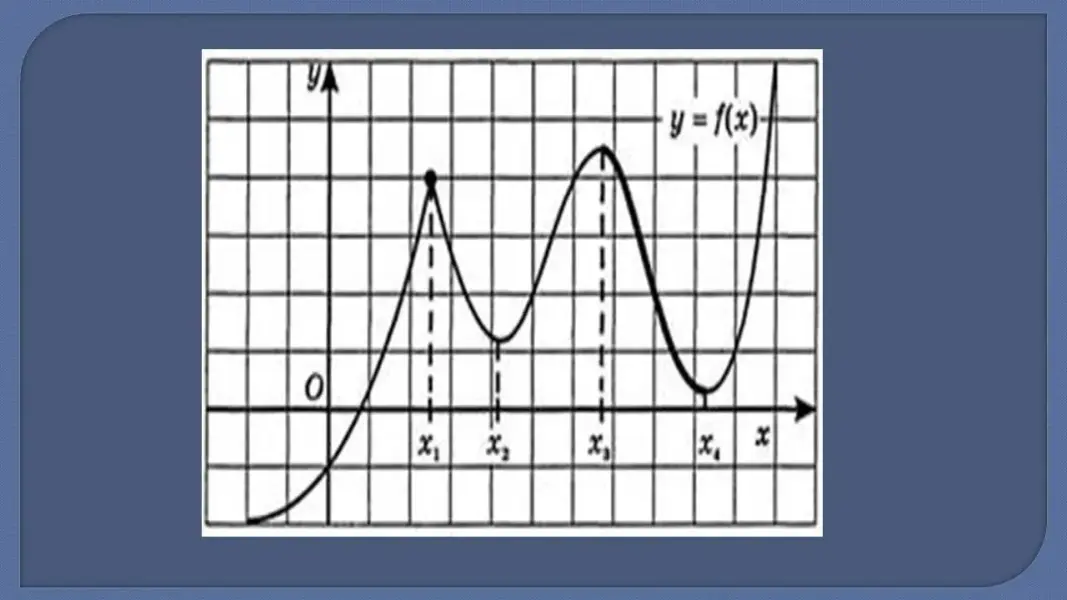
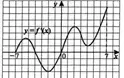
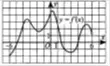
№1. (Задание ЕГЭ по математике). По графику функции ответьте на вопросы:

(слайд 3)

1. Сколько точек максимума имеет эта функция?
2. Назовите точки минимума функции.
3. Сколько промежутков возрастания у этой функции?
4. Найдите длину промежутка убывания.

Л: умение осознавать ответственность за свою страну, понимание ценности человеческой жизни, умение стремиться сочетать личные и общественные интересы, умение к созданию атмосферы подлинного товарищества и дружбы в коллективе
Р: выбор оснований и критериев для аргументации ответа;
анализ с целью выделения существенных признаков; классификация объектов
К: умение обосновывать собственное мнение.

№2. (Задание ЕГЭ по математике). По графику функции ответьте на вопросы:

(слайд 4)

1. Сколько точек максимума имеет эта функция?
2. Назовите точки минимума функции.
3. Сколько промежутков возрастания у этой функции?
4. Назовите наименьший из промежутков убывания этой функции.

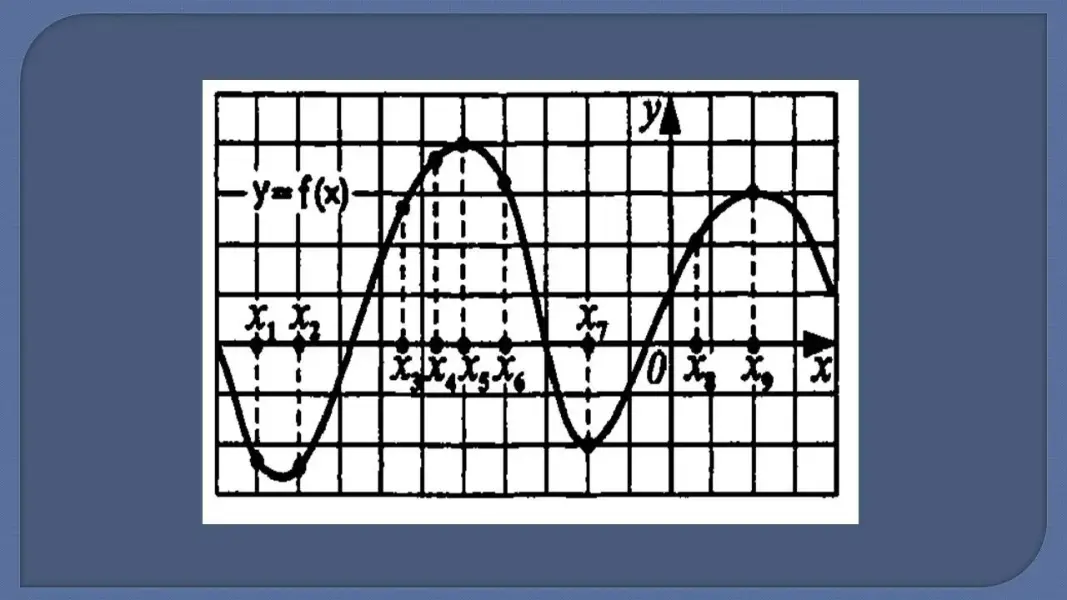
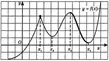
№3. (Задание ЕГЭ по математике). На рисунке изображен график функции и отмечены девять точек на оси абсцисс.

(слайд 5)

Найдите число отмеченных точек, в которых производная отрицательна (положительна).

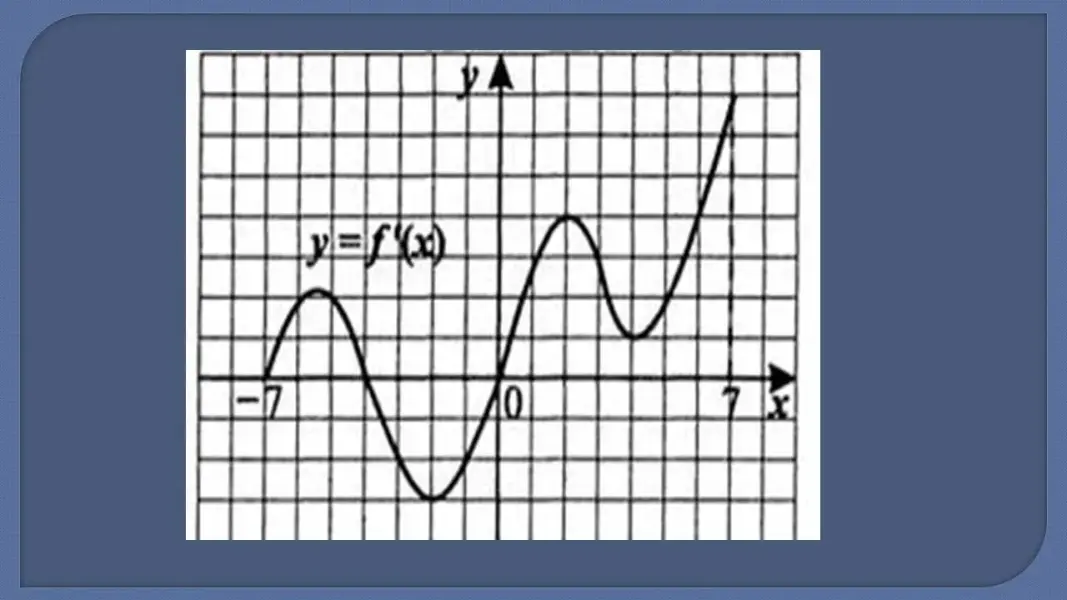
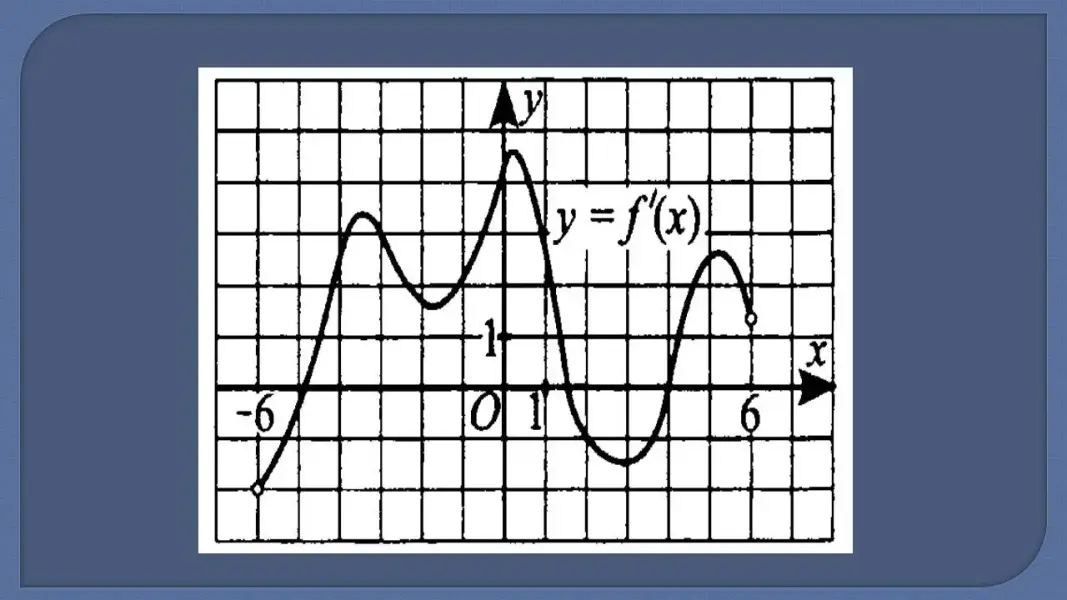
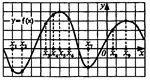
№4. (Задание ЕГЭ по математике). На рисунке изображен график производной непрерывной функции, непрерывной на промежутке.

(слайд 6)

Назовите промежутки убывания функции.
Назовите промежутки возрастания и выберите из них наибольший. Укажите число точек экстремума.

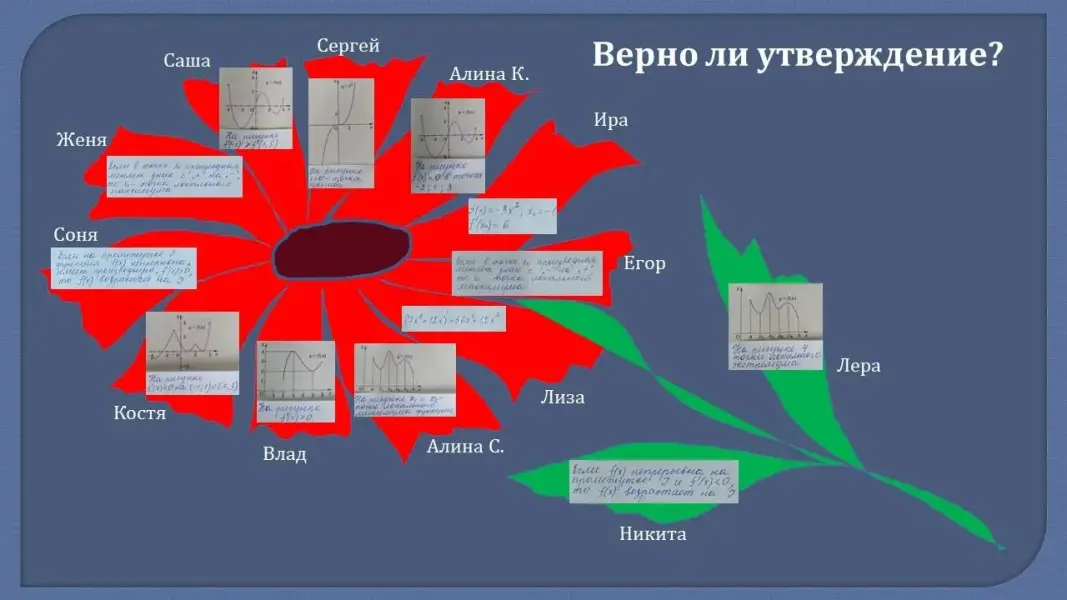
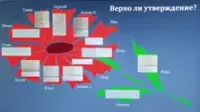
На доске Устное задание: «Верно ли утверждение?» (слайд 7)

- Найдите своё имя, дайте устный ответ на вопрос (да/нет). Обоснуйте свой выбор.

- С каким цветком ассоциируется данный рисунок?
- Символом какого праздника является цветок гвоздика?
Слово учителя:
- Действительно, уже 78 лет мы с гордостью празднуем День Победы советского народа над фашизмом. Благодаря подвигу наших дедов и прадедов, мы живем под мирным небом, учимся, работаем, строим планы. 78 лет мира позволили развить информационные технологии и сегодня мы посвящаем наш урок ветеранам Великой Отечественной войны, Труженикам тыла, всем тем, кто внес свой вклад на пути к Победе над фашизмом.

Обобщение и систематизация материала.
(7 минут)
Цель: закрепить материал по исследованию функции с помощью производной посредством разбора занятия

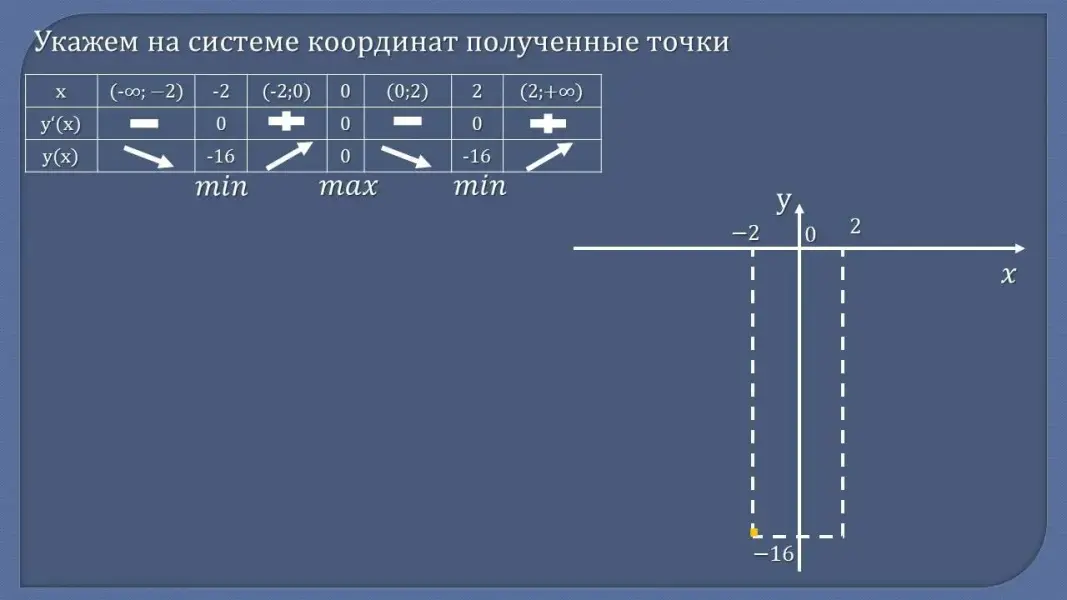
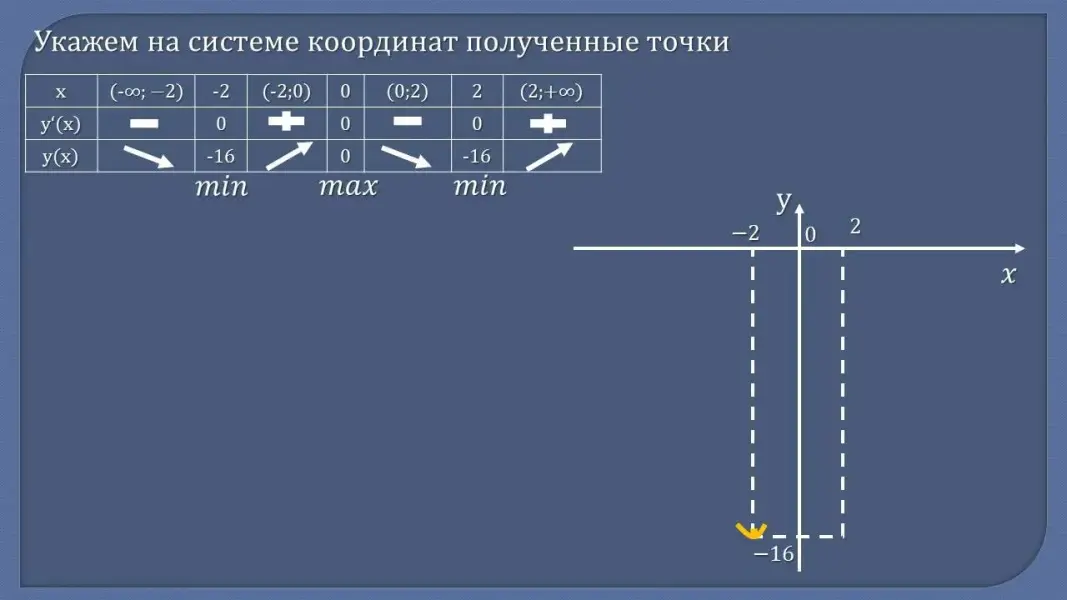
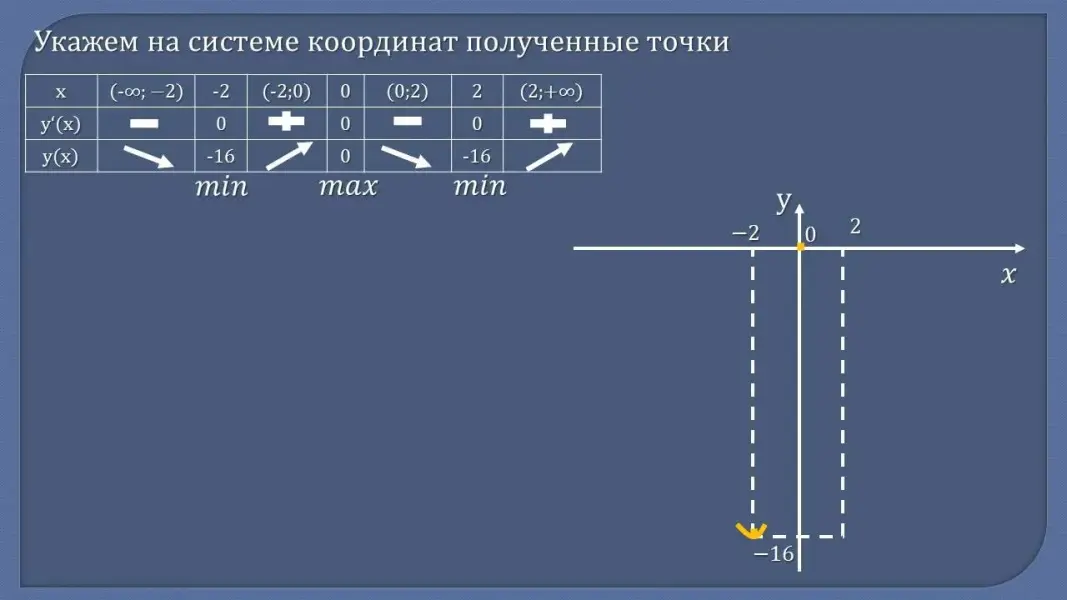
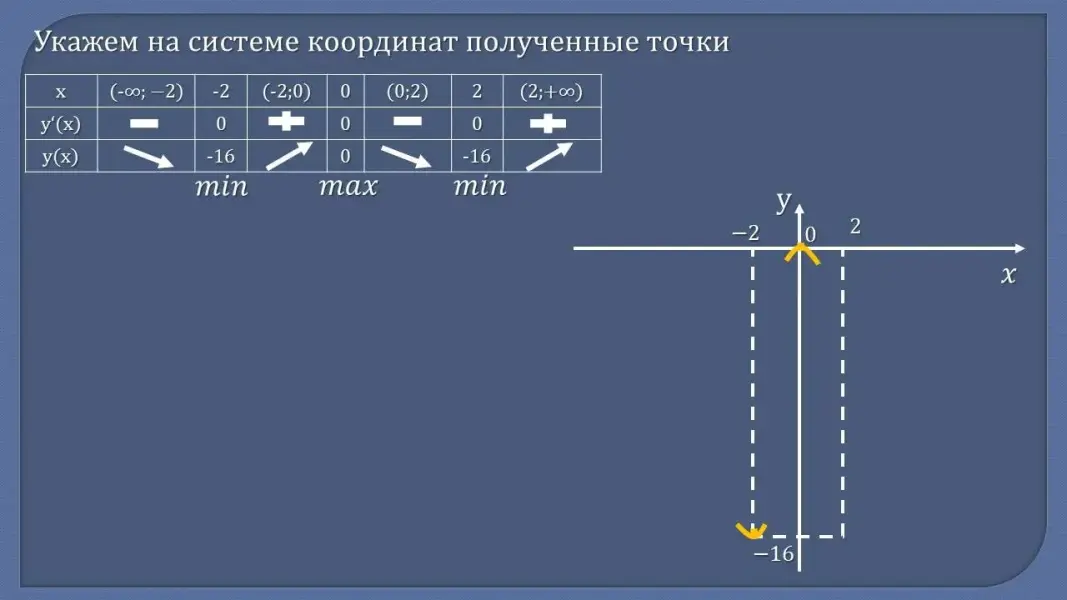
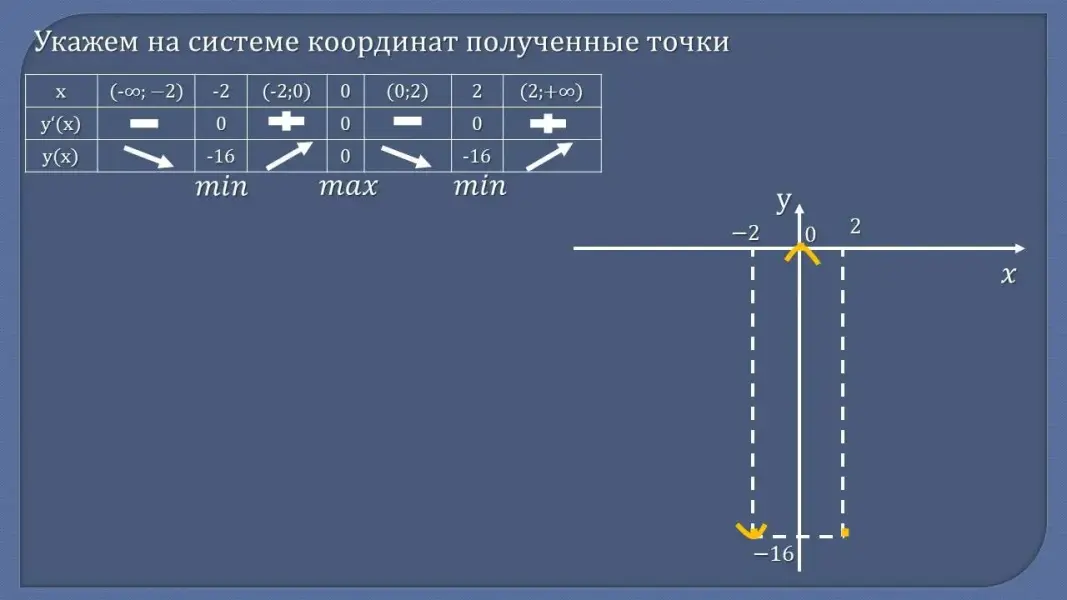
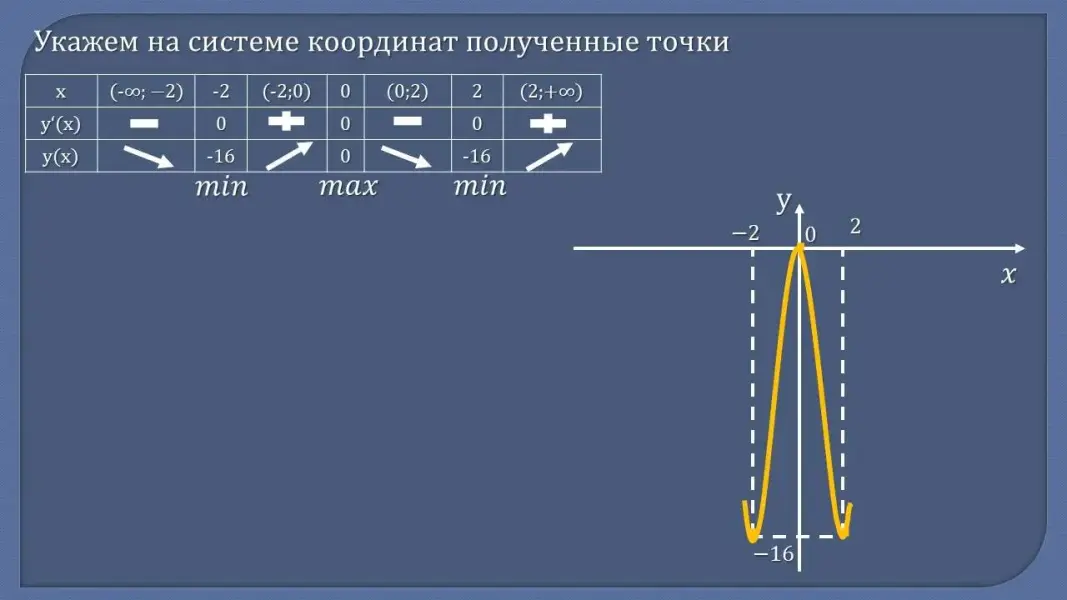
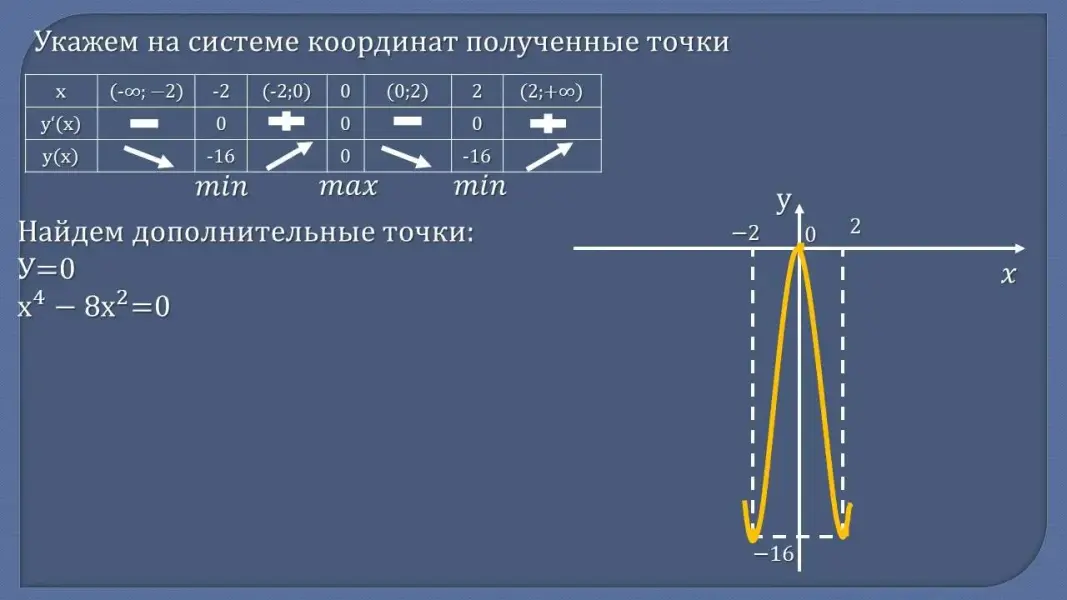
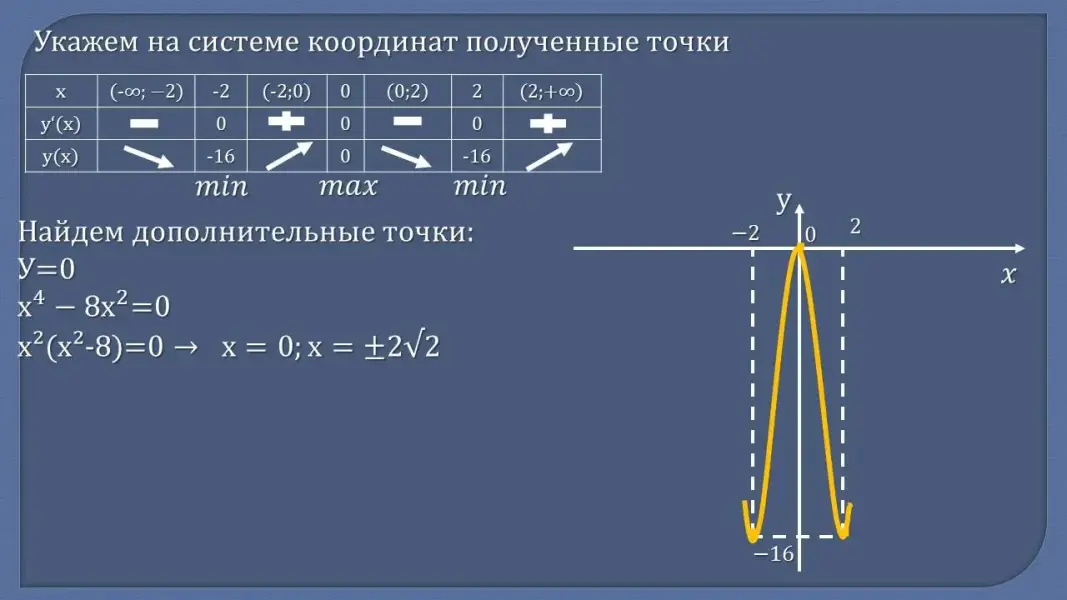
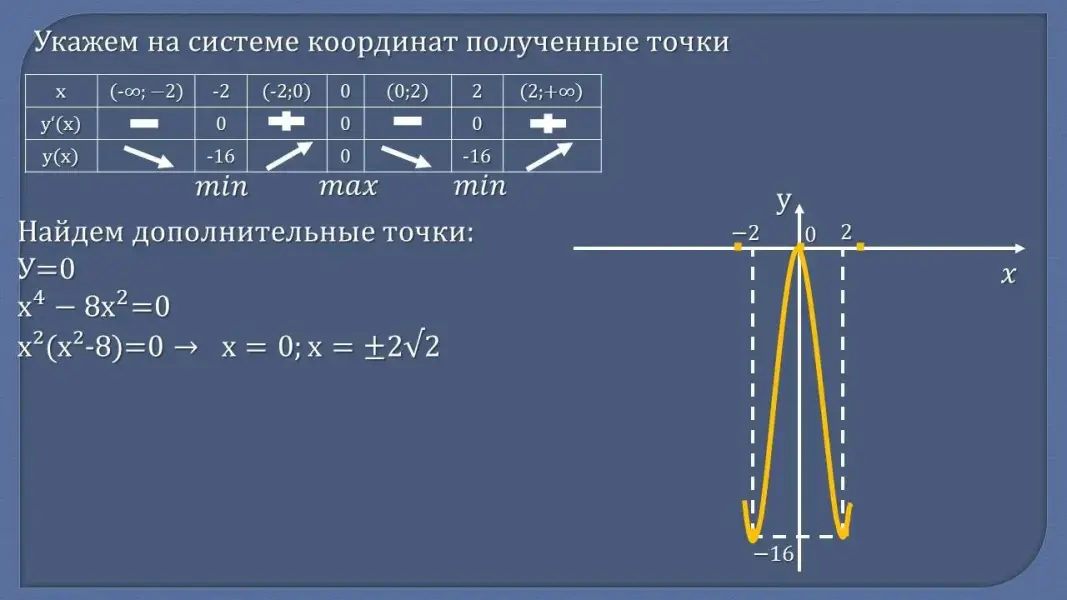
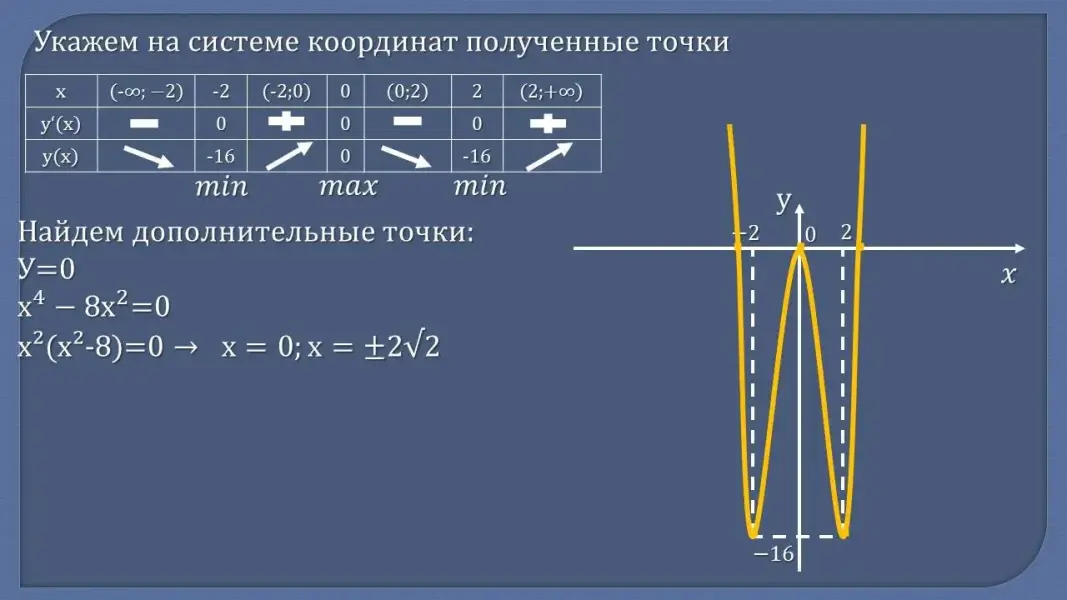
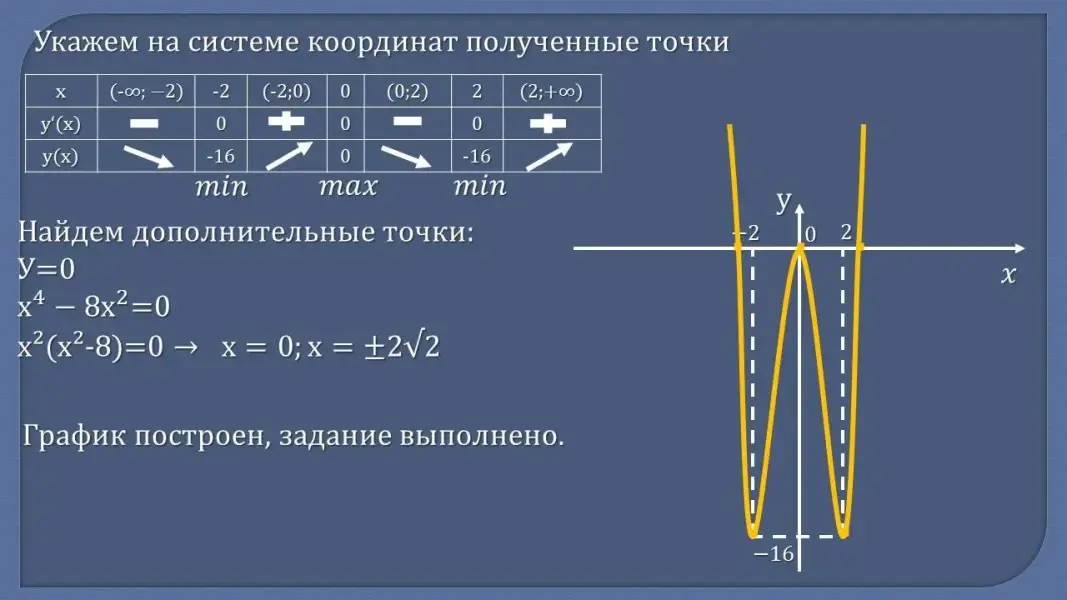
- Сформулируйте алгоритм построения графика функции с помощью производной

- Проверьте себя:
На доске: Алгоритм исследования и построения графика функции с помощью производной (слайд 8)

Рассмотрим функцию у = x⁴ - 8x². По заданному алгоритму исследуем функцию и построим ее график. (Разбор задания)
(слайды 9-55)

Формулируют алгоритм построения графика функции с помощью производной

Выполняют разбор готового решения, задают вопросы учителю

Р: умение определять последовательность действий при исследовании функции; умение сравнивать, анализировать, делать выводы.
П: умение выражать свои мысли в соответствии с поставленной задачей
К: умение строит речевое высказывание

Цель: проверить степень усвоения материала

- Выполните следующее задание аналогично:
Исследовать функцию и построить график: (слайд 56)

1 вариант: у= х³- 3х²+4
2 вариант: у = х³ - 3х + 3

Р: контроль в форме сличения способа действия и его результата с заданным эталоном, коррекция; оценивание качества и уровня усвоения.
П: умение структурировать знания, оценивать процесс и результаты деятельности.
К: умение учитывать
Мнения, отличные от своих. Развитие навыков сотрудничества и управления эмоциями.

- Войдите в личный кабинет образовательного сайта «Videouroki.net», введя логин (код ученика) и пароль одного ученика из пары и выполните 10-минутный тест по теме «Применение производной для отыскания точек экстремума»
(слайд 57)
Приложение 1
(Обучающиеся зарегистрированы на данном сайте с 10 класса, имеют опыт работы с данным интернет-ресурсом)

Проверьте себя, оцените свою деятельность.

Выполняют проверочную работу в парах в онлайн-режиме в форме тестов по теме «Применение производной для отыскания точек экстремума на образовательном интернет-ресурсе для школьников и учителей «Videouroki.net»

Информация о домашнем задании, инструктаж по его выполнению
(1 минута)

Цель: сообщить учащимся о домашнем задании, разъяснить методику его выполнения.

1) Выполните задание к следующему уроку на сайте «edu.skysmart.ru» по теме «Производная и график» (5 упражнений из сборника заданий ЕГЭ по математике, профильный уровень)
(обучающиеся зарегистрированы на данном сайте с 10 класса, имеют опыт работы с данным интернет-ресурсом)
https://edu.skysmart.ru/homework/new/519
Приложение 2

2) Творческое дифференцированное задание в рамках школьной недели математики для желающих (период выполнения - 1 неделя):
- Для учащихся гуманитарного профиля: стихотворение о Великой отечественной войне. Стихотворение оформить для участия в конкурсе стихов о войне, представить на выставку.
- Для учащихся технологического профиля: исследовать функции и построить в одной системе координат графики функций:

Раскрасить плоскость, ограниченную линиями, в цвет георгиевской ленты. Работу оформить для выставки.

3) Нестандартное задание (для профильного уровня):
отыскать функции, описывающие реальные физические процессы, которые вы изучали на уроках физики, и исследуйте их.

Учащиеся задают вопросы по выполнению домашнего задания.

П: умение структурировать знания; оценивание процессов и результатов деятельности.
Р: волевая саморегуляция; осознание того, что уже усвоено и что ещё подлежит усвоению

Этап рефлексии
(2 минуты)

Цель: оценить учащимися свою деятельность и деятельность своих товарищей на уроке

Л: способность к самооценке собственной деятельности
Р: Оценка, выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня подготовки

- Куда мы можем направить наше усердие и волю, пока учимся в школе?

Оцените свою работу на уроке, используя раздаточный материал:
Поставьте знак «+», если с данным видом задания вы легко справляетесь;
Поставьте знак «-», если данный вид задания вызывает трудности

Я хочу вам пожелать, чтобы у вас была только положительная производная, чтобы знания ваши только возрастали, а усердие и воля способствовали этому. Спасибо за урок.

- На учебу.

Учащиеся заполняют таблицу по оценке степени усвоения материала.