Как повысить вычислительную культуру студентов колледжа?

Одним из важнейших способов воспитания трудолюбия, желания и умения хорошо учиться является создание условий, обеспечивающих обучающемуся успех в учебной работе, ощущение радости на пути продвижения от незнания к знанию, от неумения к умению.

Как создать условия для обеспечения этого интереса, интереса к изучению математики? Как показывает педагогический опыт, есть пути, позволяющие вызвать живой интерес к изучению математики у обучающихся любого возраста, различных способностей, склонностей и черт характера. Этот путь лежит через формирование у них вычислительной культуры. Высокая вычислительная культура способствует развитию логического мышления, снятию психологических нагрузок в учении, а значит, и сохранности здоровья у обучающихся, способствует предупреждению отставания в изучении не только математики, но и других учебных дисциплин.

На занятиях по математике приходится сталкиваться с очень низкой вычислительной культурой студентов, а порой и полным ее отсутствием. Неумение считать является таким же невежеством, как для русского человека - неумение грамотно говорить по-русски.

Согласимся с тем, что основы вычислительной культуры должны закладываться в начальных и средних классах школы, но как показывает практика, в колледже студент порой учится считать заново.

Что же включает в себя понятие «вычислительная культура»? Наиболее четкое определение этого понятия дается ведущим научным сотрудником НИИ общего образования РГПУ им. А.И.Герцена, кандидатом педагогических наук, доцентом, Ивашовой Ольгой Александровной. «Вычислительная культура школьников - это учебная вычислительная деятельность, ориентированная на развитие личности ученика в процессе осмысленного овладения ее содержанием (знаниями и умениями математического и общекультурного характера), организованная с учетом социальных условий и характеристик необходимой обществу культуры».

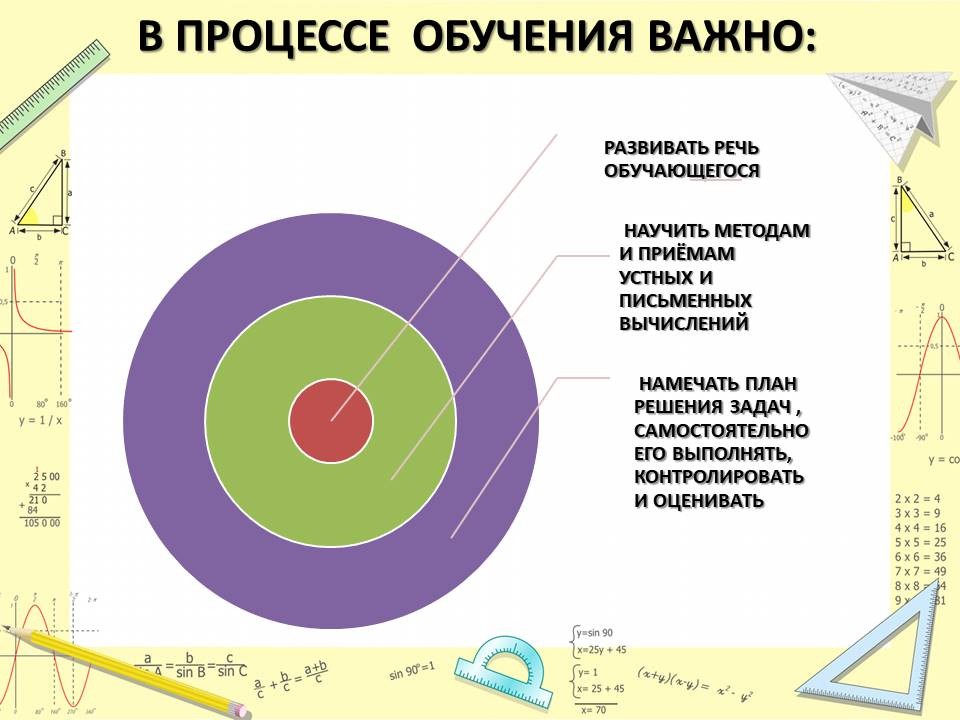
Формирование вычислительной культуры студента влияет на повышение его общей культуры. Поэтому очень важно в процессе обучения развивать речь обучающегося, научить методам и приемам устных и письменных вычислений, намечать план решения задач и самостоятельно выполнять этот план, контролируя и оценивая свою деятельность. Но решение данных задач возможно лишь в специальных условиях, способствующих развитию мышления обучающихся в процессе обучения математике и формированию их вычислительной культуры.

Математика является одной из важнейших наук на земле и именно с ней человек встречается каждый день. Счет в уме является самым древним и простым способом вычисления. Знание упрощенных приемов устных вычислений остается необходимым даже при полной механизации всех наиболее трудоемких вычислительных процессов. Устные вычисления развивают в человеке память, культуру мысли, ее четкость, ясность и быстроту, сообразительность, умение отыскивать наиболее рациональные пути для решения поставленной цели, ясное понимание связи теории с практикой, уверенность в своих силах, помогают обучающимся полноценно усваивать предметы физико-математического цикла.

Вычислительные навыки необходимы как в практической жизни каждого человека, так и в учении. Ни один пример, ни одну задачу по математике, физике, химии и т. д. нельзя решить, не обладая элементарными способами вычислений. В настоящее время во всех областях жизни огромное значение имеют письменные вычисления, но в то же время повседневная практика в магазине, в банке, на производстве, в сельском хозяйстве, а также военное дело требуют умения производить необходимый расчет быстро, точно, подчас на ходу.

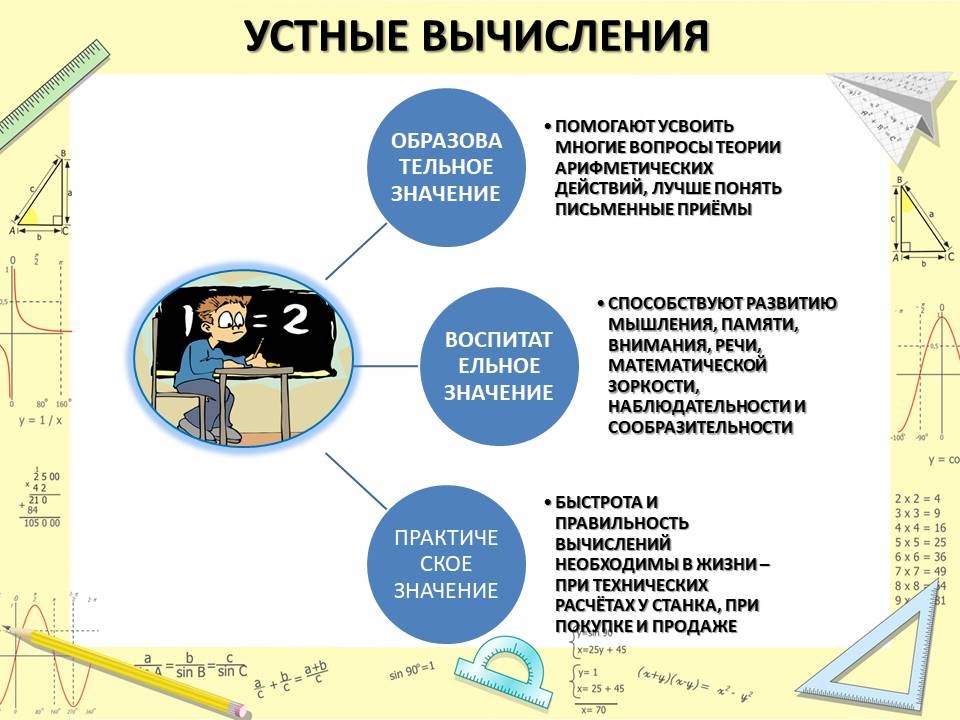
Устный счёт — математические вычисления, осуществляемые человеком без помощи дополнительных устройств (компьютер, калькулятор, и т. п.) и приспособлений (ручка, карандаш, бумага и т.п.). Устные вычисления имеют большое образовательное, воспитательное и практическое и чисто методическое значение:

- образовательное значение: устные вычисления помогают усвоить многие вопросы теории арифметических действий, а также лучше понять письменные приемы;

- воспитательное значение: устные вычисления способствуют развитию мышления, памяти, внимания, речи, математической зоркости, наблюдательности и сообразительности;

- практическое значение: быстрота и правильность вычислений необходимы в жизни, особенно когда письменно выполнить действия не представляется возможным (например, при технических расчетах у станка, в поле, при покупке и продаже).

Из всего вышесказанного следует актуальность задачи разработки стратегии применения разного вида упражнений устного счета для лучшего усвоения нового материала и закреплении пройденного.

Чтобы навыки устных вычислений постоянно совершенствовались, необходимо установить правильное соотношение в применении устных и письменных приёмов вычислений, а именно: вычислять письменно только тогда, когда устно вычислять трудно.

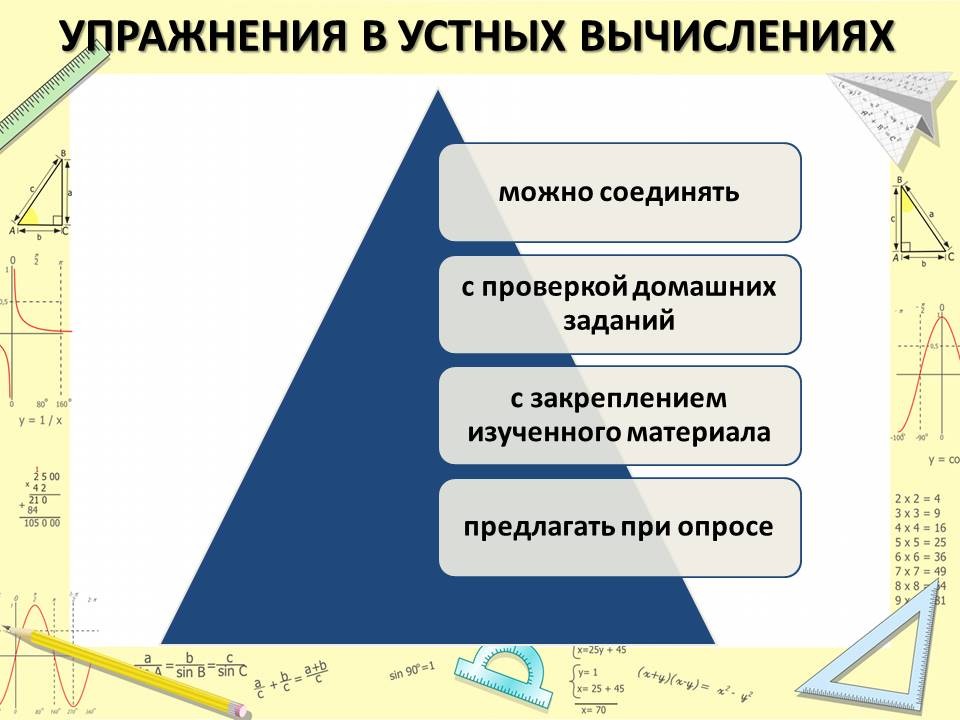
Упражнения в устных вычислениях должны пронизывать все занятие. Их можно соединять с проверкой домашних заданий, закреплением изученного материала, предлагать при опросе. Особенно хорошо, если наряду с этим, специально отводить 5-7 минут на занятии для устной работы. Материал для этого можно подобрать из учебника или специальных сборников. Устные упражнения должны соответствовать теме и цели занятия и помогать усвоению изучаемого на данном занятии или ранее пройденного материала. В зависимости от этого преподаватель определяет место устной работы на занятии. Если устные упражнения предназначаются для повторения материала, формирования вычислительных навыков и готовят к изучению нового материала, то лучше их провести в начале занятия до изучения нового материала. Если устные упражнения имеют цель закрепить изученное на данном занятии, то надо провести устную работу после изучения нового материала. Не следует проводить её в конце занятия, так как ребята уже утомлены, а устная работа требует большого внимания, памяти. Количество упражнений должно быть таким, чтобы их выполнение не переутомляло обучающихся и не превышало отведенного на это времени занятия.

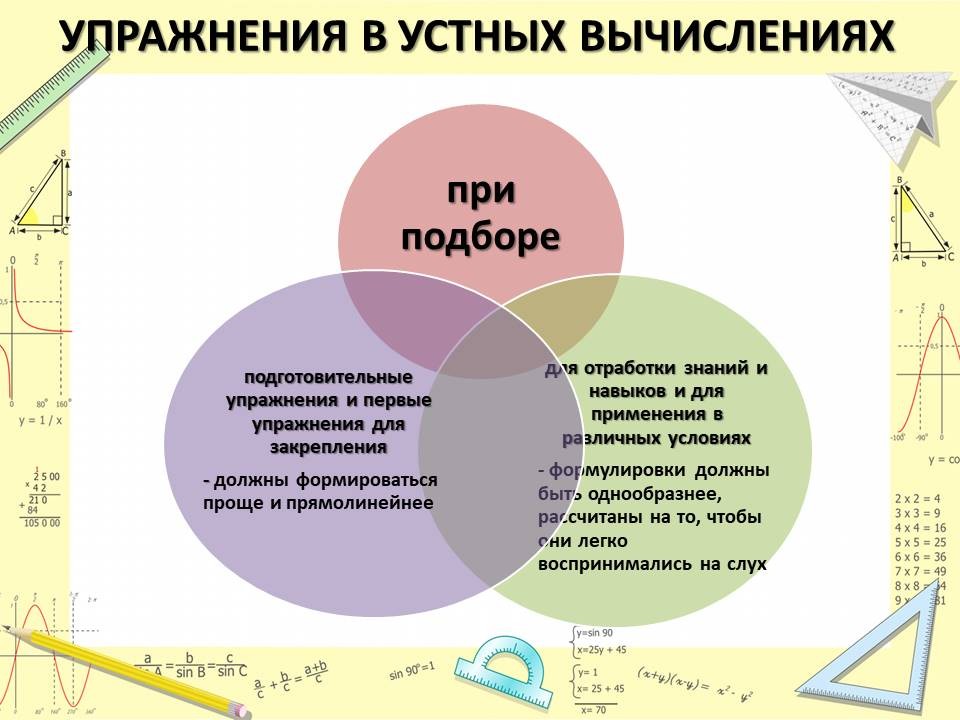
При подборе упражнений для занятия следует учитывать, что подготовительные упражнения и первые упражнения для закрепления, как правило, должны формироваться проще и прямолинейнее. Здесь не нужно стремиться к особенному разнообразию в формулировках и приёмах работы. Упражнения для отработки знаний и навыков и особенно для применения их в различных условиях, наоборот должны быть однообразнее. Формулировки заданий, по возможности, должны быть рассчитаны на то, чтобы они легко воспринимались на слух. Для этого они должны быть чёткими и лаконичными, сформулированы легко и определённо, не допускать различного толкования. В случаях, когда задания всё-таки трудны для усвоения на слух, необходимо прибегать к записям или рисункам на доске.

Помимо того, что устная работа на занятиях математики способствует развитию и формированию прочных вычислительных навыков и умений, она также играет немаловажную роль в привитии и повышении у обучающихся познавательного интереса к занятиям математики, как одного из важнейших мотивов учебно-познавательной деятельности, развития логического мышления и развития личностных качеств обучающегося. На наш взгляд, вызывая интерес и прививая любовь к математике с помощью различных видов устных упражнений, преподаватель будет помогать студентам активно действовать с учебным материалом, пробуждать у них стремление совершенствовать способы вычислений и решения задач, менее рациональные заменять более совершенными. А это - важнейшее условие сознательного усвоения материала.

Устные упражнения позволяют обеспечить нужное количество повторений на разнообразном материале, постоянно поддерживая и сохраняя положительное отношение к математическому заданию.

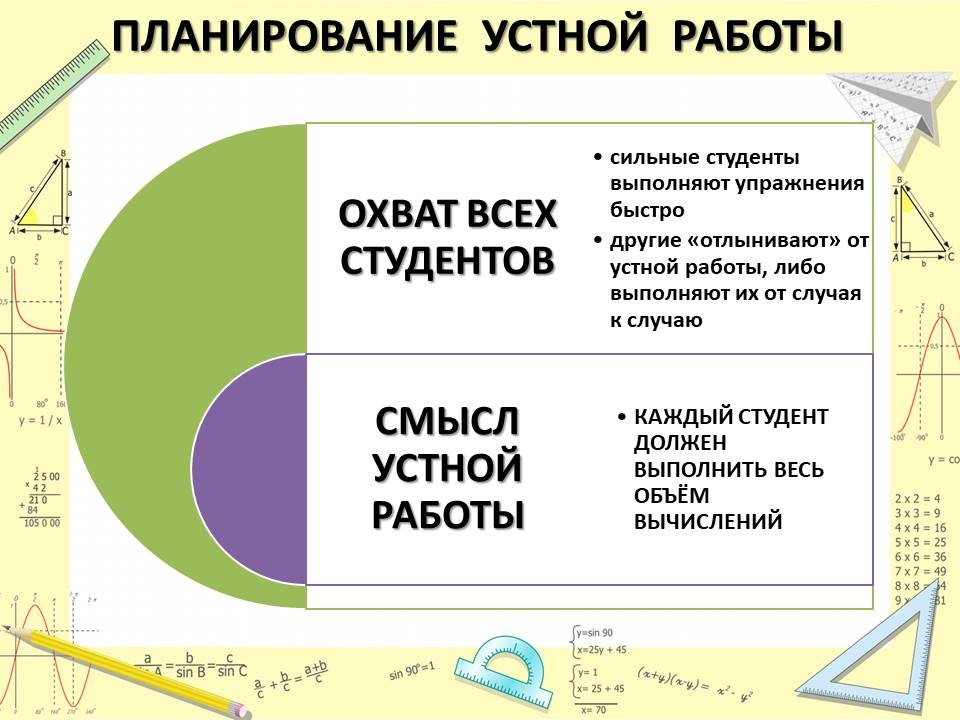
Все сталкиваются при устной работе с такой проблемой, как охват всех студентов. При наполняемости групп в среднем по 30 человек, это довольно проблематично. Как правило, группы по силам неоднородны, сильные студенты выполняют все упражнения довольно быстро, это приводит к тому, что либо постоянно отвечают одни и те же, либо им становится скучно. Другие же имеют возможность либо вообще «отлынивать» от устных упражнений, либо выполнять их от случая к случаю. Смысл же заданий устной работы в том, чтобы каждый студент выполнил весь объем вычислений, а преподаватель имел возможность быстро и легко проверить работу обучающихся.

Поэтому при планировании устной работы в начале урока можно поступить следующим образом: на доску выписываются номера заданий из учебника, предназначенные для устной работы. Студентам дается определенное количество времени, в зависимости от количества заданий. Все вычисления и рассуждения студенты производят устно, записывая только конечные результаты, причем именно в той последовательности, в какой были предложены задания. Через отведенное время задания проверяются. Одновременно преподаватель берет на проверку 4–5 тетрадей с последующим выставлением оценок.

Можем предложить для устной работы и такую форму, она применима в тех ситуациях, когда требуется «набить» руку на использовании определенных алгоритмов.

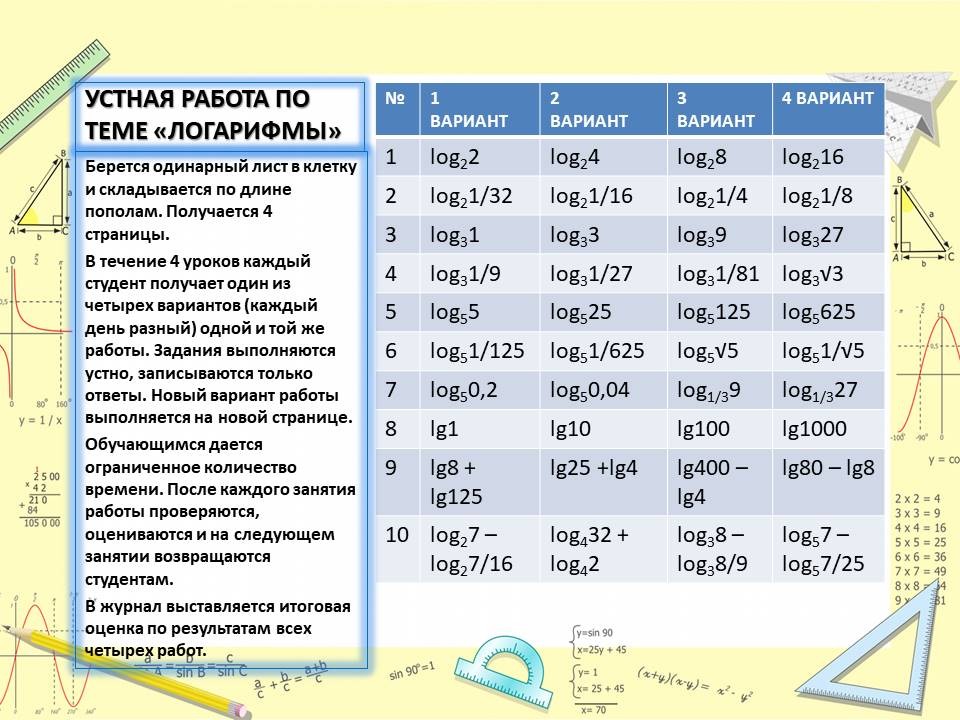
Берется одинарный лист в клетку и складывается по длине пополам. Получается 4 страницы.

В течение 4 уроков каждый студент получает один из четырех вариантов (каждый день разный) одной и той же работы. Задания выполняются устно, записываются только ответы. Новый вариант работы выполняется на новой странице. Обычно берется 10 заданий в каждом варианте, которые охватывают все возможные случаи данной темы. Обучающимся дается ограниченное количество времени. После каждого занятия работы проверяются, оцениваются и на следующем занятии возвращаются студентам.

В журнал выставляется итоговая оценка по результатам всех четырех работ. Такой вид работы позволяет к четвертому занятию существенно улучшить качество и увеличить процент выполнения работ.

Устная работа по теме «Логарифмы»

Устная работа на уроках математики весьма оживляет урок. На ней можно отдохнуть; в хорошем смысле этого слова, развлечься. Это самый «свободный» этап урока. Вопросы быстро сменяют друг друга, и если не знаешь ответ на один, то не беда, сможешь проявить себя на следующем. Это очень динамичный, активный вид деятельности, вносящий разнообразие в занятия математики. Кроме того, каждый студент может отличиться «заработать» поощрение, высокий балл и т.п.

Устные упражнения активизируют мыслительную деятельность обучающихся, развивают внимание, наблюдательность, память, речь, быстроту реакции, повышают интерес к изучаемому материалу. Они дают возможность изучить большой по объему материал за более короткий промежуток времени, позволяют преподавателю судить о готовности группы к изучению нового материала, о степени его усвоения, помогают выявлять ошибки студентов.

Но далеко не всегда устные упражнения приводят к ожидаемым результатам. Причина этого в том, что методика проведения устных упражнений сложнее, чем письменных. Когда группа записывает решение задания, преподаватель видит, кто работает и как работает, видит в тетрадях также и результаты работы. А как проверить, действительно ли все студенты активно думают над заданием при ее устном решении? Отвечает-то всегда чаще всего один студент и сообщает он, как правило, только результат выполненного упражнения, а процесс его получения остается скрытым.

Основные дидактические функции такого момента занятия как устная работа дают ему, по нашему мнению, существенные преимущества, позволяющие его считать неотъемлемой частью каждого практического занятия:

- актуализация опорных знаний студентов и их подготовка к восприятию нового материала;

- более сознательное, неформальное усвоение материала учебного занятия;

- систематическое повторение изученного;

- развитие у студентов внимания, памяти, наблюдательности, сообразительности, инициативы и т.п.;

- формирование интереса к предмету;

- активизация учебной деятельности на занятии.

Проводя устные упражнения, преподаватель должен быть уверен, что работают все, и притом активно. Он должен также получить обратную информацию: как выполнили упражнение, усвоен ли способ решения. Отсюда вывод: чтобы гарантировать участие в работе всех студентов, нужно, очевидно, соблюдать ряд условий эффективности устных упражнений. Рассмотрим их.

1. Желательно, чтобы задачи для устных упражнений были заранее выписаны на отдельных листах или на доске, чтобы каждый студент на протяжении всего процесса устного решения видел эти задания.

2. Условия геометрических задач, решаемых устно, желательно задавать хотя бы частично на чертеже.

3. Устные упражнения желательно чередовать с письменным выполнением упражнений аналогичного типа на самостоятельных и контрольных работах. Если это условие нарушается, то оказывается, что через какое-то время многие студенты не могут справиться на контрольной работе с такими же задачами, которые они решали устно.

4. Во время устных упражнений следует особенно тщательно соблюдать паузы, чтобы обучающиеся успевали обдумать решения задач.

5. При устном решении задач особенно важно соблюдать принципы построения системы упражнений (однотипности, непрерывного повторения, использования контрпримеров и т.д.).

Большое значение на каждом уроке имеет его организационный момент. Как быстро настроить студентов на работу, но сделать это без понуканий и строгости? Можно провести оргмомент в виде математической зарядки.

Заранее готовится несколько слайдов с простейшими примерами. Примеры даются с ответами. На одних слайдах ответы верные, на других – неверные. Каждое упражнение зарядки состоит их двух движений. Преподаватель поочередно показывает группе слайд, а студенты делают определенное движение. Например, если верный ответ – поднимают руку вверх, неверный – вытягивают руку вперед. Сначала студенты не могут собраться, не попадают в ритм. Но постепенно сосредотачиваются, а темп зарядки увеличивается. И в результате мы получаем аудиторию, полностью подготовленную к работе.

Комплекс математической зарядки по теме «Производная» предлагается ниже.

Желательно сделать так, чтобы устная работа воспринималась обучающимися как интересная игра. Тогда они сами следят за ответами друг друга.

Опишем некоторые формы проведения устной работы. Для этого эффективно использование мультимедийной презентации.

Беглый счет. Преподаватель показывает слайд с заданием и тут же громко прочитывает его. Студенты устно выполняют действия и сообщают свои ответы. Слайды быстро сменяют один другой, но последние задания предлагаются уже не с помощью слайда, а только устно.

Для таких упражнений полезно подобрать такие, в которых особенно заметен эффект прикидки.

Пример:

Равный счет. Преподаватель записывает на доске упражнения с ответом. Студенты должны придумать свои примеры с тем же ответом. Их примеры на доске не записываются. Ребята должны на слух определять, верно ли составлен пример, на слух воспринимать названные числа. Пример: p₂ = 0,2

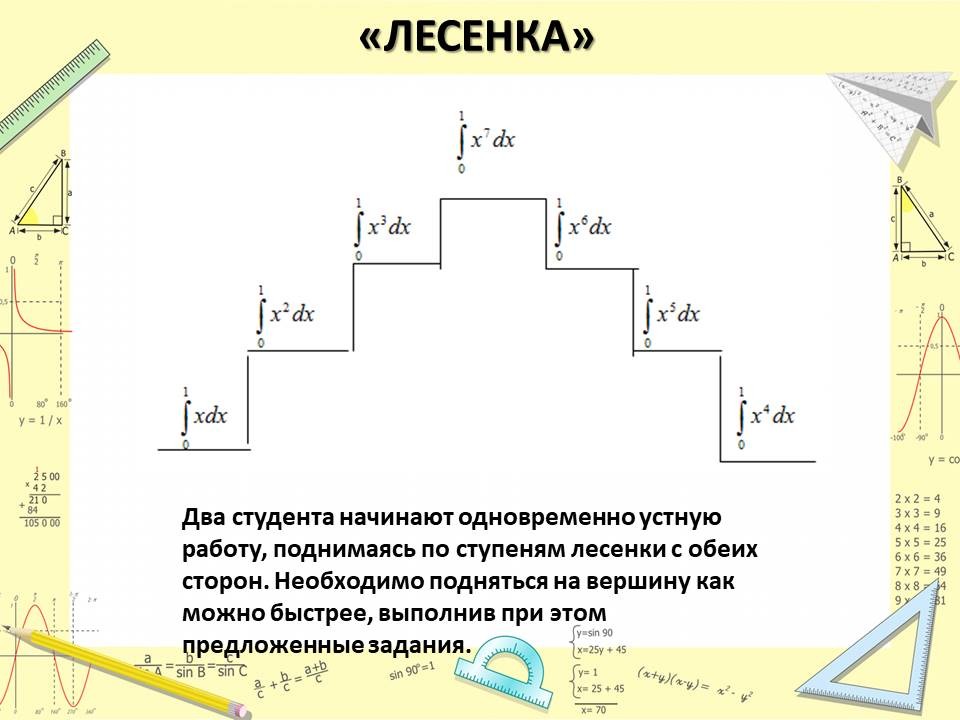
Рис. к «Лесенке»

«Торопись, да не ошибись». Эта игра – фактически математический диктант. Преподаватель медленно прочитывает задание за заданием, а студенты на листочках пишут свои ответы.

Пример:

1) Из 400 зарегистрированных браков 50 распадаются в течение первого года. Найдите относительную частоту расторжения брака в течение первого года.

2) Из 200 изготовленных на заводе пылесосов 4 оказываются бракованными. Какова вероятность того, что при покупке попадется бракованный пылесос?

3) Из 100 дисков 5 оказались непригодными. Какова вероятность того, что наудачу выбранный диск будет пригоден для использования?

4) Монету бросили 2 раза. Какова вероятность того, что оба раза выпадет орел?

5) Монету бросили 2 раза. Найдите вероятность того, что оба раза не выпадет орел?

При изучении курса геометрии большой популярностью пользуются, конечно, упражнения на готовых чертежах. Они позволяют быстро решить большое количество задач, подготавливают студентов к построению более сложных чертежей.

При изучении курса стереометрии визуальные барьеры студентов минимизируются, если личный опыт их обогащён умениями:

• видеть геометрическую конфигурацию в разных ракурсах, зрительно вычленять разные фигуры на одном и том же изображении;
• абстрагироваться от фона на планиметрической или стереометрической конфигурации;
• считывать с рисунка закодированную в обозначениях логическую информацию о свойствах фигур;
• доверять логической информации в обозначениях больше, чем и изображению, воспринимаемому визуально достоверным или недостоверным;
• восстанавливать визуально достоверное изображение, адекватное логической информации в обозначениях, на визуально недостоверном изображении.

Формирование каждого из названных умений требует длительной кропотливой работы. Их стихийное формирование доступно лишь наиболее сильным студентам. Планомерную работу по формированию этого комплекса умений нужно начинать как можно раньше, по крайней мере с первых занятий изучения систематического курса геометрии.

Подводя итоги разговора, приведем еще несколько практических рекомендаций по проведению устной работы на занятии:

• Начинать устную работу следует с более легкого упражнения, постепенно усложняя задания. Это делается, с одной стороны, для того, чтобы студенты постепенно втянулись в относительно быстрый ритм устной работы, а с другой – чтобы не подавить их инициативу и активность.
• Продолжительность не должна превышать 10 минут (оптимально 7-8 минут).
• Планировать устную работу лучше в конце подготовки конспекта, чтобы представлять все занятие в целом, его основные общие и конкретные задачи.
• Устная работа – это прекрасное, активное, мобилизующее, настраивающее на работу начало занятия. Отчасти это связано с тем, что, как известно, в начале занятия (приблизительно на третьей минуте) наступает первый кризис внимания студентов. Второй кризис внимания, как правило, бывает в середине занятия. В это время тоже хорошо отвлечь ребят несколькими уместными устными упражнениями.
• Чтобы стимулировать активность, инициативу студентов, дать возможность проявить себя, можно ввести соответствующую систему оценок во время устной работы (знаковую, балльную и т.д.).
• В устной работе особенно ярко проявляется еще один аспект современного обучения – она дает возможность для формирования и развития диалоговой культуры студентов, которая является элементом общей культуры современного человека. Она дает умение вести диалог с собеседником, т.е. умение общаться, убеждать, слушать его. Это умение необходимо при ведении диалога с компьютером.

Литература

1. Арутюнян Е.Б. Математические диктанты. – М.: Просвещение, 1997.
2. Гончар Д. Р. Устный счёт и память: загадки, приёмы развития, игры // В сб. Устный счёт и память. - Донецк: Сталкер, 1997. 
3. Кононов А.Я. Устные занятия по математике. – М.: Столетие, 1997.
4. Лукин Р.Д., Лукин Т.К., Якунина М.С. Устные упражнения по алгебре и началам анализа. – М.: Просвещение, 1989.
5. Рабинович Е.М. Геометрия. Задачи и упражнения на готовых чертежах. - Харьков: Гимназия, 1991.
6. Устные вычисления и быстрый счет. Тренировочные упражнения за курс 7-11 классов. - Ростов-на-Дону: Легион, 2010.