Задачи на проценты в ГИА

Цели:

• формирование целостного восприятия мира у учащихся;
• развитие научного стиля мышления;
• связать знания с практикой;
• систематизировать знания учащихся, развитие самостоятельности мышления, усиление мотивации обучения, проявление творческих способностей;
• воспитывать аккуратность и точность при подготовке программы, повышать мотивацию учащихся за счет интеграции с другими предметами;
• развитие познавательного интереса, воспитание информационной культуры.

1. Устные упражнения

№1. Найти:

а). 2% от 600; 15% от 45; 6%  от 120.

б). 7%  от 45 руб.; 14% от 2 т; 25% от 16 м; 140% от 250 руб.

№2. Банк предлагает своим клиентам следующие условия вклада: деньги кладутся на счет на 31день, по истечении которых клиент получает доход, равный 7,5 %от вложенной суммы. Какую сумму нужно положить на счет, чтобы доход составил 1500 рублей? (7,5% - 0,075;  1500 : 0,075=20000 руб.)

№3. Рабочий, получив прибавку к своей зарплате 10%, стал получать 32100 рублей. Какую зарплату получал рабочий до прибавки?

№4. 60% некоторого числа равны 180. Чему равны 15% того же числа?

№5. Сберегательная касса выплачивает вкладчику2% годового дохода. Сколько выплатит сберкасса процентных денег вкладчику за 9 месяцев, если вклад составляет 1600 рублей? (32 рубля – за 1 год, 9 месяцев - 3/4 года, за 9 месяцев сберкасса выплатит 32 · 3/4=24 рубля)

2. Проверка домашнего задания

3. Работа по теме урока

Учитель математики: Сегодня у нас не обычный урок. Рассмотрим текстовые задачи на проценты (экономические задачи), которые можно решать не только с конкретными числами, но и в общем виде. Это позволит решать целый класс однотипных задач, отличающихся лишь числовыми данными. А необычность урока заключается в том, что мы составим программы для решения любой задачи данного типа с помощью компьютера.

Рассмотрим задачу №1

Даны два куска с различным содержанием олова. Первый, массой 300 г, содержит 20% олова. Второй, массой 200 г, содержит 40% олова. Сколько процентов олова будет содержать сплав, полученный из этих кусков?

Решение: В задачах такого типа предполагается, что в процессе сплавления нет потерь массы, то есть масса сплава равна сумме масс сплавляемых кусков. (Ученик решает задачу)

1. Переведем 20% и 40% в дроби. 20%=0,2 ; 40%=0,4, тогда в первом куске до сплавления было 3000,2=60(г) олова.

Во втором куске: 200 олова.

В двух кусках было 60+80=140(г) олова.

200+300=500 (г) масса куска после сплавления.

· 100 = 28% олова содержит сплав, полученный из этих кусков.

Ответ: 28%.

Учитель математики: А теперь решим задачу в общем виде и выведем формулу, которая поможет составить программу для решения типовых задач на уроках информатики.

Задача №2

Найдите процентное содержание олова в сплаве, полученном из двух кусков массой m₁ и m₂, если известно, что первый содержит С₁%, а второй – С₂% олова.

Решение:

Обозначим процентное содержание олова в первом куске через С₁, во втором куске через С₂ и в сплаве через С. Масса первого куска m₁(г), масса второго куска m₂(г). Найти процентное содержание олова в сплаве, то есть С(%).

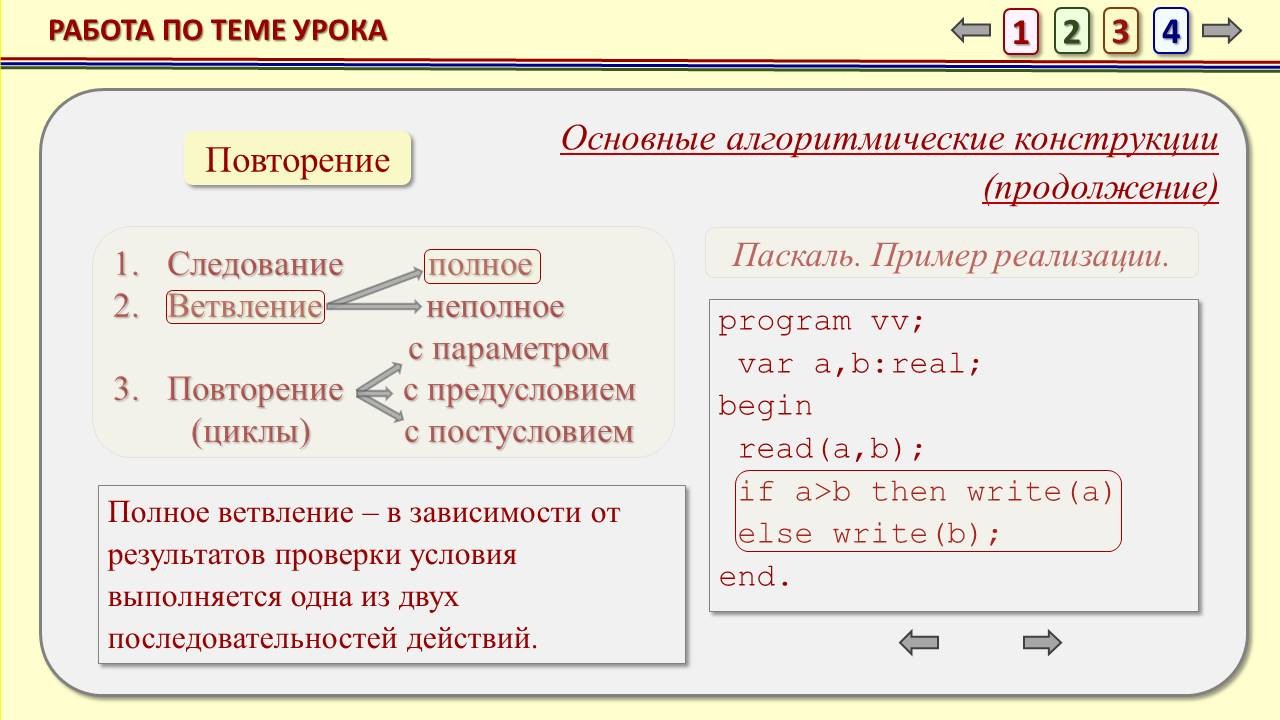
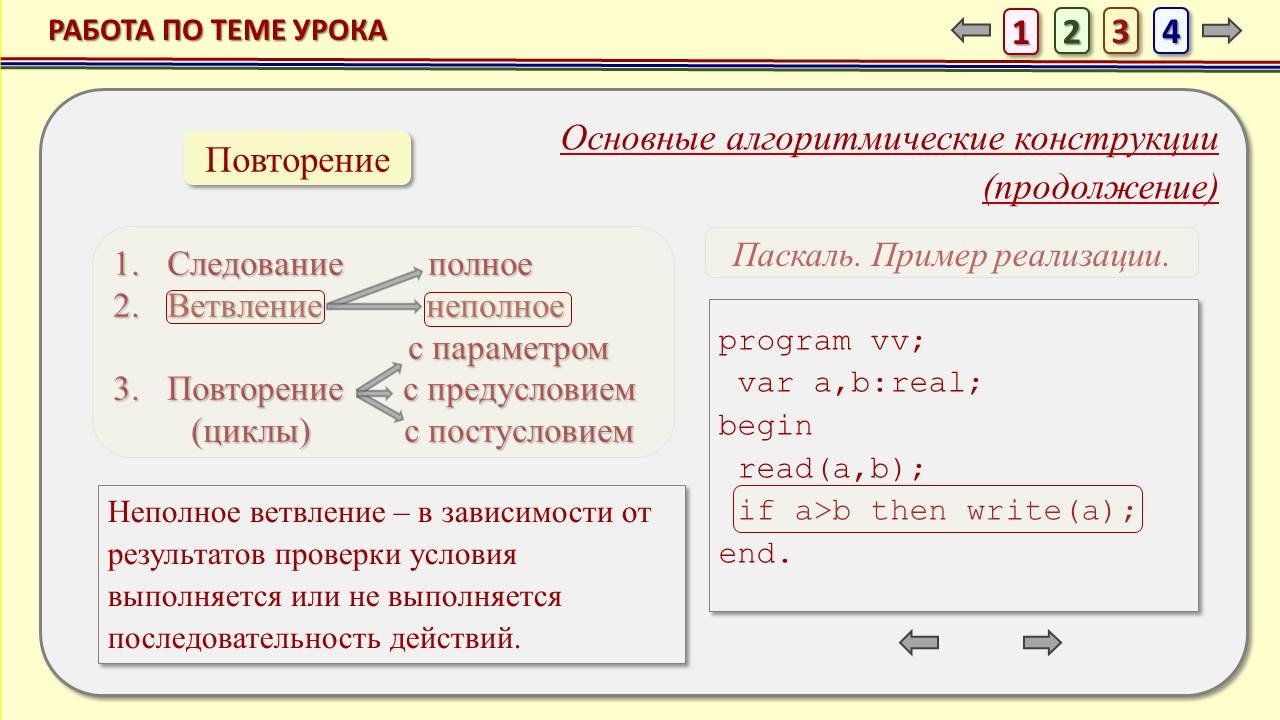
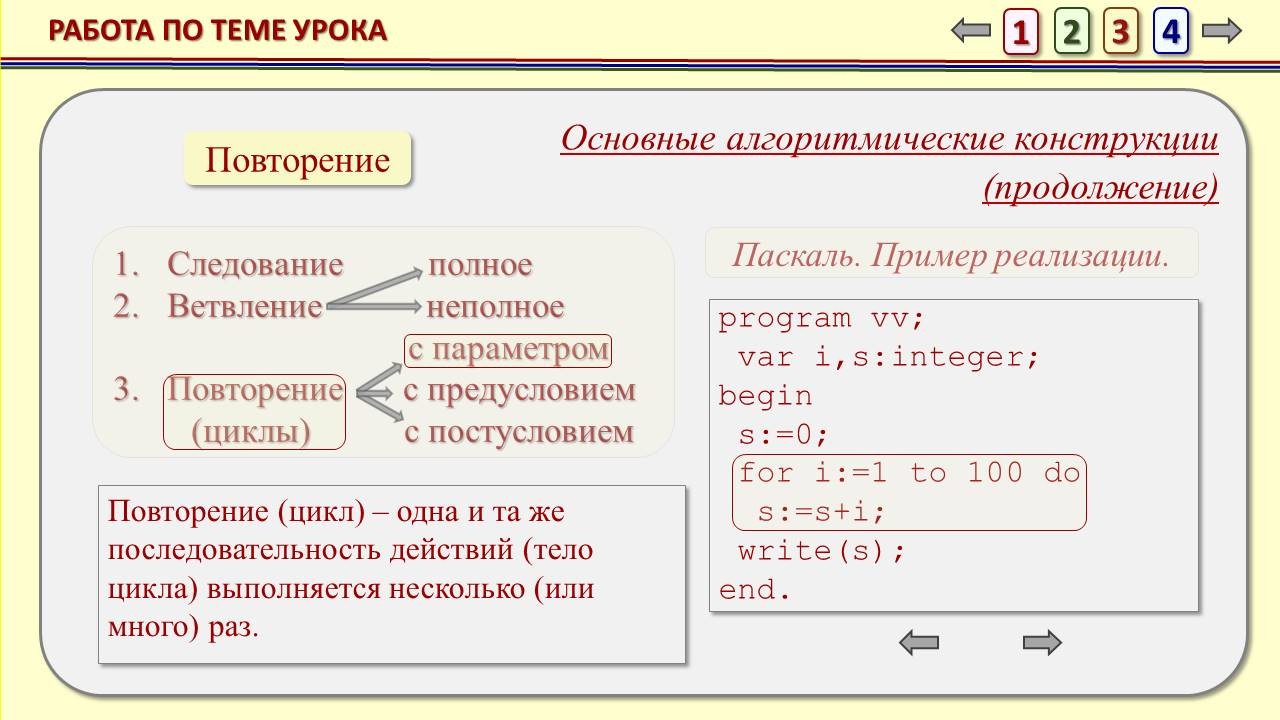
Учитель информатики: А сейчас, прежде, чем перейти непосредственно к составлению программы, давайте кратко вспомним основные алгоритмические конструкции и их реализацию на языке Паскаль, а также структуру программы.

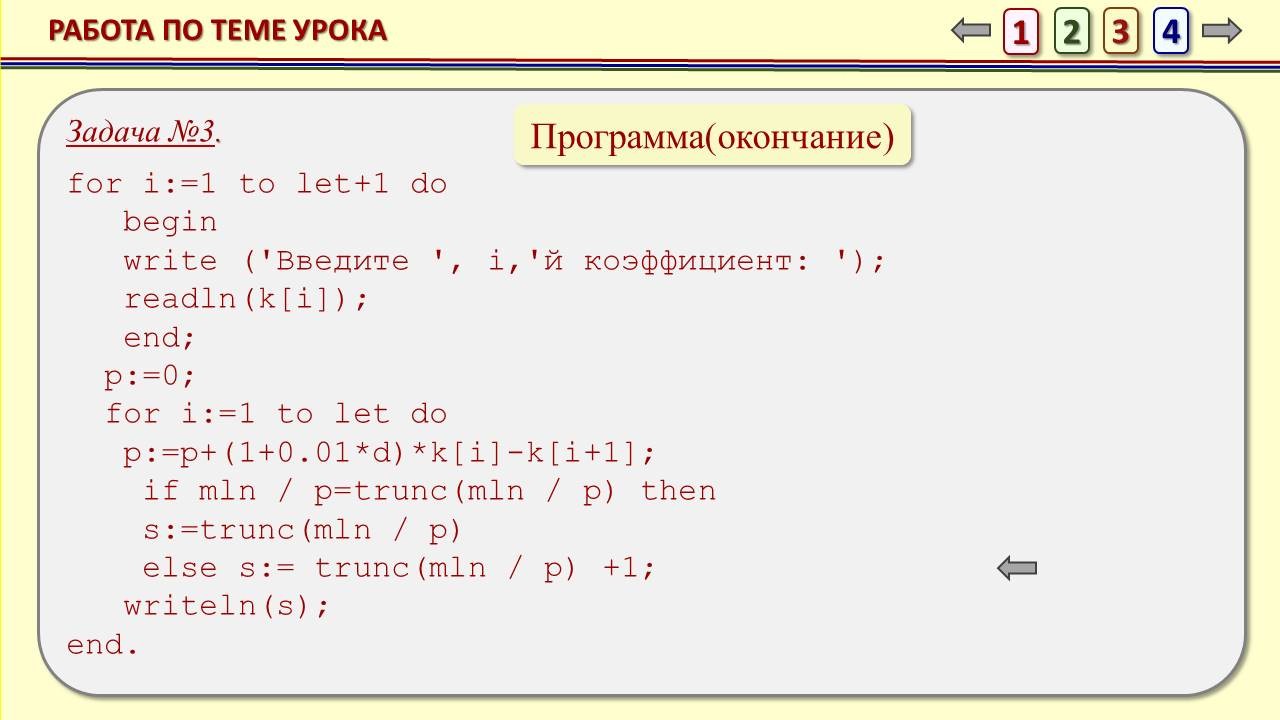
Задача №3

В начале января 2018 года планируется взять кредит в банке на 4 года на S млн. рублей, где S – целое число. Условия его возврата таковы:

- каждый июль долг возрастает на 10% по сравнению с началом текущего года;

- с августа по декабрь каждого года необходимо выплатить часть долга;

- в январе каждого года долг должен составлять часть кредита в соответствии со следующей таблицей:

Найдите наименьшее значение S, при котором сумма выплат банку за все четыре года составит не менее 10 миллионов рублей.

Решение:

Так как долг на январь 2019 года должен составлять 0,8S, то 1 платеж будет равен: 1,1S-0,8S=0,3S.

Долг на январь 2020 года должен составлять 0,5S, то  2 платеж будет равен: 1,1 ∙ 0,8S – 0,5S=0,88S-0,5S=0,38S.

Долг на январь 2021 года должен составлять 0,3S, то 3 платеж будет равен: 1,1∙0,5S-0,3S=0,55S-0,3S=0,25S.

Так как долг на январь 2022 года должен составлять 0, то 4 платеж будет равен: 1,1 ∙ 0,3S-0S=0,33S.

Тогда общая сумма выплат банку составит: (0,3+0,38+0,25+0,33)∙S=1,26S.

По условию задачи эта сумма должна составлять не менее 10 миллионов рублей, то есть

Ответ: 8.

Домашнее задание

Учитель математики: Решите данную экономическую задачу, напоминаю, что необходимо составить математическую модель задачи, а затем решить ее.

Учитель информатики: А также составьте программу для этой задачи, используя составленную математическую модель.

Задача

В июне планируется взять кредит в банке на сумму 5 млн.рублей на некоторый срок (целое число лет). Условия возврата таковы:

- каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;

- с февраля по май каждого года должен быть на одну и ту же сумму меньше долга на июнь предыдущего года.

На сколько лет был взят кредит, если известно, что сумма выплат банку сверх взятого кредита после его полного погашения составила 3 млн.рублей?

Решение:

n – число лет, на сколько взят кредит; а (руб.) – сумма кредита (в задаче а=5).
Если кредит берется на 1 год, то 0,1а=0,5;

Ответ: 11 лет.