Слайд 2
Цель: знакомство с листом Мебиуса как объектом топологии.
Слайд 3
Задачи:
Образовательные:
- рассказать учащимся о математике А.Ф. Мёбиусе и его изобретении, познакомить с одной из областей математики – топологией;
- сформулировать свойства листа Мебиуса;
- рассмотреть применение листа Мебиуса на практике;
Развивающие:
- развивать логическое мышление;
- развивать навык самостоятельной работы при проведении исследования;
- развивать умения выдвигать гипотезу и сопоставлять ее с полученным результатом;
Воспитательные:
- воспитывать целеустремленность в достижении цели;
- прививать интерес к математике, математическим опытам;
- воспитывать коллективизм, взаимопомощь.
Оборудование: экран, проектор, бумажные ленты, ножницы, клей, краски (цветные карандаши, фломастеры).
Ход занятия
1. Орг.момент
Добрый день. Сегодня наш урок-эксперимент будет посвящен изобретению великого геометра А.Ф. Мёбиуса, которому в этом году исполняется 225 лет.
2. Изучение нового материала
Слайд 4
Как вы думаете, если космический корабль полетит все время прямо, никуда не сворачивая, то будет ли он все более удаляться от Земли?
(ответы учащихся)
"Не обязательно, - решил Эйнштейн. - Корабль может вернуться, даже если он все время будет лететь прямо".
Такой путь космического корабля нам поможет представить лента (лист, петля) Мёбиуса.
Слайд 5
Таинственный и знаменитый лист Мёбиуса придумал в 1858 г. немецкий геометр Август Фердинанд Мёбиус (1790-1868), ученик “короля математиков” Гаусса. Мёбиус был первоначально астрономом, как Гаусс и многие другие из тех, кому математика обязана своим развитием. В те времена занятия математикой не встречали поддержки, а астрономия давала достаточно денег, чтобы не думать о них, и оставляла время для собственных размышлений. И Мёбиус стал одним из крупнейших геометров 19 в. В возрасте 68 лет ему удалось сделать открытие поразительной красоты. Это открытие односторонних поверхностей, одна из которых - лист Мёбиуса.
Слайд 6
Лист Мебиуса считается одним из символов современной математики, а момент его открытия стал началом рождения новой науки – топологии. В некотором смысле слово топология – это наука, изучающая непрерывность.
Слайд 7
Тополог интересуется свойствами “предметов”, которые выдерживают деформации: сжатия и растяжения (как если бы они были сделаны из резины). С точки зрения топологии баранка и кружка – это одно и то же.
Сжимая и растягивая кусок резины, можно перейти от одного из этих тел ко второму. А вот баранка и шар – разные объекты: чтобы сделать отверстие, надо разорвать резину.
Вот такая интересная и занимательная наука топология.
Говорят, что открыть свой “лист” Мебиусу помогла служанка, сшившая однажды неправильно концы ленты.
3. Лабораторная работа
Давайте рассмотрим, что же такое лист Мёбиуса?
Как вы думаете, существует ли одежда без изнанки? Конечно же, нет. Давайте рассмотрим кольцо. Оно представляет собой двухстороннюю поверхность. Если двигаться по одной стороне кольца, то не “пересекая границы” нельзя очутиться на другой его стороне. Другое дело – лента Мёбиуса.
Слайд 8
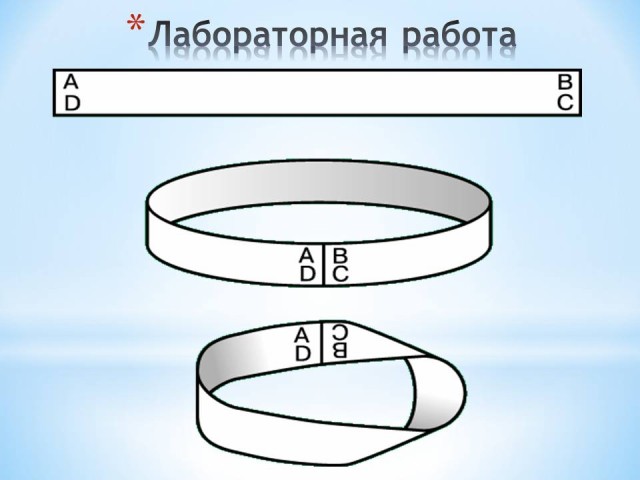
Возьмите в руки бумажную ленту АВСD, разделённую пополам пунктирной линией.
Приложите её концы АD и ВС и склеиваю. Но не как попало, а так, чтобы точка А совпала с точкой С , а точка В с D. Для этого перед склейкой перекрутите ленту один раз. Получилось знаменитое в математике бумажное кольцо. Лист Мёбиуса готов.
Эксперимент 1. “Отрежь кусочек”.
Теперь разрежем ножницами склеенную ленту посередине вдоль пунктирной линии. Как вы думаете, что у нас получится? Конечно, если бы мы не перекрутили ленту перед склейкой, всё было бы просто: из одного широкого кольца получилось бы два узких. А что сейчас? Получилось не два кольца, а одно, но зато вдвое длиннее. К тому же перекручено оно не один раз, а два.
А ну-ка, разрежем это кольцо ещё раз посредине. Получится два сцепленных друг с другом кольца, каждое из которых дважды перекручено. Вот какие неожиданные вещи происходят с простой бумажной полоской, если склеить из неё лист Мёбиуса.
У этого листа масса удивительных свойств. Сейчас вы в этом убедитесь. Сколько сторон у листа Мёбиуса? У ленты, из которой сделан лист Мёбиуса, имеется две стороны. А у него самого, оказывается, есть только одна сторона!
Эксперимент 2. “Ученик - перевертыш”.
Возьмем ручку и представим что это вовсе не ручка, а вы сами. И вы пошли гулять вдоль пунктира, идущего посередине листа Мёбиуса. И вот вы шли, шли и вернулись к месту старта. Но в каком виде! В перевернутом! Что надо сделать, чтобы вернуться к месту старта в нормальном положении. Точно нужно совершить еще одно “кругосветное” путешествие. Проверим!
Эксперимент 3. “Сколько сторон у листа Мёбиуса?”
Возьмите лист Мёбиуса, обмакните кисть в зелёную краску и начинайте красить, кладя каждый новый мазок так, чтобы он прилегал к прежним. Только не переходите через край ленты! Если бы лента не была перекручена, то через некоторое время одна сторона кольца оказалась бы полностью зелёной, а другая осталась белой. А как с листом Мёбиуса? Вы закрасите его весь!
Слайд 9
“Если кто-нибудь вздумает раскрасить только одну сторону поверхности мёбиусовой ленты, пусть лучше сразу погрузит её всю в ведро с краской”, - пишут Рихард Курант и Герберт Роббинс в превосходной книге “Что такое математика?”.
Если на внутреннюю сторону обычного кольца посадить паука, а на наружнюю - муху и разрешить им ползать как угодно, запретив лишь перелезать через края кольца, то паук не сможет добраться до мухи, не так ли? А если их обоих посадить на лист Мёбиуса, то бедная муха будет съедена (если, конечно, паук ползает быстрее мухи!)
Близкой к ленте Мёбиуса односторонней поверхностью является бутылка Клейна.
Слайд 10 Бутылка Клейна может быть получена путём склеивания двух лент Мёбиуса по краям. В обычном трёхмерном пространстве сделать это, не создавая самопересечения, невозможно.
4. Самостоятельная работа
Слайд 11 Дополнительное задание
- Группа 1 - Что получится, если перекрутить ленту дважды, а затем разрезать вдоль посередине?
- Группа 2 - Что получится, если разрезать вдоль лист Мёбиуса, по всей длине на три равные части?
Слайд 12 Проверка самостоятельной работы
5. Подведение итогов
- Слайд 13 Лист Мёбиуса используется во многих изобретениях, навеянных тщательным изучением свойств односторонней поверхности.
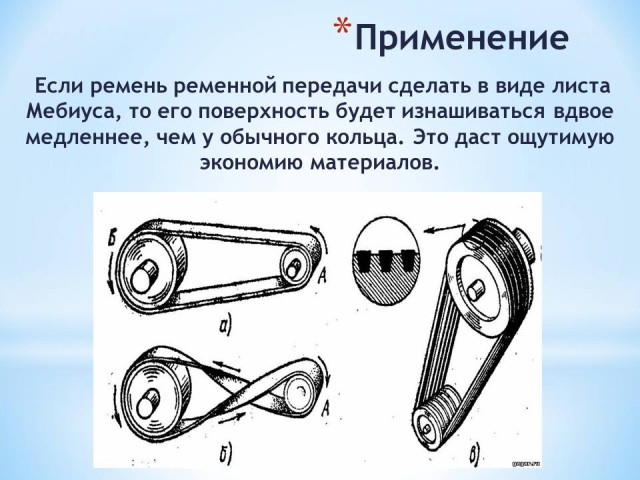
- Слайд 14 Полоса ленточного конвейера, выполненная в виде листа Мёбиуса, позволяет ему работать дольше в два раза, потому что вся поверхность листа равномерно изнашивается. Слайд 15
- Слайд 16 В матричных принтерах красящая лента имеет вид листа Мёбиуса для увеличения её ресурса. Это даёт ощутимую экономию.
- Слайд 17 Физики предполагают, что наша Вселенная вполне вероятно замкнута в ту же самую ленту согласно теории относительности Эйнштейна и его предположением, что космический корабль, всё время летящий прямо, может вернуться к месту старта, что подтверждает неограниченность Вселенной.
- Слайд 18 Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мебиуса и только поэтому генетический код так сложен для расшифровки и восприятия. Больше того – такая структура вполне логично объясняет причину наступления биологической смерти – спираль замыкается сама на себя и происходит самоуничтожение.
- Слайд 19 Лист Мебиуса удивительная поверхность и притягивает к себе внимание не только математиков, но и людей искусства. Слайд 20 Нередко изображение ленты Мёбиуса используется художниками в картинах, Слайд 21 картинах-иллюзиях. Слайд 22 Скульпторы также обращают внимание на необычную ленту. Архитекторы при строительстве объектов зачастую используют эту необычную изогнутую форму. Слайд 23, 24
- Слайд 25 В быту, в модных вещах, при изготовлении украшений не обходится без ленты Мёбиуса
- Слайд 26 Знак вторичной переработки, используемый по всему миру так же представляет собой ленту Мёбиуса – знак бесконечности.
6. Домашнее задание.
Слайд 27
Что получится, если ленту перекрутить на три оборота и склеить. Проведите опыт самостоятельно:
- Взять не бумажную ленту, а полосу любой ткани.
- Повернуть один из концов полоски на три оборота, т.е. на 540 градусов.
- Сшить оба конца.
- Теперь возьмите ножницы и аккуратно разрежьте полоску посередине. Посмотрите, что получится.
7. Вывод
Слайд 28
В настоящее время многие изобретатели
пользуются свойствами данной ленты для
проведения экспериментов и создания новых
устройств.
Лента Мебиуса продолжает вызывать стойкий
интерес, не только у математиков и изобретателей,
но и у обычных людей. Она вдохновляет деятелей
искусства на создание загадочных произведений и
фантастических теорий. Эксперименты с этой
интересной фигурой – увлекательное занятие, как
для взрослого, так и для ребенка. Ее свойства
нашли свое применение в науке, технике и в быту.
Лента Мебиуса - это занимательная математическая
загадка, скрывающая в себе смысл
идеалистического понимания устройства
Вселенной, ее воздействие на нашу жизнь можно
изучать бесконечно.
Источники:
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. Книга для учащихся 5-6 классов. М.: Просвещение, 1998.
- Перельман Я.И. Занимательная геометрия. М.: Римис, 2014.
- Шарыгин И. Ф., Ерганжиева Н.Н. Наглядная геометрия. М.: Дрофа, 2012г.
- http://infourok.ru/urok_-_laboratornaya_rabota_list_mebiusa-376783.htm
- http://doc4web.ru/matematika/konspekt-uroka-po-matematike-list-mebiusa-klass.html
- http://doc4web.ru/matematika/tehnologicheskaya-karta-uroka-po-matematike-topologicheskie-opit.html
- http://globuss24.ru/doc/vneklassnoe-meropriyatie-udivitelyniy-list-mebiusa-7-klass
- https://urok.1sept.ru/articles/635808/
- https://urok.1sept.ru/articles/553801/
- http://infourok.ru/material.html?mid=16752
- http://sc50.jdroo.by/index.php?option=com_content&view=article&id=401%3A-q-q&catid=53%3A2014-03-07-11-57-49&Itemid=118&lang=ru
- http://nsportal.ru/shkola/geometriya/library/2012/04/08/tainstvennyy-list-myobiusa
- http://www.calculator888.ru/blog/raznoe/lenta-mebiusa.html
- http://sbatal.jimdo.com/%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5/
- http://vestnik-nou1.narod.ru/primenenie_lista_mebiusa_2.htm
- http://buckses.info/fizika/
- http://stasy-egorova.pldetstva.edusite.ru/p70aa1.html