Урок на тему «Внешний угол треугольника и его свойство»
Цели.
Знакомство учащихся с понятием внешнего угла треугольника, с формулировкой определения; рассмотреть свойство внешнего угла треугольника; закрепить знания учащихся о сумме углов треугольника и о внешнем угле треугольника при решении задач.
Задачи.
1. Обучающая: обеспечить усвоение материала всеми учащимися; учить и научить каждого ученика самостоятельно добывать знания; формировать навыки, умения, которые обеспечивают успешное выполнение деятельности.
2. Развивающая: способствовать развитию математического кругозора, мышления: умения анализировать, выделять главное, сравнивать, обобщать и систематизировать, развивать устную и письменную речи, внимание и память; продолжить работу по развитию умения самостоятельно приобретать новые знания; использование для достижения поставленной задачи уже полученных знаний.
3. Воспитывающая: содействовать воспитанию интереса к математике, активности, дисциплинированности, честности, ответственности за свой труд и труд одноклассника, воспитание навыков самоконтроля и взаимоконтроля.
Оборудование:
- линейка, карандаш, треугольник;
- компьютер, мультимедийный проектор, интерактивная доска;
- презентация.
Литература
- Учебник Геометрия 7-9 классы: учеб. для общеобразоват. учреждений Л.С. Атанасян, В.Ф. Бутузов.
- Уроки геометрии с применением информационных технологий. 7-9 классы. Методическое пособие с электронным приложением, / Е.М.Савченко. - 2-е издание, стереотипное. Москва "Планета", 2012.
Ход урока
I. Организационный момент
ІI. Активизация познавательной деятельности
- Один из учащихся доказывает теорему о сумме углов треугольника.
- Второй учащийся решает на доске задачу № 230.
- Устно со всем классом решаем задачи по готовым чертежам.
Вычислить все неизвестные углы треугольника
- Найдите неизвестный угол треугольника, если у него два угла равны 50° и 60°. (Слайд 2, рисунок 1). Презентация
- Найдите неизвестный угол треугольника, если у него один угол прямой, а другой равен 20°. (Слайд 2, рисунок 2)
- Найдите угол при основании равнобедренного треугольника, если угол между боковыми сторонами 40°. (Слайд 2, рисунок 3)
- Найдите угол между боковыми сторонами равнобедренного треугольника, если угол при основании у него равен 30°. (Слайд 2, рисунок 4)
- Вычислить все неизвестные углы прямоугольного равнобедренного треугольника. (Слайд 3, рисунок 1)
- Вычислить все неизвестные углы равностороннего треугольника. (Слайд 3, рисунок 2)
- Вычислите все неизвестные углы треугольников (Слайд 4)
- Определите вид треугольника (Слайды 5, 6, 7)
III. Изучение нового материала.
Вступительное слово учителя (постановка проблемы урока).
Ребята, сегодня перед нами стоит такая проблема: нам нужно познакомиться ещё с одним углом, с которым мы раньше не встречались, у которого так же есть своё свойство. Мы сегодня повторили многие углы, которые мы знаем, и некоторые из них помогут нам в решении нашей поставленной задачи.
1. Ввести понятие внешнего угла треугольника:
Ребята, давайте выполним следующую практическую работу, а именно:
- Постройте произвольный треугольник АВС
- Проведите луч ВД так, чтобы полученный угол был смежным с углом В треугольника АВС.
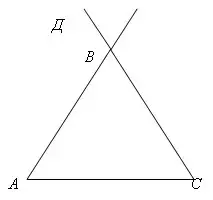
- Назовите получившийся угол (может быть два варианта
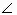 АВД или
АВД или 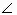 СВД)
СВД) - Где они лежат по отношению к треугольнику, внутри или вне его?
- Эти углы имеют специальное название - они называются внешними углами треугольника.
- А теперь запишем тему урока "Внешний угол треугольника и его свойство"
- А как вы думаете, можно ли при других вершинах этого треугольника построить внешние углы?
- Итак, попробуем сформулировать определение внешнего угла треугольника.
Вывод: Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
IV. Физкультминутка.
а) Дыхательное упражнение.
б) Упражнение для позвоночника.
в) Упражнение для глаз.
- Что мы знаем об углах треугольника? (
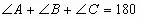 °)
°) - Что мы знаем о смежных углах? (Сумма смежных углов равна 180° или
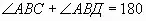 °)
°) - Посмотрите на эти равенство повнимательнее и скажите , что из них следует? (
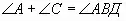 )
) - Какой можно сделать вывод?
Вывод: Внешний угол треугольника равен сумме двух других углов треугольника, не смежных с ним.
Это и есть свойство внешнего угла треугольника, и мы его вместе доказали.
V. Решение задач
1. Устно решить задачу: в треугольнике АВС ![]() =110°.
=110°.
Чему равны:
а) сумма остальных внутренних углов треугольника?
б) внешний угол при вершине С?
2. По готовому чертежу на доске устно решить задачу:
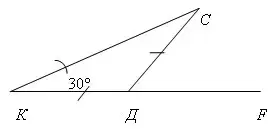
Найдите внутренние и внешний угол СДF треугольника КСД.
3. Решить задачу № 232 под руководством учителя на доске и в тетрадях.
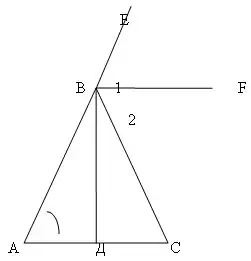
Дано: ![]() внешний угол треугольника АВС;
внешний угол треугольника АВС; ![]() .
.
Доказать: ![]() равнобедренный.
равнобедренный.
Решение
Проведем биссектрисы ВF и ВД смежных углов СВЕ и АВС, тогда ВF || АС, так как ![]() , а углы
1 и А соответственные при пересечении прямых ВF и АС секущей АВ, ВД
, а углы
1 и А соответственные при пересечении прямых ВF и АС секущей АВ, ВД ![]() , так как ВД
, так как ВД ![]() , а BF || AC.
, а BF || AC.
В треугольнике АВС биссектриса ВД является высотой, следовательно, треугольник АВС - равнобедренный (см. задачу № 133)
2. Обратное утверждение также верно, а именно: если треугольник равнобедренный, то внешний угол при вершине, противолежащей основанию треугольника, в два раза больше угла при основанию Действительно, этот внешний угол равен сумме двух углов при основании равнобедренного треугольника, с так как углы при основании равны, то данный внешний угол в два раза больше угла при основании треугольника.
VI. Самостоятельная работа обучающего характера (на четыре варианта)
Вариант 1
1. Один из углов равнобедренного треугольника равен 96°. Найдите два других угла.
2. В треугольнике СДЕ с углом ![]() проведена биссектриса СF,
проведена биссектриса СF, ![]() . Найдите
. Найдите ![]()
Вариант 2
1. Один из углов равнобедренного треугольника равен 108°. Найдите два других угла.
2. В треугольнике СДЕ проведена биссектриса СF, ![]() ,
,![]() .
.
Найдите ![]()
Вариант 3
1. В равнобедренном треугольнике МNP c основанием MP и углом ![]() проведена высота MH. Найдите
проведена высота MH. Найдите ![]() .
.
2. В треугольнике СДЕ проведены биссектрисы СК и ДР, пересекающиеся в точке F, причем ![]() Найдите
Найдите ![]()
Вариант 4
1. В равнобедренном треугольнике СДЕ c основанием СЕ и углом ![]() проведена высота СH. Найдите
проведена высота СH. Найдите ![]() .
.
2. В треугольнике АВС проведены биссектрисы АМ и BN, пересекающиеся в точке K, причем ![]() Найдите
Найдите ![]()
VII. Домашнее задание: изучить пункты 30-31; ответить на вопросы 1-5 на стр. 84; решить задачи № 233, 235.
VIII. Итоги урока
С чем мы сегодня познакомились?
- Что такое внешний угол треугольника?
- Какое свойство внешнего угла мы сегодня доказали?
- Чему вы сегодня научились?
- Какие теоремы сегодня на уроке мы использовали при решении задач?
IX. Рефлексия