Открытый урок по теме "Синус, косинус, тангенс и котангенс"
Скачать презентацию (2.16 МБ)
Цели урока:
- Образовательные: ввести понятие тригонометрических функций синуса, косинуса, тангенса и котангенса, как координат точки единичной окружности; определить множество значении этих функций; рассмотреть перевод градусной меры измерения улов в радианную меру и наоборот; сформировать умение определять знаки тригонометрических функций; рассмотреть зависимости между косинусом, синусом, тангенсом и котангенсом одного и того же аргумента; научить находить значения тригонометрических функций по тригонометрической окружности выполнять действия с тригонометрическими функциями.
- Развивающие: развивать и совершенствовать умения применять имеющиеся у учащихся знания в различных ситуациях; развивать грамотную математическую речь учащихся, умение давать лаконичные формулировки.
- Воспитательные: воспитывать у учащихся аккуратность, умение слушать, высказывать свое мнение; культуру поведения.
Тип урока: комбинированный.
Форма работы: фронтальная и индивидуальная.
Методы обучения: диалогическое изложение материала с использованием ИКТ.
Оборудование: компьютер, мультимедийный проектор, раздаточный материал, презентация к уроку.
Ход урока
I. Организационный момент. (2 мин.)
Проверить готовность группы и кабинета к уроку. Настроить учащихся на тему урока.
Открываем тетради. Записываем сегодняшнее число и тему нашего урока: «Синус, косинус, тангенс, котангенс».
Все новое и необычное всегда привлекает к себе и люди, пусть даже неосознанно, стремятся это узнать. Таджикский поэт Рудаки так говорил об этом:
С тех пор как существует мирозданье,
Такого нет, кто б ни нуждался в знанье.
Какой мы ни возьмем язык и век,
Всегда стремится к знанью человек!
Сегодня мы начинаем изучать тригонометрию. Тригонометрия - это греческое слово и в переводе означает измерение треугольников. Возникновение тригонометрии было связано сземле измерением, астрономией, строительным делом. Выходит, что знание и понимание этой темы важно не только для будущей сдачи экзамена по математике, но для освоения и выбранной вами профессией.
II. Активизация знаний. (3 мин.)
С этим разделом математики вас познакомили учителя на уроках геометрии при изучении отношений между сторонами и углами в прямоугольном треугольнике.
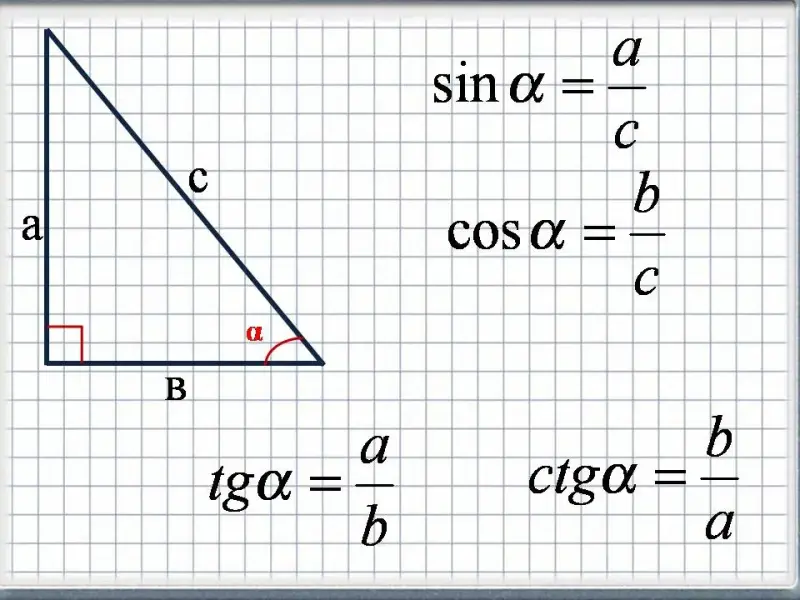
Давайте вспомним: какие понятий связывают стороны и острые углы прямоугольного треугольника?
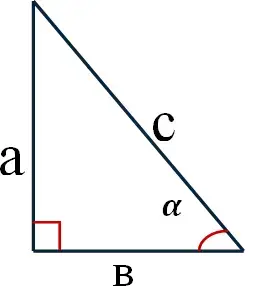
Итак, синус, косинус, тангенс и котангенс - это некоторые числа. Причем для каждого угла свои и их значение зависит только от величины угла.
Также вам уже известно, что синус, косинус, тангенс и котангенс называют тригонометрическими функциями, и мы можем их найти по величине угла или наоборот найти величину угла, если нам известно значение одной из этих функций. Для этого существуют специальные таблицы Брадиса. Правда, в настоящее время мы обращаемся к ним редко, а скажите почему?
III. Историческая справка. (2 мин.)
Понятие синуса угла, как отношение отрезков треугольника появилось уже 3 веке до нашей эры в работах математиков Древней Греции - Евклида, Архимеда, Апполония Пергского. В 1 веке нашей эры оно исследовалось Минелаем, но еще не получило своего сегодняшнего названия. В 4-5 веках индийский ученый Ариабхаты ввел специальный термин джива - «тетива», который при переводе арабских текстов на латынь был заменен синусом, что означает изгиб, кривизна.
Слово косинус намного моложе. Косинус - это сокращение латинского выражения, которое означает «дополнительный синус».
Абу-Абдалах, арабский астроном и математик 10 века, наблюдая за солнечными часами, создал первые таблицы таких тригонометрических функций, как тангенс и котангенс, не вводя эти понятия. Сам термин, в переводе с латинского означающий «отрезок касательной» был введен только в 1583 году датским математиком Томасом Финком.
IV. Изложение нового материала. (25 мин.)
Сегодня на уроке мы продолжим изучать эти тригонометрические функции, а также познакомимся с тригонометрической окружностью, рассмотрим понятие этих функций с помощью окружности, научимся находить по ней значения функций, их знаки, вспомним основные тригонометрические тождества и разберем, как их применять для решения задач.
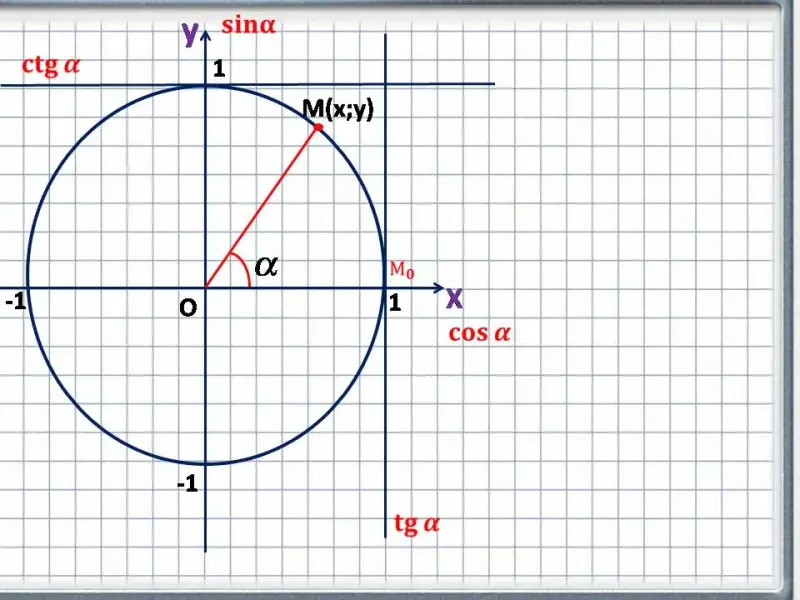
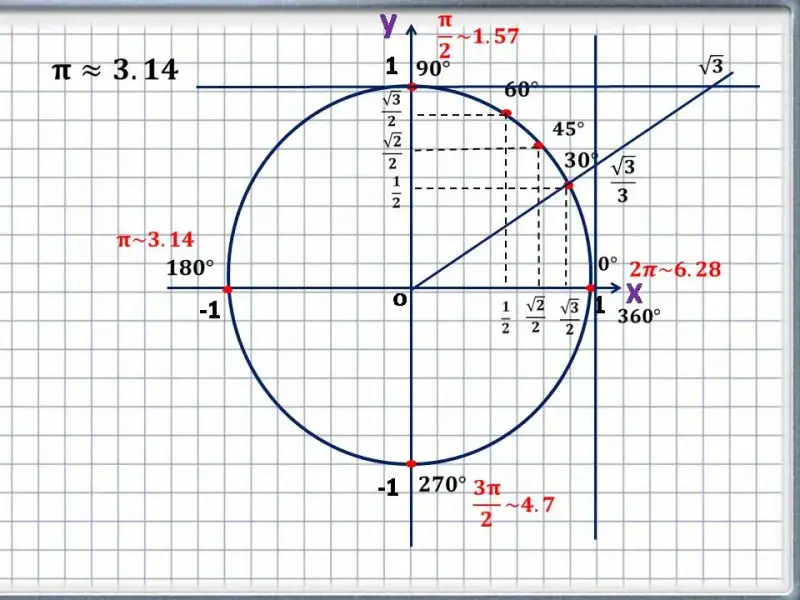
Рассмотрим окружность единичного радиуса центр, которой совпадает с началом прямоугольной системы координат. Это означает, что у нас есть знакомые нам ось абсцисс (ось х) и ось ординат (ось у).
Центр окружности мы совместили с началом координат. Наша окружность единичная, то есть радиус у нее равен 1. Значит, координаты точек пересечения с окружностью будут равны 1 и -1 на каждой оси.
Возьмем точку с координатами (1;0), которая будет двигаться по нашей окружности, обозначим ее ![]() . За положительное направление
выбирают движение против часовой стрелки, за отрицательное движение по часовой стрелке. Начальное положение, которое занимает наша точка, примем за начало отсчета пути, пройденного точкой по
окружности. Пусть точка двигается против часовой стрелки, то есть в положительном направлении. При движении по окружности она займет положение точки М, которая будет иметь координаты (х; у), так как
точка расположена в координатной плоскости. Проведем к этой точке радиус и угол между этой точкой М и радиусом обозначим
. За положительное направление
выбирают движение против часовой стрелки, за отрицательное движение по часовой стрелке. Начальное положение, которое занимает наша точка, примем за начало отсчета пути, пройденного точкой по
окружности. Пусть точка двигается против часовой стрелки, то есть в положительном направлении. При движении по окружности она займет положение точки М, которая будет иметь координаты (х; у), так как
точка расположена в координатной плоскости. Проведем к этой точке радиус и угол между этой точкой М и радиусом обозначим ![]() .
Значит, положение точки М мы можем задать двумя способами: с одной стороны координатами (х; у), так как точка лежит в координатной плоскости и с другой стороны с помощью угла поворота этой точки
вокруг начала координат. И если мы можем положение точки задать двумя способами, значит между ними, должна быть какая-то связь. То есть координаты точки (х; у) и величина угла должны быть связаны
некоторой функцией. Таким образом, у нас появляются тригонометрические функции, которые выражают зависимость между координатами точки единичной окружности в системе координат и углом поворота, при
помощи которого мы попадаем из нашей начальной точки
.
Значит, положение точки М мы можем задать двумя способами: с одной стороны координатами (х; у), так как точка лежит в координатной плоскости и с другой стороны с помощью угла поворота этой точки
вокруг начала координат. И если мы можем положение точки задать двумя способами, значит между ними, должна быть какая-то связь. То есть координаты точки (х; у) и величина угла должны быть связаны
некоторой функцией. Таким образом, у нас появляются тригонометрические функции, которые выражают зависимость между координатами точки единичной окружности в системе координат и углом поворота, при
помощи которого мы попадаем из нашей начальной точки ![]() при движении, в точку М. Выразим эту зависимость, определяя,
координаты точки М. Опускаем перпендикуляры на координатные оси. Получаем прямоугольный треугольник.
при движении, в точку М. Выразим эту зависимость, определяя,
координаты точки М. Опускаем перпендикуляры на координатные оси. Получаем прямоугольный треугольник.
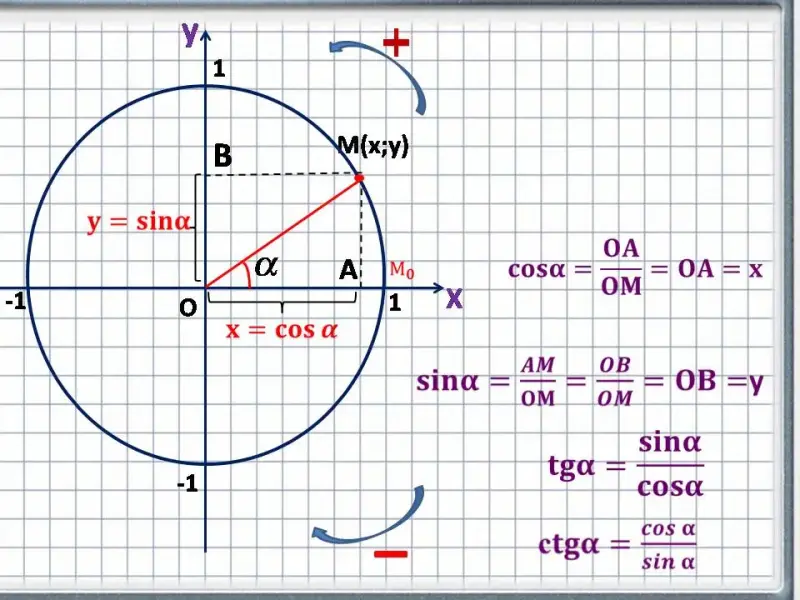
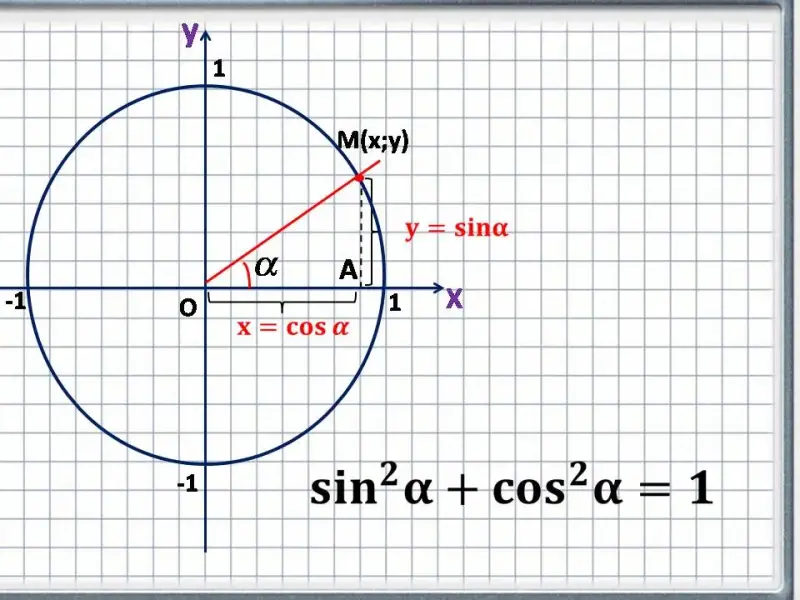
Применим уже известные нам отношения между сторонами и углами прямоугольного треугольника и получим, что координата х (абсцисса) точки М будет равна:
,
. Так как у нас единичная окружность, то ОМ=1. Ордината у точки М находится аналогично и будет равна:
, у=
Для функций тангенс и котангенс получаем следующие равенства из того же прямоугольного треугольника: ![]()
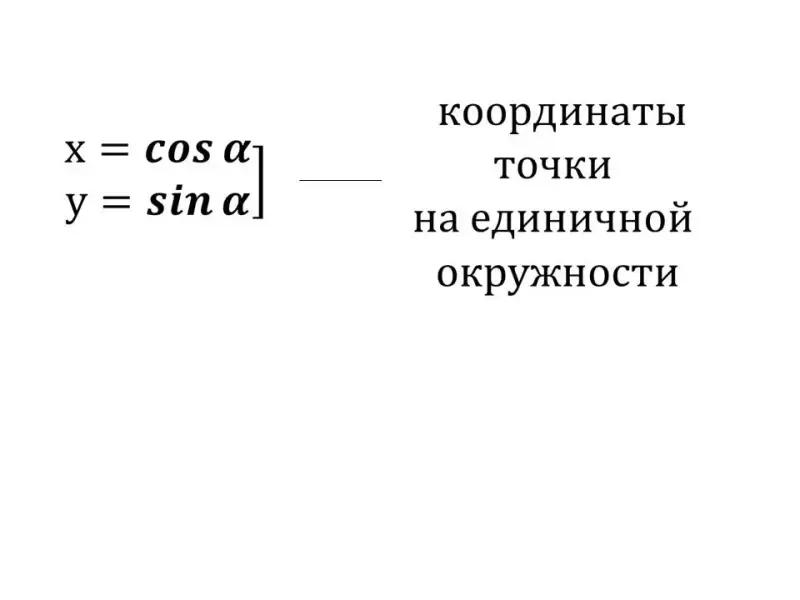
Итак, косинусом угла α называется абсцисса (то есть координата по оси OX) точки на единичной окружности, соответствующей данному углу α.
Синусом угла α называется ордината (то есть координата по оси OY ) точки на единичной окружности, соответствующей данному углу α.
Получаем, что ось х - это ось косинуса, ось у - это ось тангенса. Функции тангенс и котангенс также имеют свои оси. Осью тангенсов является касательная к единичной окружности в точке с координатой (1; 0), а осью котангенсов - касательная к окружности в точке с координатой (0; 1) и значит значения этих функций находят по данным осям.
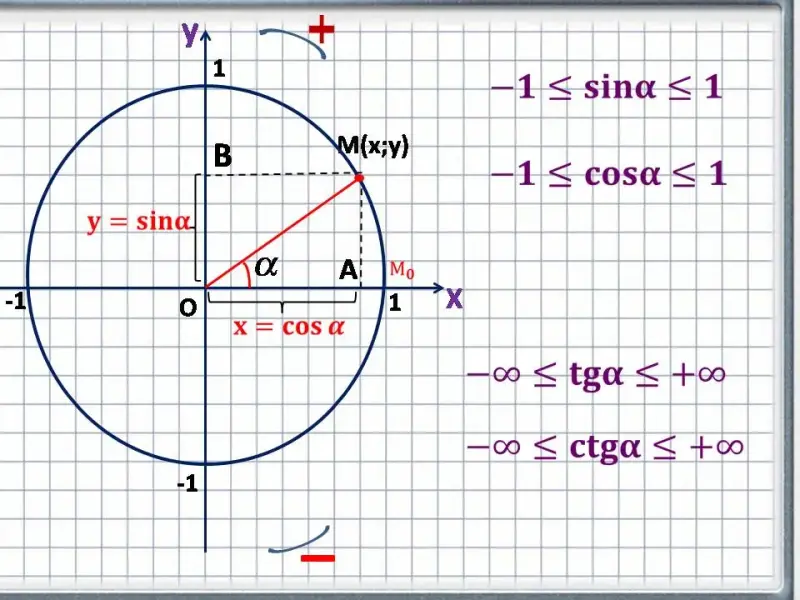
Так как синус и косину это по сути координаты точки на единичной окружности и из ее рассмотрения видно, что они лежат в пределах от -1 до 1, то можем сделать вывод, о том какие значения могут
принимать наши функции: ![]()
Зная это мы, можем ответить на вопрос: может ли ![]() .
.
Значение угла ![]() может быть любым: отминус бесконечности до плюс бесконечности.
может быть любым: отминус бесконечности до плюс бесконечности.
Обратимся к нашему треугольнику и вспомним теорему Пифагора. Радиус единичной окружности - это гипотенуза треугольника, а ее катеты равны соответственно ![]() и
и ![]() . Тогда применяя теорему Пифагора (квадрат гипотенузы прямоугольного треугольника равен сумме
квадратов ее катетов) получаем равенство, называемое основным тригонометрическим тождеством:
. Тогда применяя теорему Пифагора (квадрат гипотенузы прямоугольного треугольника равен сумме
квадратов ее катетов) получаем равенство, называемое основным тригонометрическим тождеством: ![]()
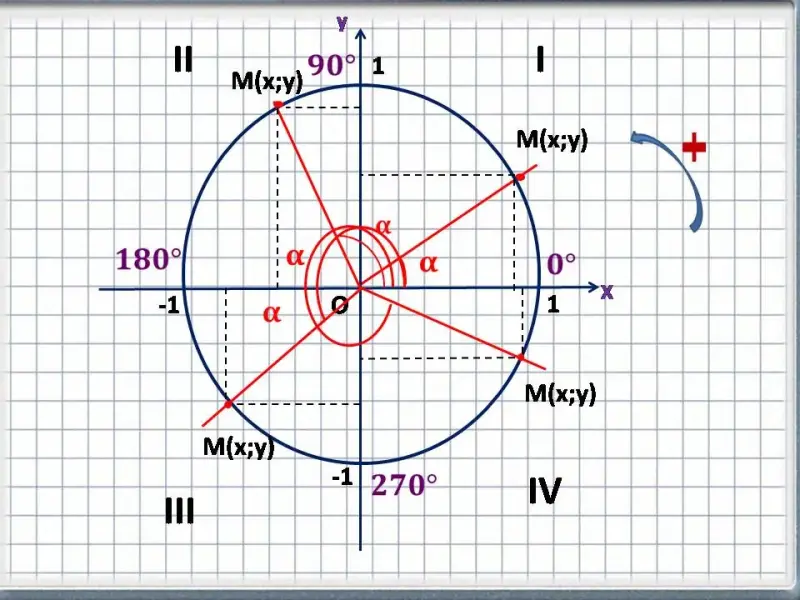
А сейчас давайте разберемся, как нам определять знаки тригонометрических функций. Это не сложно. Знаки тригонометрических функций соответствуют знакам координат точки единичной окружности.
Координатные оси разбивают всю координатную плоскость и окружность на четыре координатные четверти. Нумерация четвертей совпадает с началом движения точки ![]() по окружности в положительном направлении, то есть против часовой стрелки. (далее указываем по рисунку номера четвертей). Границы наших четвертей: от точки
по окружности в положительном направлении, то есть против часовой стрелки. (далее указываем по рисунку номера четвертей). Границы наших четвертей: от точки ![]() - это
- это ![]() до
до ![]() , от
, от ![]() до
до ![]() , от
, от ![]() до
до ![]() , от
, от![]() до
до ![]() .
.
Определим знаки тригонометрических функций в каждой четверти, для этого заполним таблицу:
| I | II | III | IV | |
| + | + | - | - | |
| + | - | - | + | |
| + | - | + | - | |
| + | - | + | - |
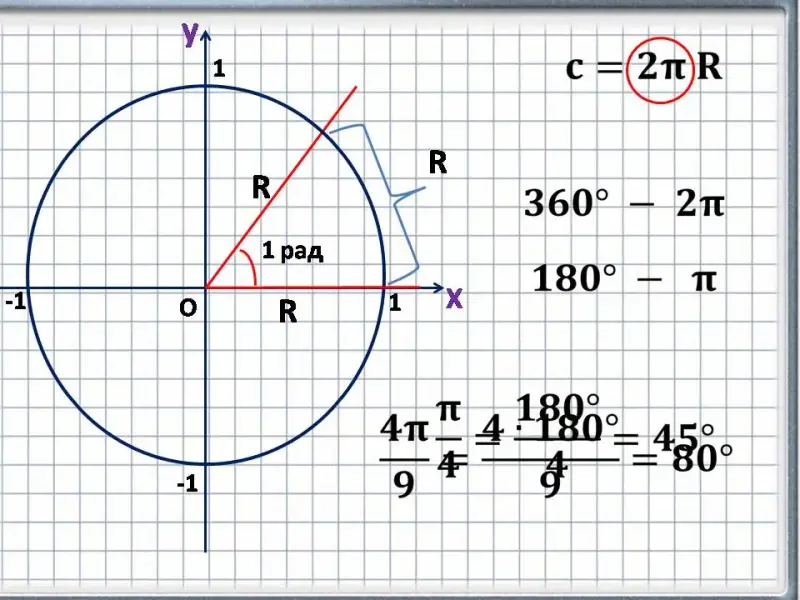
Вы уже знаете, что величины углов могут измеряться в радианной мере и градусной мере. А. А это означает, что вы должны уметь переходить от радианной меры измерения угла к градусной.
Углом в 1 радиан это центральный угол, который опирается на дугу, равную радиусу. Длина окружности равна: ![]() . То есть в нашей
окружности помещается ровно два пи дуг длина которых равна радиусу и значит, во всей нашей окружности помещается два пи углов в один радиан. Вся окружность равна
. То есть в нашей
окружности помещается ровно два пи дуг длина которых равна радиусу и значит, во всей нашей окружности помещается два пи углов в один радиан. Вся окружность равна ![]() . Значит,
. Значит,![]() соответствует
соответствует ![]() радианам, а
радианам, а ![]() соответствует
соответствует ![]() радиан.
радиан.
При переходе от радианной меры к градусной и наоборот проще всего использовать это соотношение:![]() .
.
Выразить радианы в градусы несложно, достаточно вместо![]() подставить
подставить ![]() и вычислить. Например:
и вычислить. Например:
.
В случае, когда надо перейти от градусной меры в радианную можно применять формулу: ![]() Но формулы имеют свойство забываться,
поэтому я предлагаю вам при необходимости составлять пропорцию.. Например, выразим 30
Но формулы имеют свойство забываться,
поэтому я предлагаю вам при необходимости составлять пропорцию.. Например, выразим 30![]() в радианах:
в радианах:
Наиболее часто употребляемыми углами являются углы в ![]() . Давайте переведем их в радианы и запишем на нашей окружности. Углы в
. Давайте переведем их в радианы и запишем на нашей окружности. Углы в
![]() находятся в первой четверти и составляют от него третью часть, половину и две третьих.
находятся в первой четверти и составляют от него третью часть, половину и две третьих.
Так как значение ![]() , значит
, значит ![]() , значит
, значит ![]() , следовательно, на окружности точка 1 расположена выше
, следовательно, на окружности точка 1 расположена выше ![]() . Значение
. Значение
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Значит, если мы хотим найти угол в 2 радиана, то видим, что он лежит между значениями 1,57 и 3,14, то есть во II четверти. Не забывайте, что угол мы отмечаем от положительного направления оси ОХ.
Соответственно угол в -1 радиан лежит в IV четверти. Также мы определяем, где лежит угол в ![]() , -
, -![]() . Для определения четверти для углов, равных
. Для определения четверти для углов, равных ![]() или
или ![]() мы должны определить, какая из них правильная дробь, а какая неправильная дробь. Правильную дробь
мы должны определить, какая из них правильная дробь, а какая неправильная дробь. Правильную дробь ![]() сравнить со значением
сравнить со значением ![]() и если она больше ее, то угол лежит во второй четверти (или наоборот), а
неправильную дробь
и если она больше ее, то угол лежит во второй четверти (или наоборот), а
неправильную дробь ![]() со значением
со значением ![]() и если она
меньше его, то угол лежит в третьей четверти. В итоге получаем, что
и если она
меньше его, то угол лежит в третьей четверти. В итоге получаем, что ![]() .
.
Мы, с вами рассматривая, новый материал при помощи единичной окружности выяснили, что ее еще называют тригонометрической, так как координатами точки на окружности являются функции синус, косинус, тангенс и котангенс. Определили, что синус и косинус могут принимать значения только от -1 до 1, а тангенс и котангенс от - бесконечности до + бесконечности. Рассмотрели координатные четверти, их границы, как найти в какой четверти лежит угол, разобрали, как связаны между собой радианы и градусы. При этом наша тригонометрическая окружность изменялась, обрастала все новыми значениями. Если бы мы продолжили работу по нахождению значений координат точки и углов, соответствующих координатам по нашей окружности, то она бы приняла вот такой вид. (Идет демонстрация слайда с единичной окружностью и говорится, что такие же окружности есть у вас на столах, для удобства в работе).
Разберем, как работать с этой окружностью. Нахождение значений угла или функции напоминает нахождение координаты точки по графику или определение положения точки по заданным координатам.
Например, найдем, чему будут равны:
При помощи круга мы можем находить значения углов не только до 360![]() , но и больших, так движение по кругу напоминает
движение по спирали: один оборот, второй оборот и так далее. Например, найдем, чему равны значения функций:
, но и больших, так движение по кругу напоминает
движение по спирали: один оборот, второй оборот и так далее. Например, найдем, чему равны значения функций: ![]()
Вы должны находить значение тригонометрических функций по известному значению одной из них. Например, найти чему будет равен косинус, тангенс или котангенс какого-то угла, если синус этого же угла принимает такое-то значение. Для этого надо знать формулы, которые связывают известную и неизвестную величины. В тригонометрии их называют тригонометрические тождества.
Вот основные из них: это основное тригонометрическое тождество, мы его с вами вывели ранее![]() вместе с вот этим
формулами:
вместе с вот этим
формулами: ![]() . А вот эти три тождества вытекают из предыдущих:
. А вот эти три тождества вытекают из предыдущих:
V. Первичное закрепление материала. (10 мин.)
Мы рассмотрели тригонометрические функции, но еще Жан Жак Руссо говорил, что час работы научит больше, чем день объяснения. Значит, пора переходить к решению упражнений. Но перед этим давайте еще раз коротко обговорим, какие новые знания мы сегодня получили и должны запомнить. Проведем блиц опрос по рассмотренному материалу.
Устная работа (повторение теории). Вопросы для учащихся.
- Какие тригонометрические функции мы рассматривали?
- Как определяют функцию синус, косинус, тангенс, котангенс?
- На какой оси находятся значения синуса, косинуса, тангенса котангенса?
- В каких пределах может изменяться значение синуса, косинуса, тангенса и котангенса?
- В какой четверти косинус больше 0, синус отрицателен, тангенс положителен, а котангенс меньше нуля?
- Что необходимо знать, чтобы определить знак функции?
- Какое направление считается положительным, а какое отрицательным?
- В каких единицах может выражаться угол?
- Как выполнить переход от радианной меры к градусной и наоборот?
Устная работа (решение упражнений). Задания для устной работы.
- Верно ли равенство:
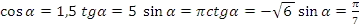 ?
? - Определите знак функции:
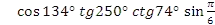 ?
? - Переведите радианную меру угла в градусную:
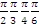 .
. - Найдите при помощи круга значение функций, объясните ответ:
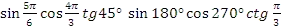 .
. - Найдите при помощи круга значение синуса, косинуса, тангенса, если величина угла равна:
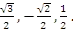
После окончания устной работы, отметить активных учащихся, поставить оценки за первый урок.
VI. Решение упражнений, работа по учебнику. (25 мин.)
Работа по решению упражнений идет у доски с вызовом учащихся и на местах. Каждое задание при наличии времени желательно разобрать перед решением.
1 задание: №3 ( а и в) из учебника «Алгебра 10-11» Колмогорова.
а)
б)
.
2 задание: текст задания дан на слайде презентации: найдите знак произведения:
а)
б)
в)
г)
3 задание: № 7 (а) по учебнику.
Найдите: ![]() ,
, ![]() ,
, ![]() .
.
Решение.
Так угол лежит в 3 четверти, то
Ответ: 0,6 ;![]() ;
; ![]() .
.
VII. Самостоятельная работа. (15 мин.)
Выполняется на листах через копирку. После решения работа первый раз проверяется учащимися в виде взаимопроверки, выставляются следующие оценки: за 3 задания -«3», за 4 задания - «4», за все 5 заданий оценка 5.
Задания для самостоятельной работы.
I вариант.
- Выразите в градусной мере величину угла:
 .
. - Выразите величину угла в радианах:
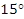 .
. - Найдите знак произведения, используя правило знаков по четвертям:
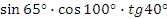 .
. - Вычислите значение выражения:
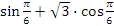 .
. - Найдите значение функции
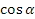 , если
, если 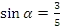 и
и
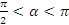 .
.
II вариант.
- Выразите в градусной мере величину угла:
 .
. - Выразите величину угла в радианах:
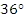 .
. - Найдите знак произведения, используя правило знаков по четвертям:
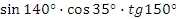 .
. - Вычислите значение выражения:
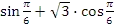 .
. - Найдите значение функции
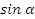 , если
, если 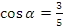 и
и
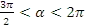 .
.
VIII. Разбор домашнего задания. (2 мин.)
Задание на дом вывести на слайд презентации: по учебнику № 31 (а и в), № 15 (г), № 3 (в и г).
IX. Рефлексия. (3 мин.)
Подвести итоги урока, проведя беседу с учащимися по вопросам: что узнали, что решали?