Цель занятия:
- Учебная повторение темы “Производная”, систематизация знаний по теме “Наибольшие и наименьшие значения функции”, применении е этих знаний в будущей профессии, решая задачи практического характера, приобщение творческой деятельности.
- Воспитательная воспитать интерес к математике и ее приложениям, расширение и углубление представлений об истории математики, о ее роли в мировой науке.
- Развивающая развитие логического мышления, памяти, формирование умений анализа и синтеза полученных знаний, развитие абстрактного мышления, научить выделять главное, развивать математический кругозор, развитие навыков работы с математической литературой.
Межпредметные связи:
- обеспечиваемые: связь с будущей профессией
- обеспечивающие: история, физика, экономика, литература, естествознание
ОБЕСПЕЧЕНИЕ ЗАНЯТИЯ
А. Наглядные пособия Презентация к уроку, учебные пособия, иллюстрации на интерактивной доске.
Б. Технические средства обучения компьютер, интерактивная доска.
В. Раздаточный материал учебник.
Г. Учебные места кабинет математики.
Д. Литература:
Основная
- А.Н.Колмогоров Алгебра и начала анализа. М., 2010
- Н.Ш.Кремер Высшая математика для экономистов. М., 2004
- Н.В.Богомолов Практические задачи по математике. М., 2007
Дополнительная
- З.С.Беляева, В.М.Мохов Экстремальные задачи. М., 2007
- П.И.Алтынов Тесты “Алгебра и начала анализа”. М., 2000
- Н.Я.Веленкин Задачник по курсу математического анализа. М., 2001
- Б.В. Гнеденко Энциклопедический словарь. М., “Педагогика”, 1989
СОДЕРЖАНИЕ ЗАНЯТИЯ
- Организационный момент
- Устный счет.
- Выступление студента “Из истории развития экстремальных величин”
- Нахождение наибольших и наименьших значений функции на отрезке
- Алгоритм отыскания наибольшего и наименьшего значения функции на отрезке
- Нахождение наибольших и наименьших значений функции на незамкнутом промежутке
- Самостоятельная работа на нахождение максимальных значений функции (взаимная проверка)
- Практические задачи на нахождение наибольших и наименьших величин
- Домашнее задание
- Подведение итогов
ХОД УРОКА
Вступительное слово.
СЛАЙД 1.
Ребята, в жизни человека всегда есть минуты, когда ему нужно быстро сосредоточиться, чтобы выполнить какое-либо дело. Для этого надо быть очень внимательным и находчивым, точным в расчетах. Об этом хорошо сказано в стихотворении В.Л. Лившица "Три десятых". Я зачитаю всего лишь четверостишие.
Три десятых - и стены возводятся косо!
Три десятых - рухнут вагоны с откоса!
Ошибись только на три десятых аптека –
Станет ядом лекарство, убьет человека...
I. Устный счет.
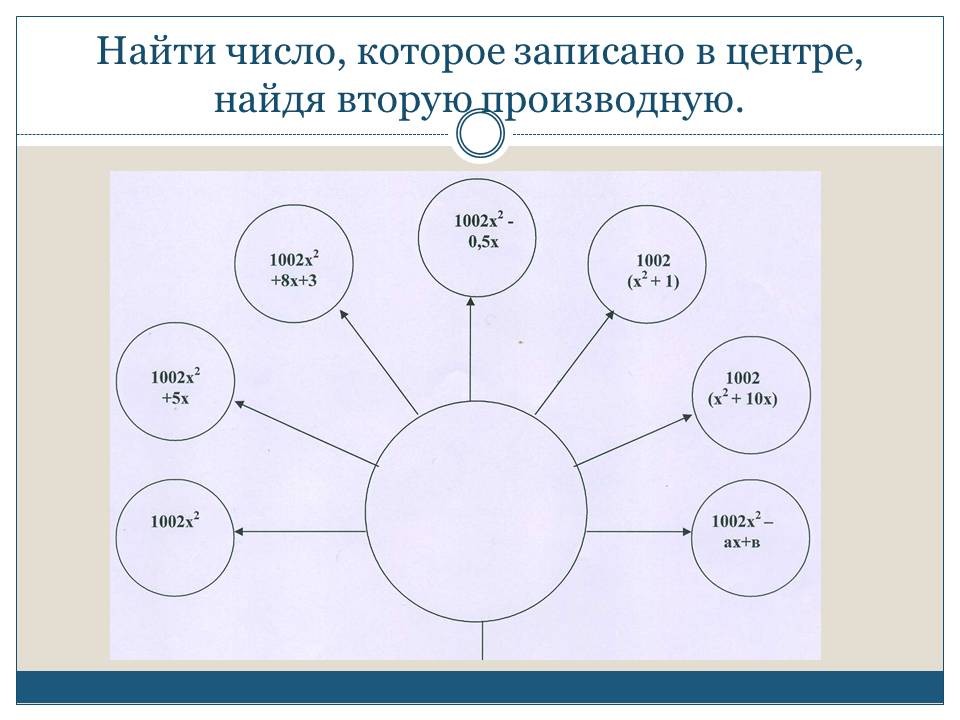
СЛАЙД 2. Сейчас мы проверим, как вы точны в математике, как усвоили тему “Производная”. Устно найдите вторые производные по данному чертежу.
II. Выступление студентов.
III. ИЗ ИСТОРИИ РАЗВИТИЯ ТЕОРИИ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИЙ ВЕЛИЧИН
СЛАЙД 3.
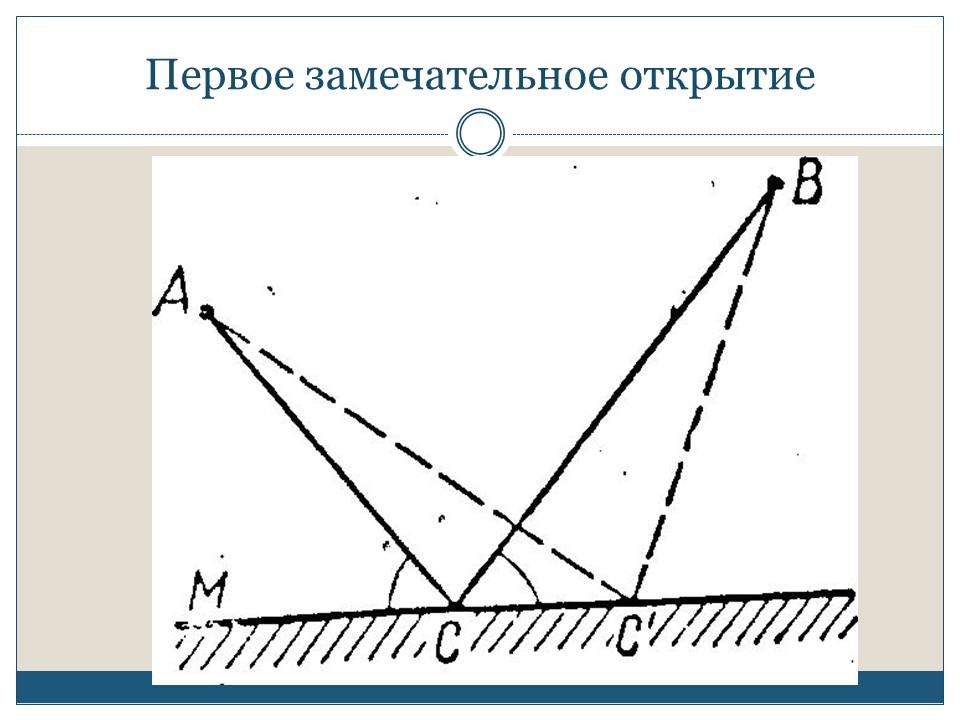
Первое замечательное открытие в области теории экстремальных значений величин относят к первому столетию нашей эры. Александрийский ученый Герои установил, что путь светового луча от точки А до точки В при отражении от зеркала в точке С является кратчайшим (минимальным) расстоянием от А до В с заходом на плоскость зеркала М. То, что световой луч, отражаясь от зеркала, образует с зеркальной поверхностью равные углы (угол падения светового луча равен углу отражения), было известно и раннее, но тот факт, что расстояние | АС | + | СВ | меньше | АC'| + | С'В |, где С' - любая другая точка зеркальной плоскости, отличная от С, т.е. расстояние | АС | + | СВ | является наименьшим, - это было открытием.
IV. Нахождение наибольших и наименьших значений непрерывной функции на отрезке.
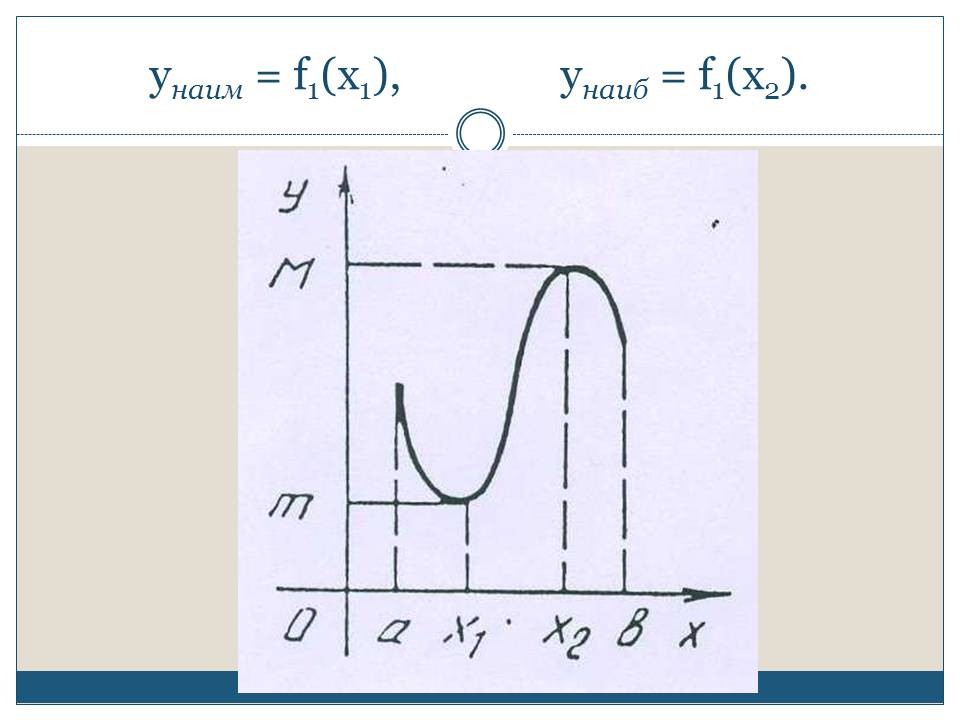
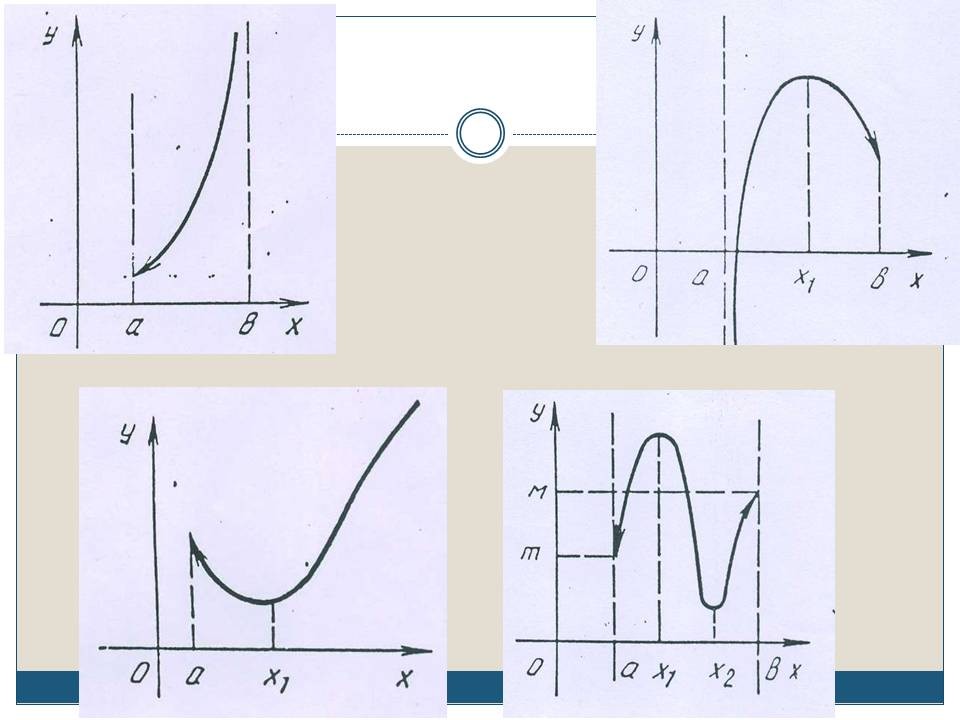
СЛАЙД4. Функция у = f1(х) непрерывна на отрезке [а, b], она достигает своих наименьшего и наибольшего значений во внутренних точках х1 и х2:
![]() = f1(х1),
= f1(х1),
![]() = f1(х2).
= f1(х2).
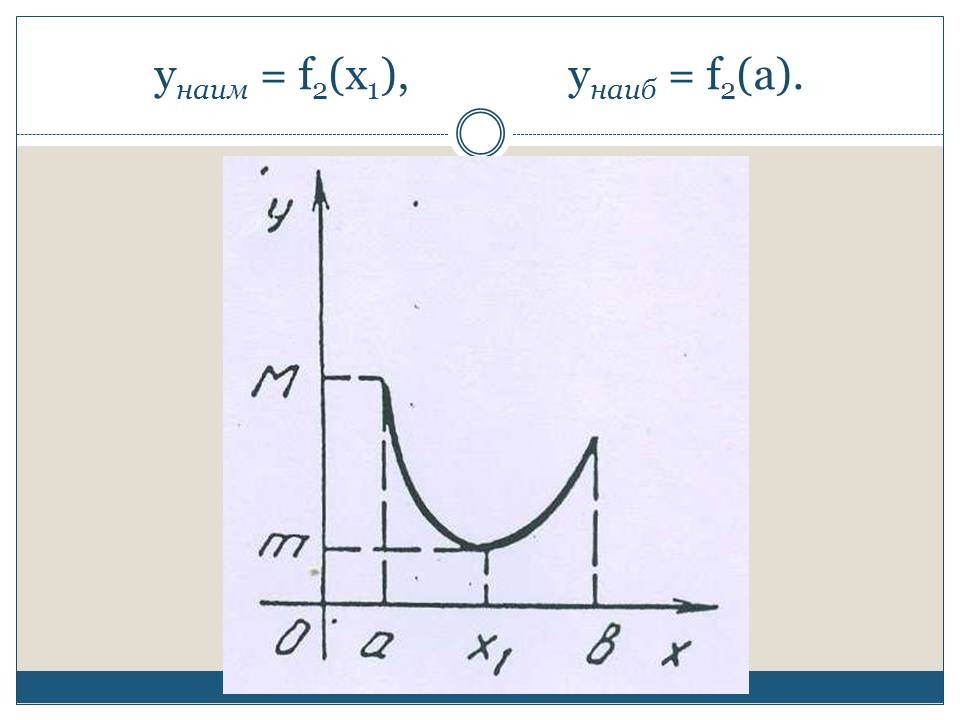
СЛАЙД 5. Функция у = f2(х) непрерывна на отрезке [а, b], она достигает своего наименьшего значения во внутренней точке х1, а своего наибольшего значения - в одном из концов отрезка (в данном случае в точке а):
![]() = f2(х1),
= f2(х1),
![]() = f2(а).
= f2(а).
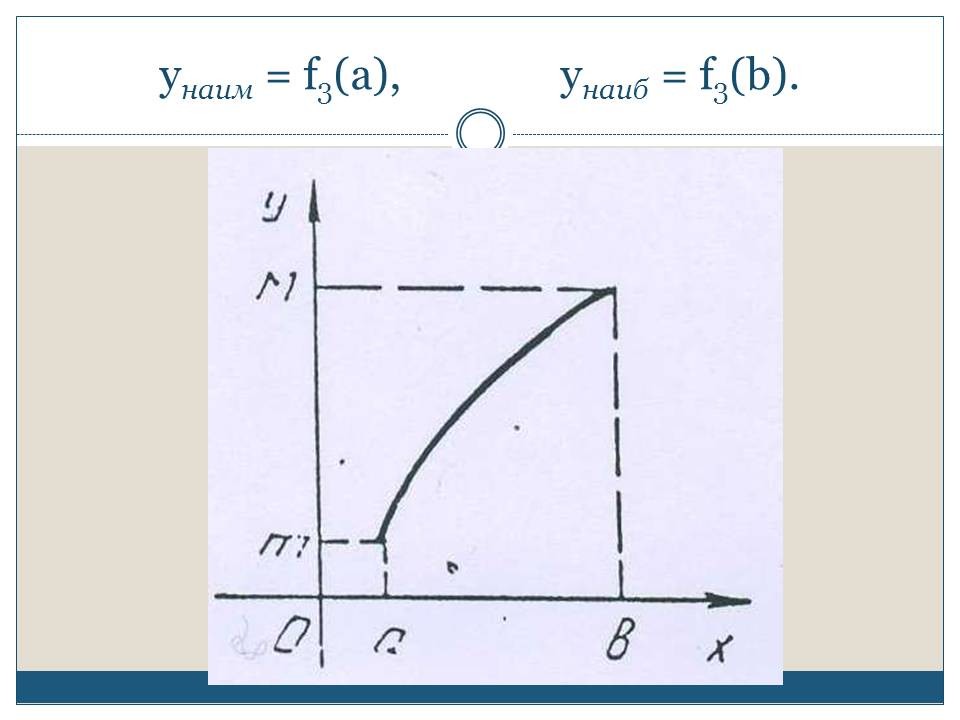
СЛАЙД 6. Функция у = f3(х) непрерывна на отрезке [а, b], она достигает своих наименьшего и наибольшего значений в концевых точках а и b:
![]() = f3(а),
= f3(а), ![]() = f3(b).
= f3(b).
Справедливы следующие теоремы - они даются без доказательства, но их справедливость наглядно иллюстрируется рассмотренными графиками.
Теорема 1. Функция, непрерывная на отрезке, достигает на нем своего наибольшего и своего наименьшего значения.
Теорема 2. Область значений функции у = f(х),
непрерывной на отрезке [а, b], представляет собой
отрезок [![]() ,
, ![]() ]
]
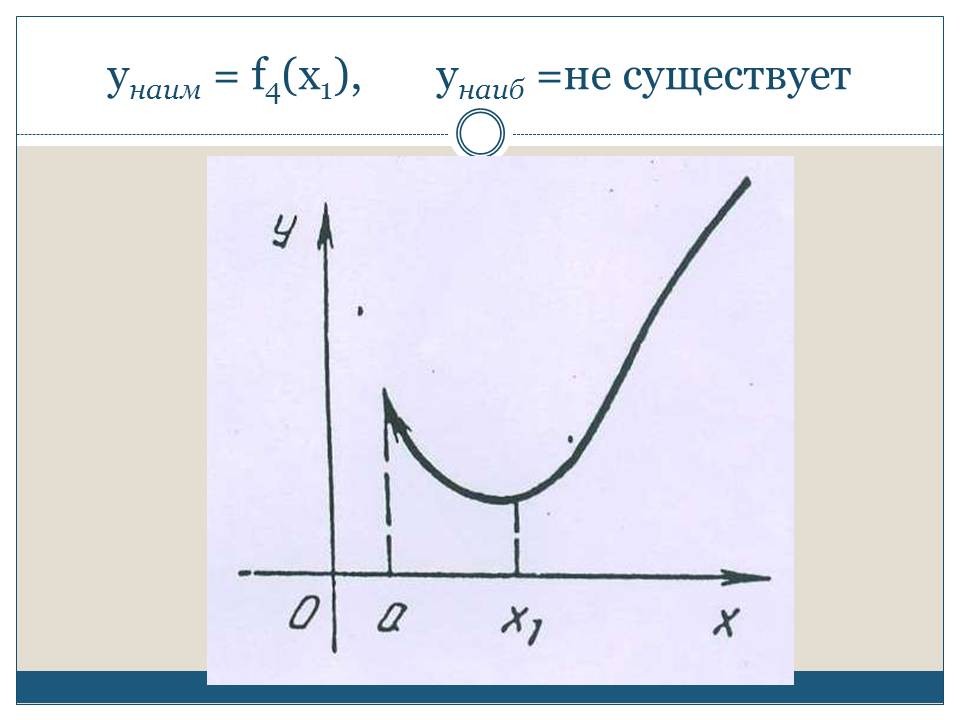
СЛАЙД 7. Функция у = f4(х) непрерывна на
незамкнутом промежутке (а, +![]() ), она на этом промежутке
достигает наименьшего значения во внутренней
точке х1, но не достигает своего
наибольшего значения (иными словами, на (а, +
), она на этом промежутке
достигает наименьшего значения во внутренней
точке х1, но не достигает своего
наибольшего значения (иными словами, на (а, +![]() ) нельзя найти точку с такую,
чтобы выполнялось неравенство f4(с)
) нельзя найти точку с такую,
чтобы выполнялось неравенство f4(с) ![]() f4 (х) для любого х из (а,
+
f4 (х) для любого х из (а,
+![]() ). Итак,
). Итак, ![]() = f4(х1),
= f4(х1), ![]() не существует.
не существует.
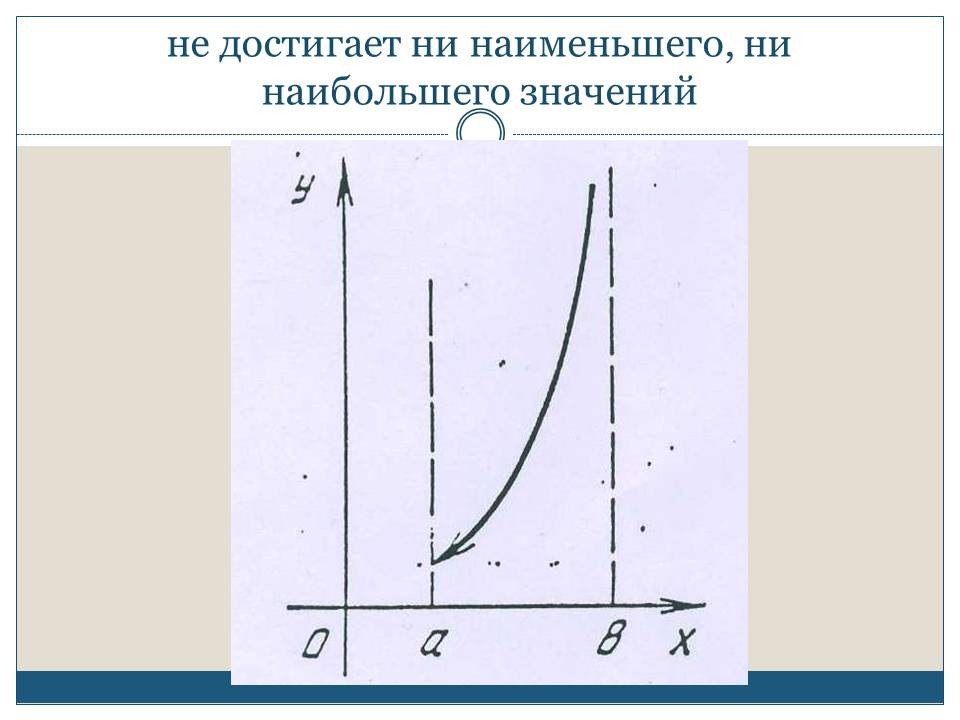
СЛАЙД 8. Наконец, функция у = f5 (х)
непрерывна на интервале (а, b) ( но не на отрезке [а,
b]), причем на этом интервале она не достигает ни
наименьшего, ни наибольшего значений (казалось
бы, что ![]() = f5(а),
но это не так, ибо в точке а функция не определена,
а потому о значении f5 (а) нет смысла
говорить, его нет).
= f5(а),
но это не так, ибо в точке а функция не определена,
а потому о значении f5 (а) нет смысла
говорить, его нет).
Два последних примера показывают, что у непрерывкой функции на незамкнутом промежутке может быть, а может и не быть наименьшего или наибольшего значения, но это не противоречит теореме 1. Это лишь заставляет нас очень внимательно относиться к каждому условию теоремы, не перенося ее автоматически на те случаи, для которых она не приспособлена: теорема 1 утверждает, что у функции, непрерывной на отрезке (т.е. на замкнутом промежутке), обязательно есть на этом отрезке и наибольшее, и наименьшее значения; про функцию же, непрерывную на незамкнутом промежутке, в теореме не говориться ровным счетом ничего. Ничего не говорит теорема и о функциях, не являющихся непрерывными.
СЛАЙД 9. Вернемся к функции у = f(х), непрерывной на отрезке [а, b]. Наибольшее и наименьшее значения функции существуют, но как их найти? Внимательное изучение рисунков позволяет нам заметить, что во всех случаях унаиб., унаим. достигались либо в концевых точках отрезка [а, b], либо в точках экстремума, расположенных в интервале (а, b). Поэтому достаточно вычислить значения функции в концевых точках отрезка и во всех внутренних точках экстремума и из этих значений выбрать наибольшее и наименьшее. Таким образом, мы получаем следующий алгоритм.
СЛАЙД 10.
V. Алгоритм отыскания наибольшего и наименьшего значений функции у=f(х), непрерывной на отрезке [а, b]
1. Найти f ' (х).
2. Найти точки, в которых f ' (х) не существует, и точки, в которых f '(х)=0; отобрать из них те, которые лежат внутри [а, b].
3. Вычислить значения функции у=f(х) в точках а, b и в точках, выделенных на шаге 2, и выбрать среди этих значений наибольшее (это будет унаиб) и наименьшее (это будет унаим).
Пример 1. Найти наибольшее и наименьшее значения функции у=х3-3х2-45х +225 на отрезке [0; 6].
Решение. Заданная функция непрерывна на заданном отрезке (и даже на всей числовой прямой), поэтому можно воспользоваться алгоритмом.
f,(х)=3x2-6x-45.
Производная существует при всех х. Найти точки в которых f,(х)=0: Зх3-6х-45=0 —> Х1=-3, х2=5. Отрезку [0; 6] принадлежит лишь точка Х2=5.
Вычислим значения функции в точках 0; 5; 6.
X 0 5 6 У 225 50 63
Наибольшим из найденных значений является число 225, наименьшим - число 50. Итак, унаиб = 225, унаим = 50.
Пример 2. Найти наибольшее и наименьшее значение функции у=5х3-х |х-1| на отрезке [0; 2].
Решение. Заданная функция непрерывна на всей числовой прямой, и, в частности, на заданном отрезке, поэтому можно воспользоваться предложенным выше алгоритмом.
Если х ![]() 1, то у=5х3-х(х-1)=5х3-х2+х;
если х
1, то у=5х3-х(х-1)=5х3-х2+х;
если х ![]() 1, то у=5х3+х(х-1)=5х3+х2-х.
Значит,
1, то у=5х3+х(х-1)=5х3+х2-х.
Значит,
f(х)=5х3+х2-х, 0
х
1,
f(х)=5х3-х2+х, 1
х
2.
Вычисляя f,(х), мы должны учесть, что при 0<х<1 надо пользоваться формулой 5х3+х2-х, а при 1<х<2 - формулой 5х3-х2+х; точка "стыка" х=1 - критическая точка (в ней производная не существует). Значит,
f(х)= 15х2+2х-1, если 0<х<1,
f(х)= 15х2-2х+1, если 1<х<2.
Производная, как мы отметили выше, не существует в точке х=1. Найдем точки, в которых f,(х)=0.
Если 0<х<1, то уравнение f,(х)=0 принимает вид: 15х2+2х-1=0, откуда находим х1=1/5, х2=-1/3. Из этих двух значений интервалу (0; 1) принадлежит лишь 1/5.
Если 1<х<2, то уравнение f,(х)=0 принимает вид: 15х2-2х+1=0 - это уравнение не имеет действительных корней. Итак, мы нашли две критические точки: 1/5, 1.
Вычислим значения функции в найденных точках и на концах отрезка.
X 0 1/5 1 2 У 0 -3/25 5 38
Из имеющихся в таблице значений наименьшим является -3/25, наибольшим 38.
Ответ: унаим =-3/25, унаиб =38.
VI. Нахождение наибольшего и наименьшего значений непрерывной функции на незамкнутом промежутке.
СЛАЙД 11. Мы уже отметили, что для функции, непрерывной на незамкнутом промежутке, ситуация является неопределенной: может быть так, что у функции нет ни наибольшего, ни наименьшего значений; есть наименьшее, но нет наибольшего значения; есть наибольшее, но нет наименьшего значения; есть и наибольшее и наименьшее значения.
Поскольку на концах промежутка функция не определена, то ясно, что унаиб, унаим (если они, конечно, есть) достигаются функцией во внутренних точках промежутка, причем, как мы отмечали в пункте 3, только в критических точках. Значит, как и в случае непрерывной функции на отрезке, нам надо сначала найти f,(х), затем выделить те критические точки функции f(х), которые лежат внутри заданного промежутка, затем вычислить значения функции f(х) в выделенных точках, то есть на первый взгляд кажется, что можно придерживаться того же алгоритма.
И тут возникает серьезная проблема: дело в том, что полученные значения функции нам по существу ничего не говорят.
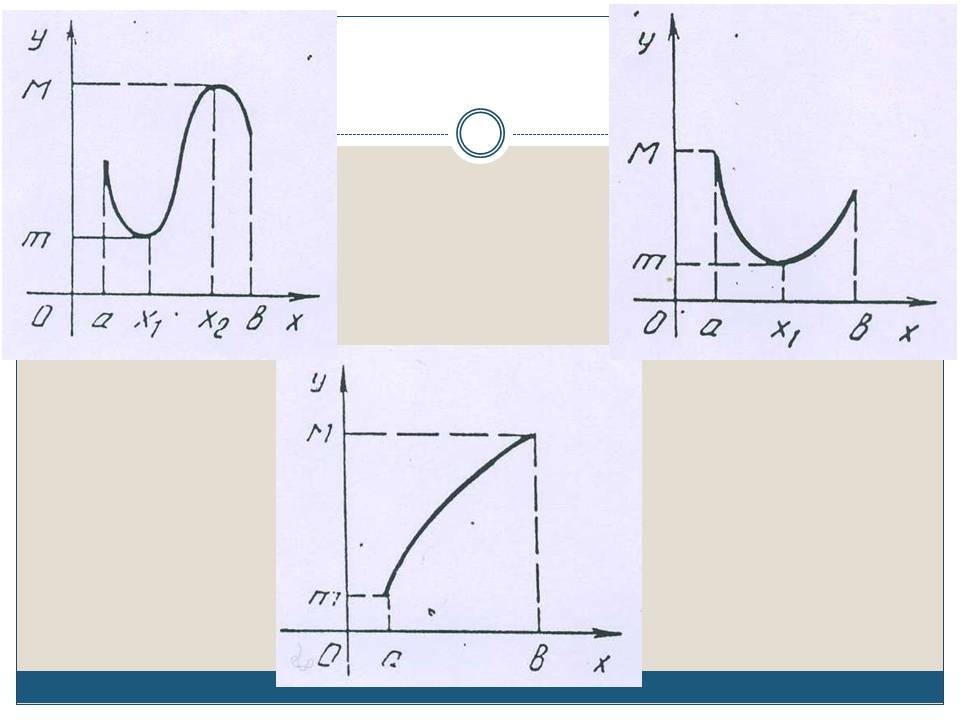
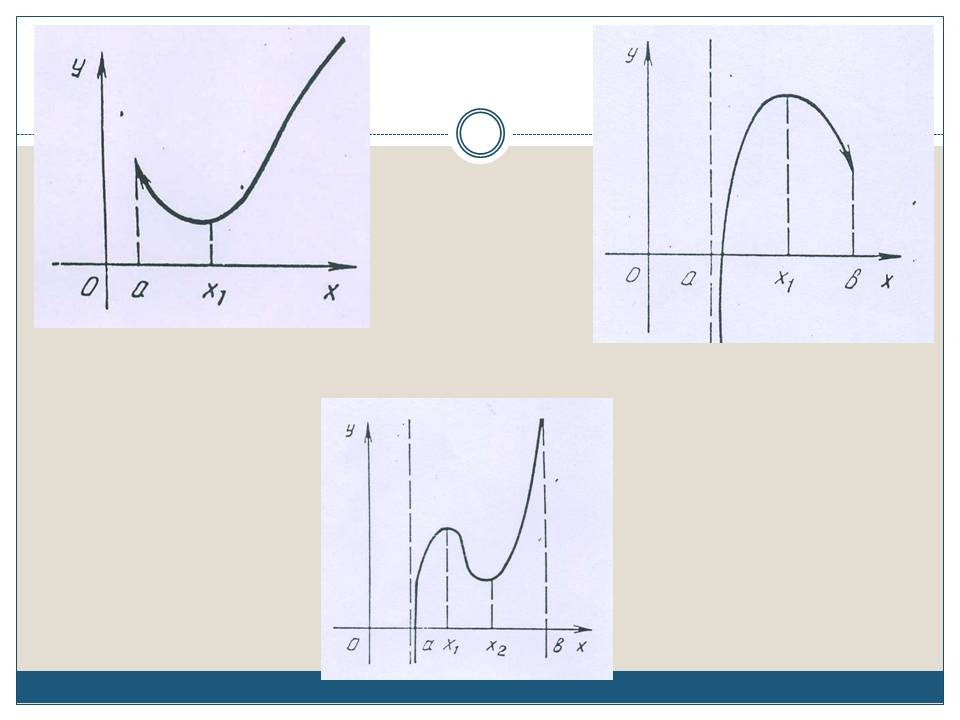
СЛАЙД 12. Смотрите сами: на первом графике критическая точка одна - это точка х1 при этом f(х1)= унаим; на втором графике критическая точка одна - это точка x1 при этом f(х1)= унаиб; на третьем графике критических точек две - это точки x1 и х2, при этом ни наибольшего, ни наименьшего значений у функции нет.
Как же быть? На наше счастье, наиболее часто встречается на практике случай, когда внутри заданного промежутка заданная непрерывная функция имеет только одну точку экстремума. Тогда нас выручит следующая теорема.
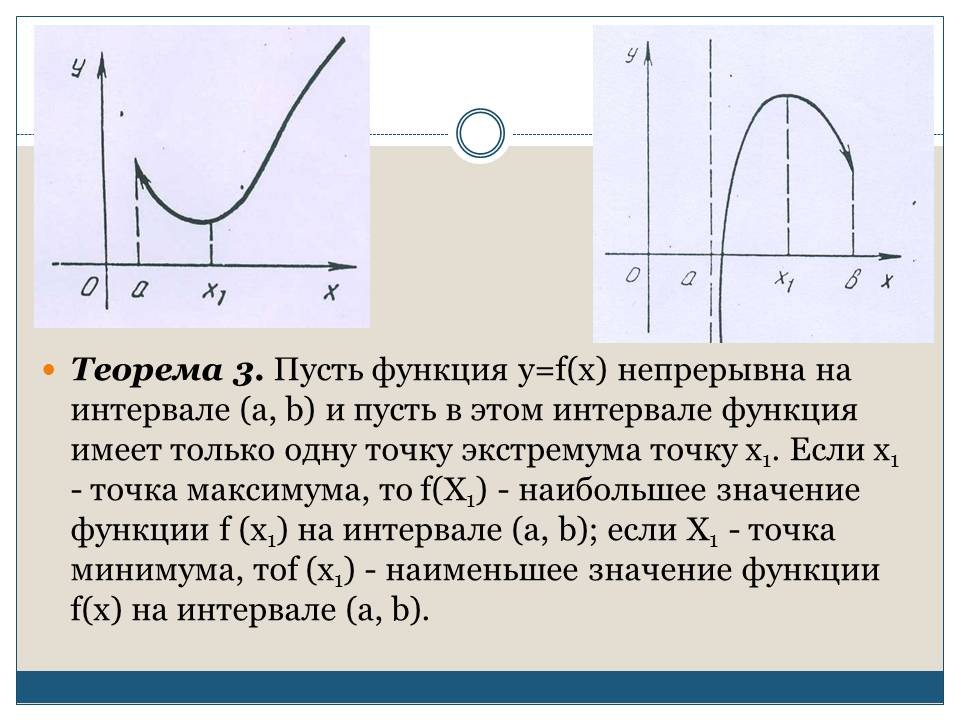
СЛАЙД 13. Теорема 3. Пусть функция у = f(х) непрерывна на интервале (а, b) и пусть в этом интервале функция имеет только одну точку экстремума точку x1. Если х1 - точка максимума, то f(X1) - наибольшее значение функции f (х1) на интервале (а, b); если X1 - точка минимума, то f (х1) - наименьшее значение функции f(х) на интервале (а, b).
Эту теорему отчетливо иллюстрируют ситуации, изображенные на графиках.
Между прочим, теорема справедлива и для отрезка
[а, b]. Однако применяя теорему 3 к интервалу (а, b), к
отрезку [а, b] или к полуинтервалу [а, b), вы должны
учитывать следующие обстоятельство: пусть x1
![]() (а, b) и x1
- точка максимума функции у=f(х), непрерывной на
промежутке с концами а и b (напоминаем, что х1
- единственная точка экстремума функции на
заданном промежутке).
(а, b) и x1
- точка максимума функции у=f(х), непрерывной на
промежутке с концами а и b (напоминаем, что х1
- единственная точка экстремума функции на
заданном промежутке).
СЛАЙД 14. Тогда f(х1) = унаиб. Что же касается унаим, то:
- в случае (а, b) унаим не существует;
- в случае [а, b] унаим существует - это будет либо f(а), либо f(b);
- в случае [а, b) унаим может существовать (и тогда это будет f(а)), а может и не существовать (смотрим график на слайде).
Пример 3. Найти наименьшее и наибольшее (если они есть) значения функции у=х3 -9х2 +15х на интервале (0; 8).
Решение.
Имеем f,(х)=Зх2-18х+15.
f,(х) существует при любых x; найдем точки, в которых f'(х)=0. Имеем 3x2-18x+15=0, откуда х1=1, х2=5. Обе точки принадлежат заданному интервалу.
f(1)=1-9+15=7; f(5)=125-225+75=-25;
![]() f(x) =
f(x) = ![]() (х3-9х2+
15х)=0;
(х3-9х2+
15х)=0;
![]() f(x) =
f(x) =![]() (х3-9х2+15х)=512-576+120=56.
(х3-9х2+15х)=512-576+120=56.
Рекомендуем использовать следующую запись:
x —> 0 —> 8 1 5 у —> 0 —> 56 7 -25
Сравнивая значения в критических точках (7 и -25) с пределами функции на концах промежутка (0 и 56), делаем вывод: унаим = -25, унаиб не существует.
Ответ: унаим = -25.
VII. Самостоятельная работа
СЛАЙД 15.
Вариант I
- Найдите наибольшее значение функции f(х)=х3-2х2+х-3 на промежутке [1/2; 2]. а) 1/9; б) 1; в) -1; г)-2,852.
Вариант II
- Найдите наибольшее значение функции f (x) =х3+3x2-9х-1 на промежутке [-4; -1/3].
а) 26; б) 19; в) 30 г) 15.666.
VIII. Задачи на экстремум.
СЛАЙД 16. Задачи, где требуется определить условия, при которых некоторая величина принимает наибольшее и наименьшее значение, принято называть задачами “на экстремум” (от латинского слова extremum - “крайний”) или задачами “на максимум и минимум” (от латинских maximum и minimum - соответственно “наибольшее” и “наименьшее”). Такие задачи часто встречаются в технике и естествознании, в повседневной жизни людей.
Как из круглого бревна выпилить прямоугольную балку с наименьшим количеством отходов? Каких размеров должен быть ящик, чтобы при заданном расходе материала его объем был наибольший? В каком месте следует построить мост через реку, чтобы дорога, проходящая через него и соединяющая два города, была кратчайшей?
Эти задачи имеют большое практическое значение. С их помощью можно решить важный во всяком деле вопрос, как, по словам русского математика П.Л. Чебышева, “располагать средствами своими для постижения по возможности большей выгоды”. Уметь решать подобные задачи очень важно, и поэтому они привлекают большое внимание математиков.
Примерный план решения тестовых задач на экстремум таков:
- Выбрать независимое переменное и установить область его изменения.
- Выразить исследуемую величину через аргумент.
- Найти стационарные точки и точки, в которых исследуемая функция не имеет производной (в частности, точки, где производная обращается в бесконечность). Из числа последних точек исключить точки несуществования функции.
- Вычислить значения функции в найденных точках и на концах отрезка изменения аргумента и выбрать из этих значений наибольшее и наименьшее.
Пример 1. В степи на расстоянии 9 км к северу от шоссе, идущего с запада на восток, находится поисковая партия. В 15 км к востоку от точки на шоссе, ближайший к поисковой партии, расположен райцентр. Поисковая партия отправляет курьера-велосипедиста в райцентр. Каким должен быть маршрут следования курьера, чтобы он прибыл в райцентр в кратчайший срок, если известно, что по степи он едет со скоростью 8 км/ч, а по шоссе - со скоростью 10 км/ч?
Пример 2. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеется а погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?
Пример 3. Капитал в 1млрд. рублей может быть размещен в банке под 50% годовых или инвестирован в производство, причем эффективность вложения ожидается в размере 100%, а издержки задаются квадратичной зависимостью. Прибыль облагается налогом в р%. При каких значениях р вложение в производство является более эффективным, нежели чистое размещение капитала в банке?
Пример 4. Завод А расположен в стороне от железной дороги так, что кратчайшее расстояние от завода до дороги составляет 15 км. Продукция завода должна поставляться в город В, через который проходит указанная железная дорога. Кратчайшее расстояние от завода до города составляет 150 км. Рассмотренный участок является прямым. Стоимость перевозки тонны груза на расстояние 1 км по автотрассе в 4 раза превышает стоимость аналогичных перевозок по ж/д. Дирекция завода решила построить подъездной путь под некоторым углом а к железной дороге. Каким следует выбрать этот угол, чтобы сделать транспортировку грузов из А в В наиболее экономичной?
IX. Заключение.
При решении задач практического содержания часто можно не проверять аналитически достаточность условий экстремума (с помощью первой или второй производной). Заключение о наличии обычно легко сделать на основании условий задачи. Но желательно придерживаться плана рассмотренного выше.
СЛАЙД 17. Задание на дом: решить пример 3, 4.; из учебника “Высшая математика для экономистов” Н.Ш.Кремер изучить теоретический материал главы 8 п.8.3–8.5.
Подведение итогов.