Тема урока: "Решение показательных неравенств"

Проблема:

На уроке будут рассмотрены новые для обучающихся неравенств – показательные, решение которых требует хорошего знания теоретического материала. Данные неравенства ежегодно присутствуют в вариантах ЕГЭ по математике.

Цели урока:

• обобщение знаний и умений учащихся по применению методов решения показательных уравнений;
• закрепление свойств показательной функции в процессе решения показательных неравенств;
• развитие умения систематизации изученного материала, выделения общих и отличительных признаков и свойств изучаемых понятий, умения применять функционально-графический метод при решении уравнений и неравенств;
• формирование заинтересованности учащихся в решении нестандартных показательных уравнений и неравенств при подготовке к ЕГЭ.

• активизация познавательной деятельности посредством использования компьютерных технологий;
• развитие навыков самоконтроля и самооценки, самоанализа своей деятельности.

• формирование умения работать самостоятельно, принимать решения и делать выводы;
• воспитание устремленности к самообразованию и самосовершенствованию;
• осознание учащимися социальной, практической и личной значимости учебного материала по изучаемой теме

Оборудование: компьютер, мультимедийное оборудование.

Урок построен таким образом, чтобы учащиеся, опираясь на свойства степени и свойства числовых неравенств, а также на свойство монотонности показательной функции, самостоятельно пришли к алгоритму решение показательных неравенств и применили его при решении простейших неравенств.

Теоретический опрос: а) определение показательной функции; б) какова область определения показательной функции; в) какова область значений показательной функции; г) в каком случае показательная функция является возрастающей, убывающей; д) как расположен график; е) каковы основные методы решения показательных уравнений (метод замены, однородное уравнение, разложение левой части уравнения на множители и переход к совокупности, функционально – графический, метод интервалов); ж) что называется решением неравенства, что значит решить неравенств.

Цель: Проверка домашнего задания.

Повторение приемов решения показательных уравнений используемых также при решении показательных неравенств.

На интерактивной доске заранее записаны решения уравнений из домашнего задания. Учащимся предлагается сверить свои решения с записями на доске и найти допущенные в решениях ошибки.

Ошибки допущены в уравнениях 2,3,4 и выделены полужирным шрифтом, а та часть решения, где содержится ошибка, подчеркнута.

Цель: Повторение свойства степени при работе с числовыми неравенствами.

На каждом столе находится карточка с заданиями. Учащиеся обсуждают в парах. Для выполнения этих заданий им необходимо вспомнить свойства степени:

Сравните числа (поставьте знаки “>”  или “<” вместо многоточия):

Сравните показатели “m” и “n”, если верны неравенства:

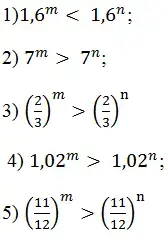
Задание 3.

Сравните с единицей основания , если известно, что:

IV. Фронтальная работа с классом.

Цель: Повторение свойство возрастания-убывания показательной функции и применение его при решении показательных неравенств.

Вопрос к классу: Какое свойство показательной функции было доказано ранее c помощью свойств степени, использованных в задания 1,2 и 3 ?

Ответ: Свойство монотонности.

Ученики формулируют данное свойство, опираясь на графическую иллюстрацию на доске.

Применяя свойство монотонности показательной функции

1) указать несколько значений x, которые следующие неравенства обращают в верные числовые неравенства

2) записать все решения следующих неравенств

Проанализировать результаты задания 4 и попытаться сформулировать правило решения простейших показательных неравенств вида

Далее на доске записывается тема урока: “Решение показательных неравенств”.

Правило, сформулированное учениками, переводится на математический язык и записывается на доске:

Цель: Применение алгоритма решения показательных неравенств при решении простейших показательных неравенств.

Решить неравенства:

Выполняя это задание, учащиеся обсуждают решение в парах, а затем решение комментируется одним из учеников, а ответы записываются на доске.

Цель: Решение более сложные показательных неравенств сведением их различными способами к простейшим, когда можно применить сформулированный на уроке алгоритм.

Рассмотрим методы решения показательных неравенств, не являющихся простейшими. При их решении используются приёмы преобразования выражений, стоящих в левой и правой частях неравенства, аналогичные тем, которые использовались и при решении показательных уравнений.

а) Метод замены переменной. В этом случае новая неизвестная подбирается так, чтобы относительно неё неравенство не было показательным.

б) Решение однородных неравенств. При решении однородных неравенств используется свойство показательной функции a^x > 0, производим деление обеих частей неравенства на положительную величину и вводим новую переменную. Однородное неравенство первой степени ma^x + nb^x > 0 решается делением обеих частей неравенства на a^x > 0, а однородное неравенство второй степени ma^2x + nb^2x + ka^xb^x > 0 решается делением на a^2x (или b^2x,  или a^xb^x).

Пример: 2^x+1 – 3∙10^x > 5^2x+1  

Решение:

Так как 5^2x> 0  для любых x, то разделив обе части неравенства на 5^2x, получим неравенство, равносильное данному:

Пример:

4^x < 3∙ +

Решение. Рассмотрим функцию f(x) =  4^x – 3∙ – , областью определения которой является множество неотрицательных чисел. Находим нули функции, решив уравнение

4^x – 3∙ – = 0. Делим обе части уравнения на , после преобразований получим уравнение ()² – 3∙ – 4 = 0 , откуда = 4 или = -1.  Последнее уравнение не имеет решения, а уравнение = 4  имеет единственный корень, равный 4. Нуль функции разбивает область определения на промежутки , в которых функция (в силу своей непрерывности) сохраняет знак.

f(1) < 0.

f(9) = 4⁹ – 3∙2¹² – 4⁴ = 4⁴∙(4⁵ – 48 – 1) > 0

Итак, исходное неравенство выполняется при 0 < x < 4. Ответ:

Пример: 2^x < 3 – x

Решение. Функции f(x) = 2^x и g(x) = 3  – x  и определены на всём множестве действительных чисел. Функция f(x) = 2^x возрастающая на R, а функция  убывающая на R, значит, уравнение f(x) = g(x) имеет не более одного корня. Не сложно убедиться в том, что 1 является единственным корнем уравнения. Таким образом, графики функций имеют одну точку пересечения. Неравенство имеет решение тогда, когда график функции f(x) = 2^x  лежит не выше графика функции

g(x) = 3 – x, то есть при x < 1.

Ответ:

Цель: Закрепление навыка решения показательных уравнений повышенной сложности и умения решать показательные неравенства.

Задание:

1) Решить уравнения:

2) Решить неравенства №№ 29 (3, 4), 30 (3, 4).