Метод интервалов – один из наиболее часто используемых методов решения неравенств с одной переменной.
В курсе алгебры и начал анализа рассматривается следующее свойство непрерывных функций:
Если на интервале (а; b) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак.
На этом свойстве непрерывных функций основан метод интервалов.
Пусть функция f непрерывна на промежутке X и обращается в нуль в конечном числе точек этого интервала. По сформулированному выше свойству этими точками промежуток Х разбивается на интервалы, в каждом из которых непрерывная функция f сохраняет постоянный знак.
Это утверждение можно проиллюстрировать следующим образом.
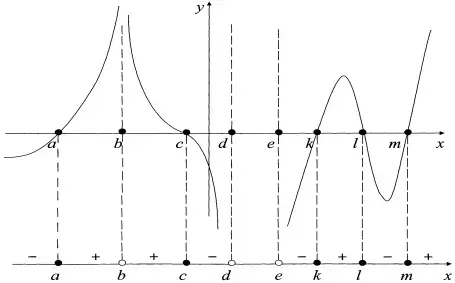
Пусть дан график некоторой функции 
. На числовой
прямой отметим область определения функции, нули
функции, точки разрыва, и тогда видно, что на
каждом из полученных промежутков области
определения функция имеет определенный знак.
Точки a, c, k, l, m изображают
нули функции, и если неравенство нестрогое (
), то точки закрашиваем и
эти значения переменной включаем в ответ. На
рисунке показано, что в точках b, d, e, а
также на интервале 
функция не существует, поэтому
указанные точки изображаются как “выколотые”.
Следует обратить внимание, что знаки на
промежутках не всегда чередуются.
Делаем вывод, что при решении неравенства методом интервалов в правой части неравенства нужно получить нуль (“+”, “–” – это сравнение значений функции с нулем, определение ее знака), а левая часть неравенства должна быть по возможности разложена на множители наименьшей степени.
Из вышесказанного можно составить алгоритм решения неравенств методом интервалов.
Пусть дано неравенство 
(
- Рассмотрим функцию
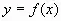
- Найдем область ее определения
- Найдем нули функции.
- На числовой прямой отметим область определения,
нули функции и точки разрыва функции, входящие в
область ее определения. Обозначим интервалы, на
которые отмеченные точки делят
- Методом “пробных точек” (или следуя известным алгоритмам) определим знак функции на каждом из полученных интервалов.
- Запишем ответ.
Учащимся можно сказать, что при решении несложных неравенств подробно этапы решения обычно не описывают, но при решении более сложных неравенств подробная запись этапов необходима, так как позволяет избежать многих ошибок.
Пример 1. Решить неравенства:
а)
б)
в)
Решение. Для приведенных выше неравенств подробная запись решения не обязательна. Покажем, например, решение последнего неравенства.
в) Неравенство
равносильно следующему неравенству:
Следует обратить внимание учащихся, что не всегда знак на крайнем правом промежутке будет “+”, а также на то, что знаки функции на промежутках не всегда чередуются. Можно доказать следующее утверждение: если каждый линейный множитель в левой части неравенства стоит в нечетной (в том числе и первой) степени, то знаки чередуются. Если же какой-то из множителей стоит в четной степени, то при переходе функции через точку, которая обращает в нуль этот множитель, знак функции изменяться не будет.
Пример 2. Решить неравенство 
.
Решение. Разложив квадратный трехчлен в
левой части неравенства на множители, получим: 
Заметим, что множитель 
находится в неравенстве в
четной степени, и поэтому при переходе через
точку 
знак
функции не изменился.
Может оказаться, что не все рациональные множители степени выше первой раскладываются на линейные множители, или встречаются множители, не являющиеся рациональными. Если некоторое выражение в нуль не обращается, то при всех допустимых значениях переменной оно будет либо положительным, либо отрицательным, то есть нужно выяснить, какой именно знак имеет этот множитель и затем учитывать его при определении знаков функции на промежутках.
Пример 3. Решить неравенство 
Решение. Рассмотрим квадратный трехчлен 
. Так как его
дискриминант отрицателен, а старший коэффициент
положителен, то данный квадратный трехчлен
принимает только отрицательные значения при
любых значениях переменной х. С учетом этого
результата решим данное неравенство методом
интервалов:
Ответ:
Пример 4. Решить неравенство 
Решение. Так как 
при всех 
R, то 
Кроме того, 
, поэтому 
, значит, значение выражения 
отрицательно
при любом 
R. Решая
неравенство методом интервалов с учетом знаков
выражений 
(“+”) и 
(“–”) получаем:
Ответ:
В более сложных случаях, чтобы избежать ошибок, желательно подробно записывать решение неравенства по тому алгоритму, который был рассмотрен выше.
Пример 5. Решить неравенство 
.
Решение:
1) Рассмотрим функцию 
2) Найдем 
Получаем: 
3) Найдём нули функции: 
откуда находим
и 
Заметим, что 
нулём функции не является, так как не входит в 
4) Отмечаем нули функции на её области определения и методом пробных точек на каждом из полученных промежутков определяем знак функции.
Ответ: 
Методом интервалов можно решать и более сложные неравенства, встречающиеся во второй части ЕГЭ.
Пример 6. Решить неравенство 
Решение:
1) Перепишем неравенство в следующем виде: 
Рассмотрим функцию
2) Найдем 
Решая последнее неравенство методом
интервалов, получаем: 
3) Найдем нули функции:
– нуль функции.
4) 
Точка 
входит в 
, но
нулем функции не является (функция в ней
положительна).
Ответ:
Пример 7. Решить неравенство 
Решение:
1) Рассмотрим функцию 
.
2) Найдем 
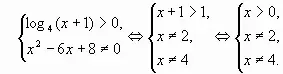
3) Найдем нули функции: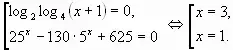 
Ответ: 
Можно применять метод интервалов и к решению неравенств с двумя переменными.
Пример 8. Изобразить на координатной плоскости множество решений неравенства
Решение. Разложив левую часть неравенства на множители, получим:
(1)
По аналогии с тем, как мы отмечали нули функции
на числовой прямой, построим в декартовой
системе координат линии 
и 
, которые разбивают координатную
плоскость на области. В каждой из полученных
областей берём “пробную” точку с координатами 
и, подставляя
ее координаты в неравенство (1), определяем его
истинность. Например, подставляя координаты
точки A(3;4), получим: 
–
верно.
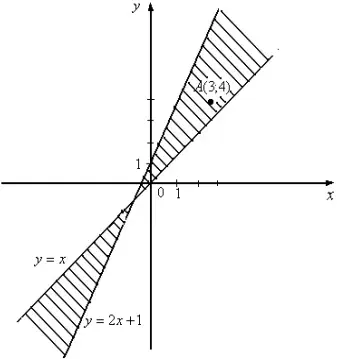
Подобно тому, как точки разбивают числовую
прямую на промежутки, на каждом из которых левая
часть неравенства сохраняет постоянным свой
знак, так и построенные линии разбивают
координатную плоскость на области, в каждой из
которых левая часть неравенства будет сохранять
свой знак. Закрасим эти части плоскости.
Множеством решений неравенства будут являться
все пары чисел 
, которые являются координатами точек
закрашенной части плоскости, включая точки
границы (так как неравенство строгое).
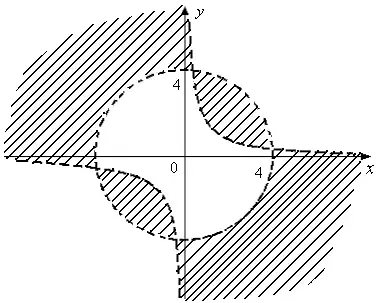
Пример 9. Изобразить на координатной плоскости множество решений неравенства
Решение. Построим графики уравнений 
и 
в одной системе координат.
Графиком первого уравнения является окружность
с центром в начале координат и радиусом 4,
графиком второго уравнения – гипербола 
Методом пробных точек определяем, что
множеством решений неравенства будут являться
все пары чисел 
, которые являются координатами точек
заштрихованной части плоскости, не включая точки
границы (так как заданное неравенство является
строгим.
