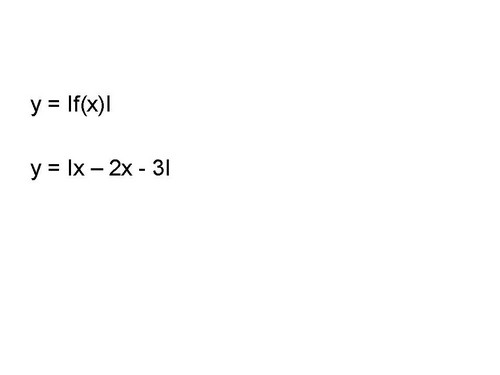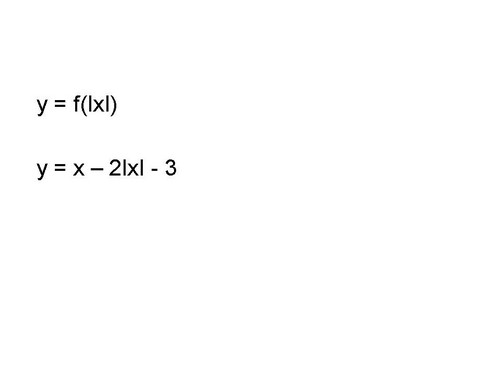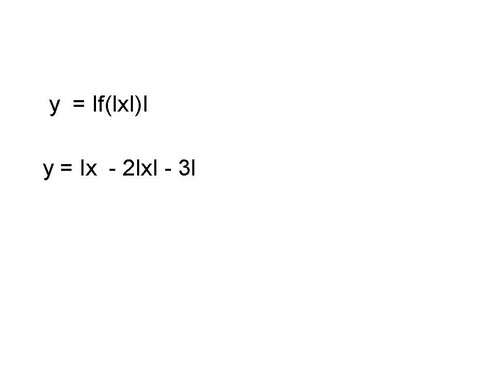Методы построения графиков функций содержащих модуль

Цель урока:

• повторить построение графиков функций содержащих знак модуля;
• познакомиться с новым методом построения графика линейно-кусочной функции;
• закрепить новый метод при решении задач.

Оборудование:

• мультимедиа проектор,
• плакаты.

Ход урока

Актуализация знаний

На экране слайд 1 из презентации.

Что является графиком функции y=|x| ? (слайд 2).

(совокупность биссектрис 1 и 2 координатных углов)

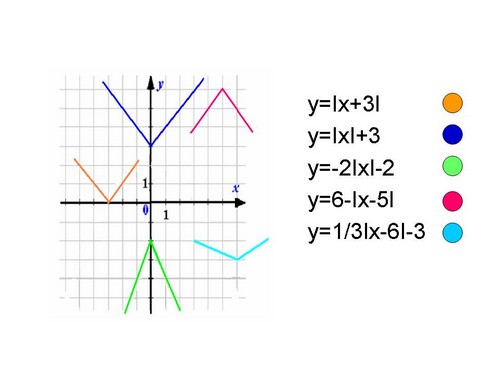
Найдите соответствие между функциями и графиками, объясните ваш выбор (слайд 3).

Рисунок 1

y=| x+3|

y=| x| +3

y=-2| x| -2

y=6-| x-5|

y=1/3| x-6| -3

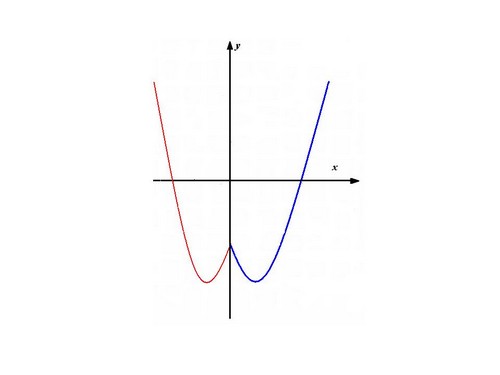
Расскажите алгоритм построения графиков функций вида y=|f(x)| на примере функции y=|x²-2x-3| (слайд 4)

Ученик: чтобы построить график данной функции нужно

- построить параболу y=x²-2x-3

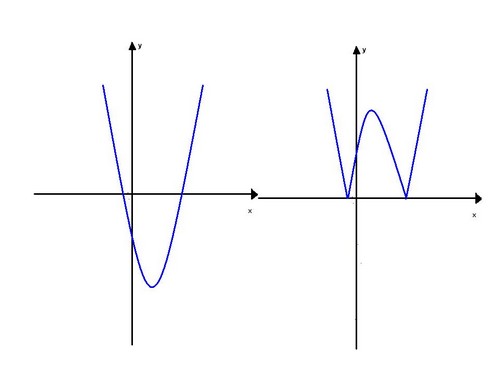
- часть графика над ОХ сохранить, а часть графика расположенную ниже ОХ отобразить симметрично относительно оси ОХ (слайд 5)

Рисунок 2

Рисунок 3

Расскажите алгоритм построения графиков функций вида y=f(|x|) на примере функции y=x²-2|x|-3 (слайд 6).

Ученик: Чтобы построить график данной функции нужно:

- построить параболу.

- часть графика при х 0 сохраняется и отображается симметрии относительно оси ОУ (слайд 7)

Рисунок 4

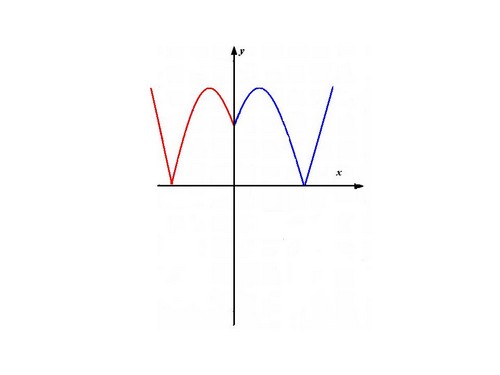
Расскажите алгоритм построения графиков функций вида y=|f(|x|)| на примере функции y=|x²-2|x|-3| (слайд 8).

Ученик: Чтобы построить график данной функции нужно:

- нужно построить параболу у=x²-2x-3

- строим у= x²-2|x|-3, часть графика сохраняем и симметрично отображаем относительно ОУ

- часть над ОХ сохраняем, а нижнюю часть симметрично отображаем относительно ОХ (слайд 9)

Рисунок 5

Следующее задание выполняем письменно в тетрадях.

1. Построить график линейно-кусочной функции у=|х+2|+|х-1|-|х-3|

Ученик на доске с комментарием:

- находим нули подмодульных выражений х₁=-2, х₂=1, х₃=3

- разбиваем ось на промежутки

- для каждого промежутка запишем функцию

при х < -2, у=-х-4

при -2 х<1, у=х

при 1 х<3, у = 3х-2

при х 3, у = х+4

- строим график линейно-кусочной функции.

Мы с вами построили график функции используя определение модуля (слайд 10).

Рисунок 6

Предлагаю вашему вниманию “метод вершин”, который позволяет строить график линейно-кусочной функции (слайд 11). Алгоритм построения дети записывают в тетрадь.

Метод вершин

Алгоритм:

1. Найдем нули каждого подмодульного выражения
2. Составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа
3. Нанесем точки на координатную плоскость и соединим последовательно

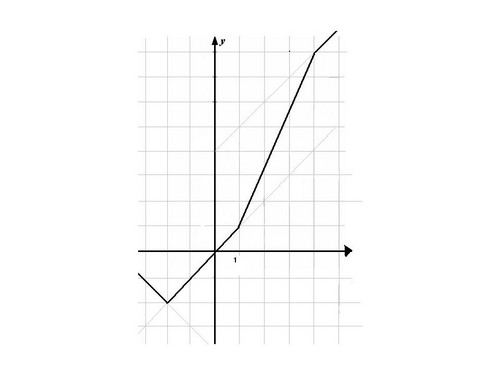
2. Разберем этот метод на той же функции у=|х+2|+|х-1|-|х-3|

Учитель на доске, дети в тетрадях.

Метод вершин:

- найдем нули каждого подмодульного выражения;

- составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа

х -3 -2 1 3 4

у -1 -2 1 7 8

- нанесем точки на координатную плоскость и соединим последовательно.

Графиком линейно-кусочной функции является ломанная с бесконечными крайними звеньями (слайд 12) .

Рисунок 7

Каким же методом график получается быстрее и легче?

3. Чтобы закрепить данный метод предлагаю выполнить следующее задание:

При каких значения х функция у=|х-2|-|х+1| принимает наибольшее значение.

Следуем алгоритму; ученик на доске.

у=|х-2|-|х+1|

х₁=2, х₂=-1

у(-2)=4-1=3

у(-1)=3

у(2)=-3

у(3)=1-4=3, соединяем последовательно точки.

у_наиб = 3

4. Дополнительное задание

При каких значениях а уравнение ||4+x|-|x-2||=a имеет два корня.

5. Домашняя работа

а) При каких значениях Х функция у =|2x+3|+3|x-1|-|x+2| принимает наименьшее значение.

б) Построить график функции y=||x-1|-2|-3| .