У любого учителя математики рано или поздно возникает вопрос: нельзя ли соединить в одном уроке алгебру и геометрию, чтобы продемонстрировать неразрывную связь этих двух дисциплин? Данный материал позволяет сделать это в течение одного занятия.
Обычная практика проведения подобных уроков включает в себя большой теоретический и практический материал, дополненный небольшой презентацией. План проведения данного занятия основан на деятельном методе, побуждающем учеников самостоятельно формулировать тему урока и вести собственную исследовательскую деятельность.
Этапы урока состоят в следующем:
- Наводящие вопросы и факты, приводящие к постановке учебной задачи.
- Открытие учащимися нового знания.
- Первичный комментарий, обсуждение материала.
- Самостоятельная работа с проверкой полученных данных.
- Решение подобных задач.
- Контроль.
- Рефлексия.
Однако форма проведения данного занятия несколько отличается от стандартного в силу интегрированности двух математических дисциплин. Презентация теперь не играет роль дополнительного украшения, а является основой, главным элементом, на котором базируются этапы урока.
Итак, презентация открыта, урок начинается (заголовок, слайд №1).
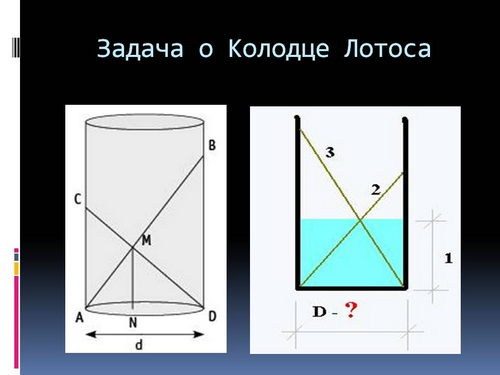
- 1 этап. На слайдах 2 и 3 описана задача, пришедшая к нам из Древнего Египта. Краткий экскурс в историю, закрепление межпредметных связей позволяет заинтересовать ребят новым материалом.
- 2 этап. Ученики обсуждают формулировку и внимательно изучают текст (слайды 4 и 5). Как правило, это время для обсуждения и обдумывания условий задачи, возможностей ее решения. На этом этапе создается первичный чертеж.
- 3 этап. Комментарий учителя (слайды 6 и 7) позволяет привлечь внимание к художественной литературе. Краткий пересказ рассказа А.П.Казанцева "Колодец Лотоса" всегда вызывает повышенный интерес, а условия прохождения испытания, когда кандидат в жрецы был замурован и мог выйти только в случае правильного ответа, невольно заставляет каждого примерить эту ситуацию на себя.
- 4 этап. Непосредственный вывод уравнения четвертой степени (слайды 8, 9, 10 и 11). Как правило, для этого необходимо применить лишь теорему Пифагора и использовать дополнительный материал (слайд 12).
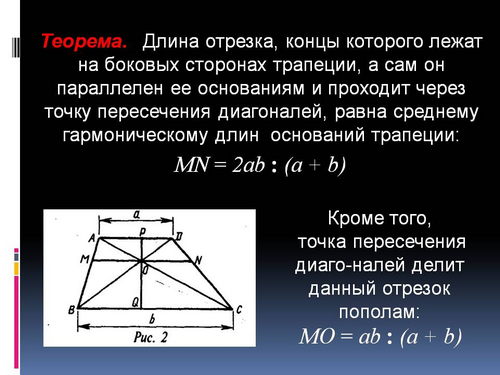
Теорема. Длина отрезка, концы которого лежат на боковых сторонах трапеции, а сам он параллелен ее основаниям и проходит через точку пересечения диагоналей, равна среднему гармоническому длин оснований трапеции. Кроме того, точка пересечения диагоналей делит данный отрезок пополам (см. рис. 2 на слайде 12).
Доказательство. Пусть РQ - высота трапеции. Из подобия треугольников АОD и СОВ следует, что РО: а = OQ : b. Или РО: а == (РQ - РО) :b. Отсюда легко получить, что РО = РQ * а: (а + b). Из подобия треугольников АВС и АМО следует пропорция РО : РQ = МО:b. А значит, МО = a * b : (а + b). То же самое вычисление действительно и для ОN.Легко установить, что МО = ОNи МN = 2аb : (а + b). А это и есть среднее гармоническое оснований.Теорема доказана.
Таким образом, получаем два равенства: a * b: (а + b)=1и 32 - b2 = 22 - а2.
Коллективная работа ребят у доски и в тетрадях позволяет легко вывести искомое уравнение.
- 5 этап. Ученики пытаются найти корень с помощью теоремы Безу, вспоминая материал 9-го класса. Попытки оценить значение корня с помощью производной (в 11 классе) также дает положительный эффект в плане повторения раздела исследования функций с помощью производной.
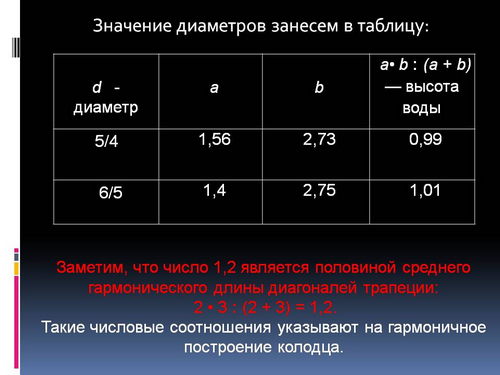
- 6 этап. Проверка полученных результатов (слайды 13, 14 и 15). Учащиеся убеждаются, что полученный ответ имеет лишь приблизительное значение. К тому же в Древнем Египте задачи не решались алгебраически, а применялся геометрический подход.
- 7 этап. Подводя итог урока, учитель вместе с учениками проговаривает примененные методы и знания, а также дает краткую оценку проведенной ими самостоятельной работы. С помощь последнего слайда № 16 стимулируется исследовательский интерес сильных учеников к новому решению исторической задачи о Колодце Лотоса.
Конечно, подобный урок не может быть регулярным или плановым. Его применения возможно в случае дополнительного или факультативного занятия, кружка заинтересованных ребят. Однако такие уроки позволяют не превратить изучения математики в смертельную скуку, расширяют кругозор учащихся, способствуют активации их исследовательской деятельности. Связь между различными предметами школьного курса, такими как история, информатика, алгебра, геометрия, литература, становится убедительной и неразрывной.
По опыту знаю, что подобные задачи и факты больше всего запоминаются учениками по окончании школы. К тому же масштаб такой деятельности позволяет продемонстрировать ребятам глубину интеллекта учителя, его многогранность и универсальность. Ведь все это в конечном итоге способствует повышению авторитета педагога третьего тысячелетия.