Цель мероприятия:
- повысить уровень математического развития учащихся и расширить их кругозор;
- развивать у учащихся интерес к занятиям математикой;
- углубить представление обучающихся об использовании сведений из математики в повседневной жизни;
- воспитывать самостоятельность мышления, волю, упорство в достижении цели, чувство ответственности и коллективизма.
В игре принимают участие команды учащихся 8-х классов в количестве 4–5 человек. Заранее определяется счетная комиссия из учителей, учеников и их родителей.
Оборудование: презентация, составленная по материалам к каждому гейму, секундомер, бочка с бочонками, музыкальное оформление, грамоты.
Ход мероприятия
1 этап. Вступительное слово.
Слайд 1
Ведущий: Добрый день, дорогие друзья! Добрый день, дорогие ребята, уважаемые взрослые! Я рад приветствовать вас на математической игре «счастливый случай»! Наши команды приготовились идти по нелёгкому пути к победе. И для того, чтобы сегодня выиграть, не забывайте пословицы: «Обдумай раньше, чем дело начать», «Видит око далеко, а ум дальше». Пусть Математика и Удача принесут вам, ребята, Счастливый случай!
2 этап. Первый гейм «Дальше… дальше… дальше…»
Слайд 2
Вопросы первой команде:
- Чему равен арифметический квадратный корень из 121? ( 11)
- Найти корень уравнения х2 = – 8? (корней нет)
- Чему равна площадь круга с радиусом R? (S = 2
) - Как называется угол, вершина которого лежит на окружности, а стороны пересекают окружность? (вписанный)
- Может ли угол параллелограмма быть равен 2000? (нет)
Вопросы второй команде:
- Чему равно произведение чисел 7, 8 и 125? (7000).
- Четырехугольник, у которого две стороны параллельны, а две другие нет? (трапеция)
- Как называется четырехугольник, площадь которого равна произведению смежных сторон? (прямоугольник)
- Отношение противолежащего катета к гипотенузе называется …? (синус острого угла прямоугольного треугольника)
- Что собой представляет график функции
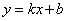? (прямая)
Вопросы третьей команде:
- Отношение прилежащего катета к гипотенузе называется …? (косинус острого угла прямоугольного треугольника)
- Как называется четырехугольник, у которого диагонали взаимно перпендикулярны, точкой пересечения делятся пополам и являются биссектрисами его углов? (ромб)
- Прямая, имеющая одну общую точку с окружностью, называется…? (касательной)
- Что больше 5 или
? (
) - Что является графиком функции
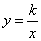? (гипербола)
Вопросы четвёртой команде:
- Чему равна четверть часа? (15 минут)
- Чему равна площадь параллелограмма? (Произведению его основания на высоту, проведённую к этому основанию)
- Как измеряется вписанный угол в окружность? (Половиной дуги, на которую он опирается)
- Отношение противолежащего катета к прилежащему катету называется …? (тангенсом острого угла прямоугольного треугольника)
- Значение переменной, при котором уравнение обращается в верное числовое равенство? (корень)
3 этап. Второй гейм «Гонка за лидером» – игра «Перевёртыши»
Слайд 3
Эта игра заключается в том, что слова какой – нибудь известной фразы, например, пословицы, заменяются антонимами. Выигрывает тот, кто первым разгадает настоящую фразу. Например, «Зайцев пугать – с опушки бежать». Какая пословица зашифрована? Ответ: «Волков бояться – в лес не ходить».
В нашем гейме будут «зашифрованы» математические выражения. Не все математические термины имеют антонимы, поэтому заменяем слова по принципу: «квадрат» – «куб», «параллельный» – «перпендикулярный», «площадь» – «периметр» и т.д.
- Умножать на 1 можно! (Делить на 0 нельзя!) Слайд 4
- Неправильное целое больше 0. (Правильная дробь меньше 1) Слайд 5
- Кривая дуга больше свёрнутой. (Прямой угол меньше развёрнутого) Слайд 6
- Перпендикулярные отрезки скрещиваются. (Параллельные прямые не пересекаются) Слайд 7
- Периметр треугольника не равен кубу чужого угла (Площадь квадрата равна квадрату его стороны) Слайд 8
4 этап. Третий гейм «Заморочки из бочки»
Слайд 9
Каждая команда получает один бочонок с номером задания и решает его.
- Вычислите
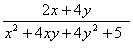, если x+2y=5. [
] - Упростите выражение
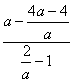. [2-a] - Известно, что x +
=2,5. Не вычисляя x, найдите х2 + 
. [4,25] - Сережа пришел к своему другу Диме.
– Что же ты у нас не был вчера? – Спросил Дима. – Ведь вчера моя бабушка праздновала день рождения.
– Я не знал, – сказал Сережа – А сколько лет твоей бабушке?
Дима ответил замысловато:
– Моя бабушка говорит, что в её жизни не было такого случая, чтобы не справлялся её день рождения. Вчера она праздновала этот день в 15-й раз. Вот сколько лет моей бабушке? [60 лет]
V этап. Четвёртый гейм «Тёмная лошадка»
Слайд 10
I уровень
Перед вами портреты великих людей: Льва Николаевича Толстого, Михаила Васильевича Ломоносова и Александра Сергеевича Пушкина.
Вопрос 1: Кто из этих знаменитых людей сделал интересное и меткое «арифметическое сравнение», что человек подобен дроби, числитель которой есть то, что человек представляет собой, а знаменатель – то, что он думает о себе. Чем большего мнения о себе человек, тем больше знаменатель, а значит, тем меньше дробь? (Л.Н. Толстой) Слайд 11
Вопрос 2: По чьему проекту в 1755 году был организован Московский университет, носящий его имя ныне? (М.В. Ломоносов) Слайд 12
Вопрос 3: Кто из них является автором учебника для детей под названием «Арифметика»? (Л.Н. Толстой для детей Яснополянской школы) Слайд 13
II уровень
Перед вами портреты древнегреческих учёных, живших в VI – III вв. до н.э., Пифагора, Архимеда, Фалеса.
Вопрос 1: Кто из ученых сформулировал следующие теоремы: «Вертикальные углы равны», «В равнобедренном треугольнике углы при основании равны», «Диаметр делит круг пополам» и др.? (Фалес) Слайд 14
Вопрос 2: кто из ученых помогал защищать свой город Сиракузы от римлян и при этом погиб? Легенда гласит: когда римлянин занёс меч над ученым, тот не просил пощады, а лишь воскликнул: «Не трогай мои чертежи!» В миг гибели учёный решал геометрическую задачу. (Архимед) Слайд 15
Вопрос 3: Кому из них принадлежат слова «Числа правят миром»? (Пифагор) Слайд 16
III уровень
Слайд 17
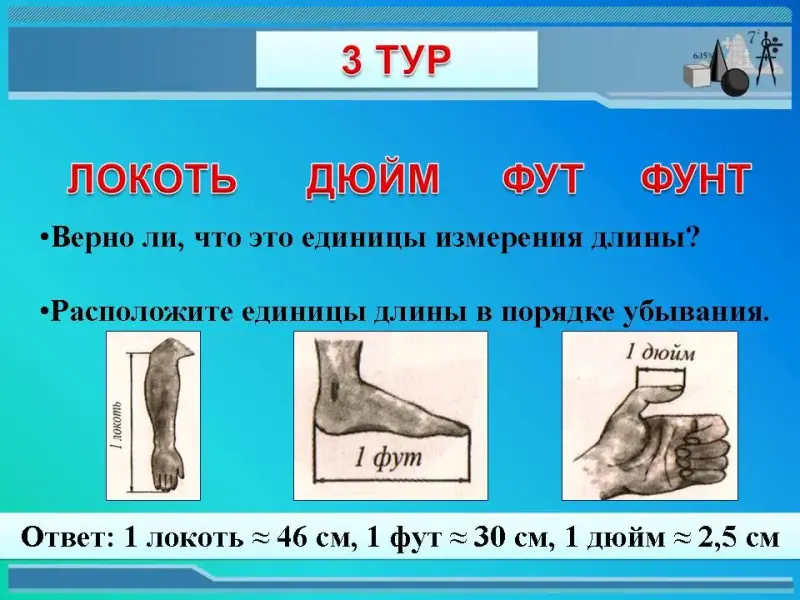
| ЛОКОТЬ | ДЮЙМ | ФУТ | ФУНТ |
Вопрос 1: Верно ли, что это единицы измерения длины?
Ответ: нет, фунт – единица веса и счетно – денежная единица.
Вопрос 2: Расположите единицы длины в порядке убывания.
Ответ: 1 локоть 
, 1 фут 
,1 дюйм 
6 этап. Пятый гейм «Ты – мне, я – тебе»
Слайд 18
Объявление для всех!
Конкурсантов ждет успех!
Построенье выполняйте, счет команды пополняйте.
Задача конкурса: совместными усилиями в атмосфере взаимопомощи выполнить построение на координатной прямой.
Отметить на координатной плоскости точки и последовательно соединить.
(-9;-1); (-2;-5); (0;5); (2;3); (2;1); (0;-1); (-;-1); (-5;-5); (-6;-5); (-9;-8); (-11;-9); (-8;-5); (-12;-8); (-10; -5); (-12:-6); (-10;-4); (-12;-4); (-11;-1); (-11;2); (-6;6); (-4;7); (-4;10); (-2;12); (-3;12); (-1;14); (0;14); (-1;15); (0;15); (1;14); (1;16); (2;15); (2;16); (3;15); (3;16); (4;15); (4;16); (6;14); (6;8); (7;8); (6;7); (7;6); (6;6); (5;5); (5;0); (4;-1); (4;-2); (-1;-7); (-5;-9); (-12;-17); (-11; -14); (-13;15); (-11;-12); (-12;-12); (-10;-10); (-9;-8); (2;10).
Во время выполнения задания пятого гейма зрителям предлагаются вопросы и старинные задачи.
ВОПРОСЫ ДЛЯ ЗРИТЕЛЕЙ
- Как называется четвёртая буква греческого алфавита? (Дельта)
- Чему равна сумма внутренних углов четырехугольника? (360 градусов)
- У людей какой профессии постоянно перед глазами пять параллельных линий? (Музыканты. Нотный стан имеет пять линий)
- Как на языке геометрии будет называться правильный шестигранник? (Гексаэдр, или куб)
- Какой древний город по преданию стоял на 7 холмах? (Рим)
- В какой спортивной игре, изобретённой в 1895 году в США В.Морганом, на площадке играют команды, состоящие из шести человек? (Волейбол)
- Какой угол образуют часовые стрелки, когда на часах 6.00? (Развёрнутый)
- В каком городе мира впервые стали отмерять ход времени семидневными неделями? (Вавилон)
- Какую приставку обычно употребляют физики и математики, когда видят число 106? (Мега…)
- Какую процедуру народная мудрость советует совершить семь раз, прежде чем один раз совершить другую процедуру? («Семь раз отмерь, один раз отрежь»)
Старинные задачи для зала
- Шла баба в Москву и повстречала трех мужиков. Каждый из них нес по мешку, в каждом мешке по кошке. Сколько существ направлялось в Москву? [1]
- Торговка, сидя на рынке, соображала: «Если бы к моим яблокам прибавить половину да ещё десяточек, то у меня была бы целая сотня. Сколько яблок у нее было? [60]
- Брат и сестра получили в наследство 90 тыс. рублей. Если сестра отдаст брату из своей доли 10 тыс. рублей, то брат окажется вдвое богаче своей сестры. Сколько денег досталось брату и сестре? [брат – 50000, сестра – 40000]
- Две богомолки отправились в Троице-Сергиеву Лавру. Обе они прошли 60 вёрст. Сколько верст прошла каждая, если шли с одинаковой скоростью? [60 вёрст]
- Арбуз стоит 100 рублей и ещё пол-арбуза. Сколько стоит арбуз? [200 руб.]
- 6 рыбаков съели 6 судаков за 6 дней. За сколько дней 10 рыбаков съедят 10 судаков? [6 дней]
- В классе 35 учеников. Мальчиков на три больше, чем девочек. Сколько мальчиков и сколько девочек? [19 мальчиков и 16 девочек]
- Горело 5 свечей. Две из них потушили. Сколько свечей останется? [2]
- Угол в 1о рассматривают в лупу, дающую четырехкратное увеличение. Какой величины окажется угол. [1о]
- Заглавия каких литературных произведений начинаются с чисел 3, 20, 80, 20000, 12, 2?
- На дереве сидело 10 птиц. Охотник выстрелил и подстрелил одну птицу. Сколько птиц осталось на дереве. [Ни одной]
- Тройка лошадей пробежала 30 км. Сколько километров пробежала каждая лошадь? [30 км]
7 этап. Подведение итогов игры. Награждение победителей.
Литература:
- Альхова З.Н., Макеева А.В. Внеклассная работа по математике. – Саратов: «Лице», 2002.
- Волошинов А.В. Пифагор: союз истины, добра и красоты. – М.: Просвещение, 1993.
- Карпеев Э.И. Михаил Васильевич Ломоносов: Книга для учащихся. – М.: Просвещение, 1997.
- Козлова Е.Г. Сказки и подсказки. – М.: Просвещение, 1994.
- Математика. Предметная неделя в школе/ авт.-сост.: Г.И.Григорьева. – М.: Глобус, 2008.
- Фарков А.В. Математические кружки в школе. – Волгоград: Учитель, 2007.
- Час занимательной математики/ Под ред. Л.Я.Фальке. – М.: Илекса; Народное образование, 2003.