Методы решения тригонометрических уравнений
Урок комплексного применения знаний.
Цели урока.
- Рассмотреть различные методы решения тригонометрических уравнений.
- Развитие творческих способностей учеников путем решения уравнений.
- Побуждение учеников к самоконтролю, взаимоконтролю, самоанализу своей учебной деятельности.
Оборудование: экран, проектор, справочный материал.
Ход урока
Вводная беседа.
I.
Основным методом решения тригонометрических уравнений является сведения их простейшим. При этом применяются обычные способы, например, разложения на множители, а также приемы, используемые только для решения тригонометрических уравнений. Этих приемов довольно много, например, различные тригонометрические подстановки, преобразования углов, преобразования тригонометрических функций. Беспорядочное применение каких-либо тригонометрических преобразований обычно не упрощает уравнение, а катастрофически его усложняет. Чтобы выработать в общих чертах план решения уравнения, наметить путь сведения уравнения к простейшему, нужно в первую очередь проанализировать углы - аргументы тригонометрических функций, входящих в уравнение.
Сегодня мы поговорим о методах решения тригонометрических уравнений. Правильно выбранный метод часто позволяет существенно упростить решение, поэтому все изученные нами методы всегда нужно держать в зоне своего внимания, чтобы решать тригонометрические уравнения наиболее подходящим методом.
II. (С помощью проектора повторяем методы решения уравнений.)
1. Метод приведения тригонометрического уравнения к алгебраическому.
Необходимо выразить все тригонометрические функции через одну, с одним и тем же аргументом. Это можно сделать с помощью основного тригонометрического тождества и его следствий. Получим уравнение с одной тригонометрической функцией. Приняв ее за новую неизвестную, получим алгебраическое уравнение. Находим его корни и возвращаемся к старой неизвестной, решая простейшие тригонометрические уравнения.

2. Метод разложения на множители.
Для изменения углов часто бывают полезны формулы приведения, суммы и разности аргументов, а также формулы преобразования суммы (разности) тригонометрических функций в произведение и наоборот.
sin x + sin 3x = sin 2x + sin4x
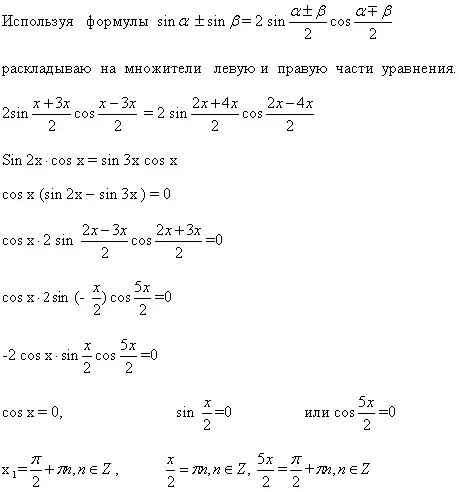

3. Метод введения дополнительного угла.

4. Метод использования универсальной подстановки.
Уравнения вида F(sinx, cosx, tgx ) = 0 сводятся к алгебраическому при помощи универсальной тригонометрической подстановки ![]()
Выразив синус, косинус и тангенс через тангенс половинного угла. Этот прием может привести к уравнению высокого порядка. Решение которого затруднительно.

5. Метод понижения степени.

III. Самостоятельная работа (программированный контроль).
| 1-й вариант | 2-й вариант |
| 1) 2cos2x + 2sin x = 2,5
2) sin2x = -cos2x 3) (cosx - sinx)2 = cos2x |
1) 2sin2x + 5cosx + 1 = 0
2) sin2x - sin3x = 0 3) sin2x = 2 |
Таблица ответов.


Коды ответов:1-й вариант: 524, 2-й вариант: 361.
IV. Домашнее задание.
Решить следующие уравнения:
