Тип урока
: урок обобщения и комплексных применений знаний, умений и навыков по теме “Показательные уравнения и способы их решения”.Цели урока.
Оборудование:
компьютер и мультимедийный проектор.На уроке используются информационные технологии: методическое обеспечение к уроку – презентация в программе Microsoft Power Point.
Ход урока
Всякое умение трудом даётся
I. Постановка цели урока (Слайд № 2)
На этом уроке подведём итог и обобщим тему “Показательные уравнения, их решения”. Познакомимся с типовыми заданиями ЕГЭ разных лет по данной теме.
Задачи на решение показательных уравнений могут встречаться в любой части заданий ЕГЭ. В части “В” обычно предлагают решить простейшие показательные уравнения. В части “С” можно встретить более сложные показательные уравнения, решение которых обычно является одним из этапов выполнения задания.
Например (Слайд № 3).
- ЕГЭ – 2007
В4 – Найдите наибольшее значение выражения х • у, где (х; у) – решение системы:

В1– Решить уравнения:
а) х • 63х – 36 • 63х = 0;
б) 4х +1 + 8 • 4х = 3.
В4 – Найдите значение выражения х + у, где (х; у) – решение системы:

- ЕГЭ – 2010
В3
– Решите уравнение: 7х – 2 = 49.С1
– Найдите корни уравнения: 4х2 + 3х – 2 - 0,52х2 + 2х – 1 = 0.С3
– Решите систему уравнений:
II. Актуализация опорных знаний. Повторение
(Слайды № 4 – 6 презентации к уроку)На экран демонстрируется опорный конспект теоретического материала по теме.
Обсуждаются следующие вопросы:
- Какие уравнения называются показательными?
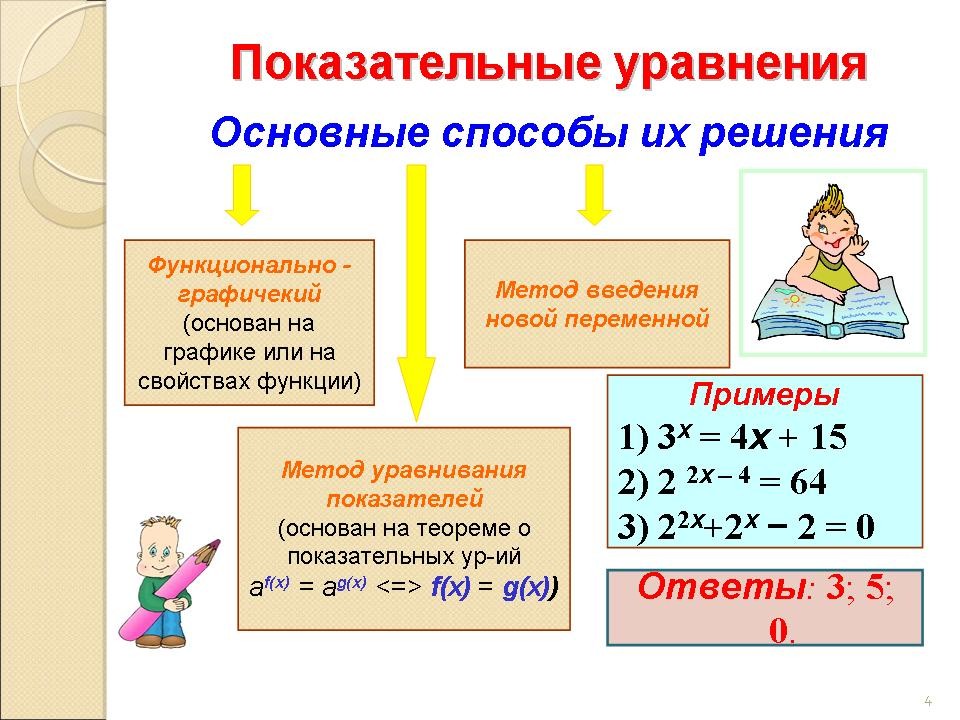
- Назвать основные способы их решения. Привести примеры их видов (Слайд № 4)
- Какую теорему используют при решении простейших показательных уравнений вида: а f(x) = a g(x)?
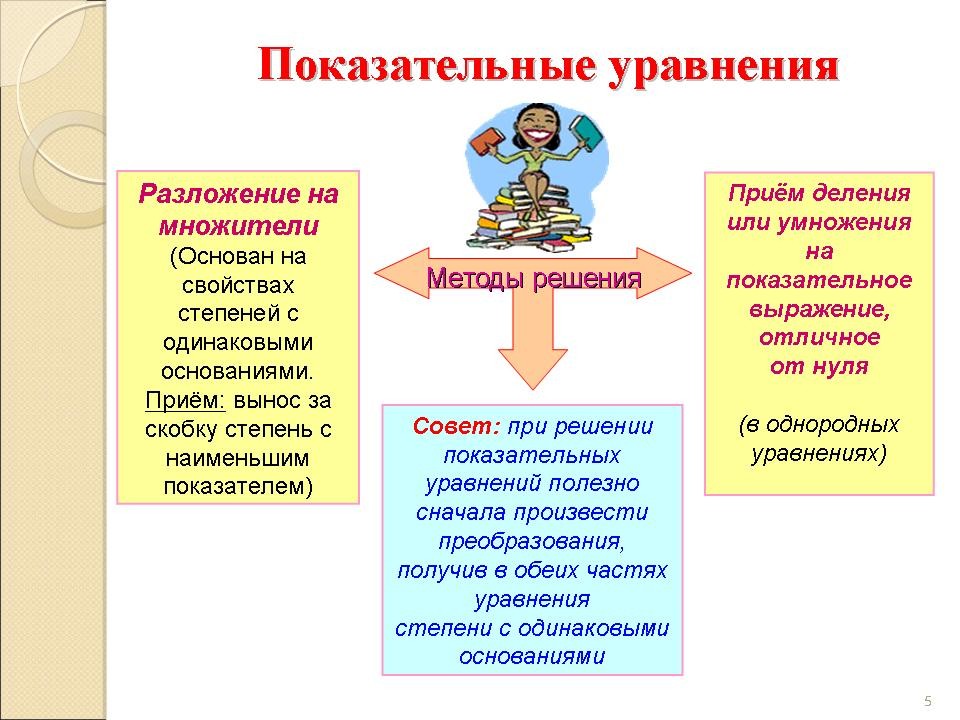
- Какие ещё методы решения показательных уравнений существуют? (Слайд № 5)
(Самостоятельно решить предлагаемые уравнения к каждому способу и выполнить самопроверку с помощью слайда)
- Метод разложения на множители (основан на свойствах степеней с одинаковыми основаниями, приём: выносится за скобку степень с наименьшим показателем).
- Приём деления (умножения) на показательное выражение, отличное от нуля, при решении однородных показательных уравнений .
- Совет:
-
Решение уравнений двумя последними методами
с последующими комментариями
(Слайд № 6).
Пример
. 4х + 1 – 2 • 4х – 2 = 124, 4х – 2 • (43 - 2) = 124, 4х – 2 • 62 = 124,4 х – 2 = 2, 4 х – 2 = 4 0,5, х – 2 = 0,5, х = 2,5.
Пример.
2 • 22х – 3 • 2х • 5х – 5 • 52х = 0¦: 52х2 • (2/5)2х – 3 • (2/5) х - 5 = 0,
t = (2/5)х, t > 0, 2t2 - 3 t - 5 = 0, t = -1(?...), t = 5/2; 5/2 = (2/5)х , х = ?...
III. Решение заданий ЕГЭ 2010
Учащиеся самостоятельно решают предлагаемые в начале урока на слайде № 3 задания, используя указания к решению, проверяют свой ход решения и ответы к ним с помощью презентации (Слайд № 7). В процессе работы обсуждаются варианты и способы решения, обращается внимание на возможные ошибки при решении.
В3
: а) 7х – 2 = 49, б) (1/6)12 – 7 х = 36. Ответ: а) х = 4, б) х = 2.С1
: 4х2 + 3х – 2 - 0,52х2 + 2х – 1 = 0. (Можно заменить 0,5 = 4– 0,5)Решение. ![]() ,
,
х2 + 3х – 2 = -х2 - 4х + 0,5 …
Ответ: х = -5/2, х = 1/2.
С3
: 5 • 5tgy + 4 = 5-tgy, при сos y < 0.Указание к решению
. 5 • 5tgy + 4 = 5 -tgy ¦•5tgy5 • 52gy + 4 • 5 tgy – 1 = 0. Пусть х = 5 tgy , …
5tgy = -1 (?...), 5tgy =1/5.
Так как tgy = -1 и сos y < 0, то у ![]() II координатной
четверти
II координатной
четверти
Ответ: у = 3![]() /4 + 2
/4 + 2![]() k, k
k, k ![]() N.
N.
IV. Совместная работа у доски
Рассматривается задание высокого уровня обученности – Слайд № 8. С помощью данного слайда происходит диалог учителя и учащихся, способствующий развитию решения.
С5
– При каком параметре а уравнение 22х – 3 • 2х + а2 – 4а = 0 имеет два корня?Решение.
Пусть t = 2х, где t > 0. Получаем t 2 – 3t + (а2 – 4а) = 0 .
1). Так как уравнение имеет два корня, то D > 0;
2). Так как t1,2 > 0, то t1 • t2 > 0, то есть а2 – 4а > 0 (?...).
Значит,

Ответ: а ![]() (–
0,5; 0) или (4; 4,5).
(–
0,5; 0) или (4; 4,5).
V. Проверочная работа
(Слайд № 9)Учащиеся выполняют проверочную работу на листочках, осуществляя самоконтроль и самооценку выполненной работы с помощью презентации, утверждаясь в теме. Самостоятельно определяют для себя программу регулирования и коррекции знаний по допущенным ошибкам в рабочих тетрадях. Листы с выполненной самостоятельной работой сдаются учителю на проверку.
Подчёркнутые номера – базового уровня, со звёздочкой – повышенной сложности.

Решение и ответы.
3. 2х – 1(5 • 2 4 - 4) = 19, 2х – 1 • 76 = 19, 2х – 1 = 1/4, 2х – 1 = 2 – 2, х – 1 = -2,
х = -1.
4*. 3 • 9х = 2 • 3х • 5х + 5 • 25х | : 25х,
3 • (9/25)х = 2 • (3/5)х + 5,
3 • (9/27)х = 2 • (3/5)х + 5 = 0,
3 • (3/5)2х – 2 • (3/5)х - 5 = 0,…, (3/5) х = -1 (не подходит),
(3/5)х = 5, х = -1.
VI. Задание на дом
(Слайд № 10)- Повторить § 11, 12.
- Из материалов ЕГЭ 2008 – 2010 г. выбрать задания по теме и решить их.
- Домашняя проверочная работа :