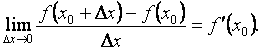Производная в физике
Алгебра щедра. Зачастую она дает больше, чем у нее спрашивают.
Ж.Даламбер
Межпредметные связи являются дидактическим условием и средством глубокого и всестороннего усвоения основ наук в школе.
Кроме того, они способствуют повышению научного уровня знаний учащихся, развитию логического мышления и их творческих способностей. Реализация межпредметных связей устраняет дублирование в изучении
материала, экономит время и создаёт благоприятные условия для формирования общеучебных умений и навыков учащихся.
Установление межпредметных связей в курсе физики повышает эффективность политехнической и практической направленности обучения.
В преподавании математики очень важна мотивационная сторона. Математическая задача воспринимается учащимися лучше, если она возникает как бы у них на глазах, формулируется после рассмотрения каких-то
физических явлений или технических проблем.
Сколько бы ни говорил учитель о роли практики в прогрессе математики и о значении математики для изучения физики, развития техники, но если он не показывает, как физика влияет на развитие математики
и как математика помогает практике в решении её проблем, то развитию материалистического мировоззрения будет нанесен серьёзный ущерб. Но для того, чтобы показать, как математика помогает в решении её
проблем, нужны задачи, не придуманные в методических целях, а возникающие на самом деле в различных областях практической деятельности человека
Исторические сведения
Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач:
- о разыскании касательной к произвольной линии;
- о разыскании скорости при произвольном законе движения.
 |
 |
Еще раньше понятие производной встречалось в работах итальянского математика Николо Тартальи (около 1500 - 1557гг.) - здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.

В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной.

Посвящает целый трактат о роли производной в математике известный учёный Галилео Галилей. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л.Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.
| Термин «производная» является буквальным переводом на русский французского слова derive, которое ввел в1797 году Ж. Лагранж (1736-1813).
И.Ньютон называл производную функцию флюксией, а саму функцию - флюентой. |
Некоторые применения производной в физике
Производная - основное понятие дифференциального исчисления, характеризующее скорость изменения функции.
Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.
Таким образом, 
Значит, чтобы вычислить производную функции f(x) в точке x0 по определению, нужно:
|
Рассмотрим несколько физических задач, при решении которых применяется эта схема.
Задача о мгновенной скорости. Механический смысл производной
Напомним, как определялась скорость движения. Материальная точка движется по координатной прямой. Координата х этой точки есть известная функция x(t) времени t. За промежуток
времени от t0 до t0 + ![]() перемещение точки равно x(t0 +
перемещение точки равно x(t0 + ![]() ) - x(t0) - а её средняя скорость такова:
) - x(t0) - а её средняя скорость такова: ![]() .
.
Обычно характер движения бывает таковым, что при малых ![]() , средняя скорость практически не меняется, т.е. движение с большой степенью точности
можно считать равномерным. Другими словами, значение средней скорости при
, средняя скорость практически не меняется, т.е. движение с большой степенью точности
можно считать равномерным. Другими словами, значение средней скорости при ![]() стремится к некоторому вполне определённому значению, которое
называют мгновенной скоростью v(t0) материальной точки в момент времени t0.
стремится к некоторому вполне определённому значению, которое
называют мгновенной скоростью v(t0) материальной точки в момент времени t0.
Итак, ![]()
Но по определению ![]()
Поэтому считают, что мгновенная скорость в момент времени t0 ![]()
| Коротко говорят: производная координаты по времени есть скорость. В этом состоит механический смысл производной. |
Аналогично рассуждая, получаем, что производная от скорости по времени есть ускорение, т.е. ![]()
Задача о теплоемкости тела
Чтобы температура тела массой в 1г повысилась от 0 градусов до t градусов, телу необходимо сообщить определенное количество тепла Q. Значит, Q есть функция температуры
t, до которой тело нагревается: Q = Q(t). Пусть температура тела повысилась с t0 до t. Количество тепла, затраченное для этого нагревания, равно ![]() Отношение
Отношение ![]() есть количество тепла, которое необходимо в среднем для нагревания тела на 1 градус
при изменении температуры на
есть количество тепла, которое необходимо в среднем для нагревания тела на 1 градус
при изменении температуры на ![]() градусов. Это отношение называется средней теплоёмкостью данного тела и обозначается сср.
градусов. Это отношение называется средней теплоёмкостью данного тела и обозначается сср.
Т.к. средняя теплоёмкость не дает представления о теплоёмкости для любого значения температуры Т, то вводится понятие теплоёмкости при данной температуре t0 (в данной точке
t0).
Теплоемкостью при температуре t0 (в данной точке) называется предел
| Коротко говорят: производная от количества тепла, получаемого телом, по температуре есть теплоемкость. |
Задача о линейной плотности стержня
Рассмотрим неоднородный стержень.
| Стержень называют неоднородным, если на два участка одинаковой длины приходятся различные массы. |
Для такого стержня встаёт вопрос о скорости изменения массы в зависимости от его длины.
Средняя линейная плотность ![]() масса стержня есть функция его длины х.
масса стержня есть функция его длины х.
Таким образом, линейная плотность неоднородного стержня в данной точке определяется следующим образом: ![]()
| Коротко говорят: линейная плотность стержня в точке есть производная массы по длине. |
Рассматривая подобные задачи, можно получить аналогичные выводы по многим физическим процессам. Некоторые из них приведены в таблице.
|
Функция |
Формула |
Вывод |
| m(t) - зависимость массы расходуемого горючего от времени. | Производная массы по времени есть скорость расхода горючего. | |
| T(t) - зависимость температуры нагреваемого тела от времени. | Производная температуры по времени есть скорость нагрева тела. | |
| m(t) - зависимость массы при распаде радиоактивного вещества от времени. | Производная массы радиоактивного вещества по времени есть скорость радиоактивного распада. | |
| q(t) - зависимость количества электричества, протекающего через проводник, от времени | Производная количества электричества по времени есть сила тока. | |
| A(t) - зависимость работы от времени | Производная работы по времени есть мощность. |
Практические задания:
№1.
Снаряд, вылетевший из пушки, движется по закону x(t) = - 4t2 + 13t (м). Найти скорость снаряда в конце 3 секунды.
№2.
Количество электричества, протекающего через проводник, начиная с момента времени t = 0 c, задаётся формулой q(t) = 2t2 + 3t + 1 (Кул) Найдите силу тока в конце пятой секунды.
№3.
Количество тепла Q (Дж), необходимого для нагревания 1 кг воды от 0o до toС, определяется формулой Q(t) = t + 0,00002t2 + 0,0000003t3. Вычислите теплоемкость воды, если t = 100o.
№4.
Тело движется прямолинейно по закону х(t) = 3 + 2t + t2 (м). Определите его скорость и ускорение в моменты времени 1 с и 3 с.
№ 5.
Найдите величину силы F, действующей на точку массой m, движущуюся по закону х(t) = t2 - 4t4 (м), при t = 3 с.
№ 6.
Тело, масса которого m = 0,5кг, движется прямолинейно по закону х(t) = 2t2 + t - 3 (м). Найдите кинетическую энергию тела через 7 с после начала движения.
Заключение
Можно указать еще много задач из техники, для решения которых также необходимо отыскивать скорость изменения соответствующей функции.
Например, отыскание угловой скорости вращающегося тела, линейный коэффициент расширения тел при нагревании, скорость химической реакции в данный момент времени.
Ввиду обилия задач, приводящих к вычислению скорости изменения функции или, иначе, к вычислению предела отношения приращения функции к приращению аргумента, когда последнее стремится к нулю,
оказалось необходимым выделить такой предел для произвольной функции и изучить его основные свойства. Этот предел и назвали производной функции.
Итак, на ряде примеров мы показали, как различные физические процессы описываются с помощью математических задач, каким образом анализ решений позволяет делать выводы и предсказания о ходе
процессов.
Конечно, число примеров такого рода огромно, и довольно большая часть из них вполне доступна интересующимся учащимся.
"Музыка может возвышать или умиротворять душу,
Живопись - радовать глаз,
Поэзия - пробуждать чувства,
Философия - удовлетворять потребности разума,
Инженерное дело - совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей".
Так сказал американский математик Морис Клайн.
Список литературы :
- Абрамов А.Н., Виленкин Н.Я. и др. Избранные вопросы математики. 10 класс. - М: Просвещение, 1980.
- Виленкин Н.Я., Шибасов А.П. За страницами учебника математики. - М: Просвещение,1996.
- Доброхотова М.А., Сафонов А.Н. Функция, её предел и производная. - М: Просвещение, 1969.
- Колмогоров А.Н., Абрамов А.М. и др. Алгебра и начала математического анализа. - М: Просвещение, 2010.
- Колосов А.А. Книга для внеклассного чтения по математике. - М: Учпедгиз, 1963.
- Фихтенгольц Г.М. Основы математического анализа, ч.1 - М: Наука, 1955.
- Яковлев Г.Н. Математика для техникумов. Алгебра и начала анализа, ч.1 - М: Наука, 1987.