Обобщающий урок по алгебре по теме "Числовые функции, их свойства и графики". 9-й класс

Разделы: Математика

Класс: 9

Цели:

  • Обучающие: повторить, обобщить полученные знания по темам: “Функции y = xn, y = x -n, где n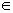N, y = 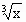, их свойства и графики”; закрепить навыки и умения учащихся в построении и чтении графиков функций (перечисления их свойств); формировать умение переносить известные приёмы и методы на решение более сложных, но типовых задач; проверить степень усвоения учащимися изученного материала.
  • Развивающие: активизировать мыслительный процесс учащихся, прививать интерес к предмету.
  • Воспитательные: развивать личностные качества учащихся (коммуникативность и самостоятельность, волю и упорство в достижении цели), воспитывать чувство уважения друг к другу.

Тип урока: Урок обобщения и систематизации знаний.

Оборудование:

  1. Интерактивное оборудование (ПК, мультимедийный проектор).
  2. Тест, материал в Microsoft Word (Приложение 1).
  3. Интерактивная программа “АвтоГраф”.
  4. Индивидуальный тест – раздаточный материал (Приложение 2).

Ход урока

1. Организационный момент

Озвучивается цель урока.

I этап урока

Проверка домашнего задания

  1. Собрать листочки с домашней самостоятельной работой из дидактического материала [2] С-19 вариант 1.
  2. Решить на доске задания, вызвавшие затруднения у учащихся при выполнении домашней самостоятельной работы.

II этап урока

1. Фронтальный опрос.

Ответьте на вопросы (Приложение 1, стр. 1)

  1. Приведите примеры функции вида y = xn, где n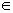N.
  2. Перечислите свойства функции y = x5, изобразив схематически график на доске.
  3. Приведите примеры функции вида y = x -n, где n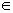N.
  4. Перечислите свойства функции y = x -2, изобразив схематически график на доске.
  5. Перечислите свойства функции y = 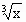, изобразив схематически график на доске.

2. Блиц-опрос: выделите на доске верный ответ в тесте (Приложение 1, стр. 2-3).

III этап урока

Выполнение упражнений.

1. Решить № 358 (а). Решите графически уравнение: .

Один ученик решает на доске, остальные в тетради. При необходимости учитель помогает ученику.

На интерактивной доске с помощью программы “АвтоГраф” построена прямоугольная система координат. Учащийся чертит соответствующие графики маркером, находит решение, записывает ответ. Затем задание проверяется: вводится формула с помощью клавиатуры, и график должен совпасть с уже нарисованным в этой же системе координат. Абсцисса пересечения графиков и есть корень уравнения.

2. Карточки (четыре слабых учащихся решают в тетради или на доске):

1) Найдите значение выражения: а) ; б) .

2) Найдите область определения функций: а) ; б) y = .

3. Решить № 358 (а). Решите графически уравнение: .

Один ученик решает на доске, остальные в тетради. При необходимости учитель помогает ученику.

На интерактивной доске с помощью программы “АвтоГраф” построена прямоугольная система координат. Учащийся чертит соответствующие графики маркером, находит решение, записывает ответ. Затем задание проверяется: вводится формула с помощью клавиатуры, и график должен совпасть с уже нарисованным в этой же системе координат. Абсцисса пересечения графиков и есть корень уравнения.

Решение:

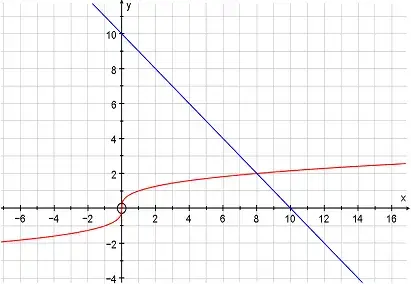
Ответ: 8

Решить № 360 (а). Постройте и прочитайте график функции: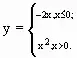

Учащиеся выполняют задание самостоятельно.

Проверяется построение графика с помощью программы “АвтоГраф”, свойства записываются на доске одним учащимся (область определения, область значения, чётность, монотонность, непрерывность, нули и знакопостоянство, наибольшее и наименьшее значения функции).

Решение:

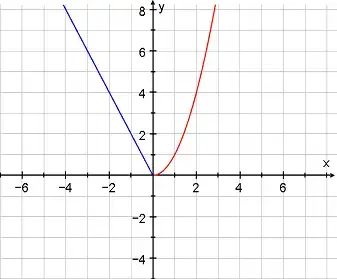
img2.gif (7885 bytes)

Свойства:

1) D(f) = (-); E(f) = [0; + );

2) ни чётная ни нечётная;

3) убывает на промежутке (-; 0], возрастает на [0; + );

4) непрерывна на R;

5) y = 0 при x = 0; y > 0 при xR;

6) y min = 0.

5. Решить № 348 (в). Решите графически неравенство: x-2 2x – 1.

Один из сильных учащихся решает на доске, остальные в тетради.
Проверяются построения графиков с помощью программы “АвтоГраф”.

Решение:

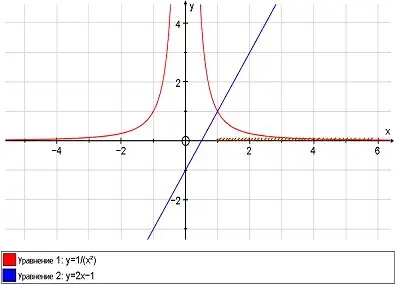
Ответ: x 1.

IV этап урока

Домашнее задание на следующий урок.

Без комментариев: учебник стр. 84 (домашняя контрольная работа № 3) № 1, 2, 7, 8, обязательно всем, № 9* дополнительно для желающих учиться на “5”.

V этап урока

Самостоятельная работа.

Тест: обведите один верный ответ из четырёх представленных (Приложение 2).

VII этап урока

Подведение итогов урока и выставление оценок.

Выставляются оценки за работу на уроке.

VIII этап урока

Рефлексия

Учитель желает знать, насколько самостоятельно и с какой уверенностью решал ученик задания. Для этого ученики ответят на вопросы теста (Приложение 3), а затем учитель обработает результаты.

Урок закончен. Спасибо за урок!

 Литература

  1. Алгебра. 9 кл.: В двух частях. Учебно-методический комплект для общеобразоват. учреждений. / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. – 7-е изд., перераб. – М.: Мнемозина, 2005.
  2. Алгебра 9 класс. Самостоятельные работы для учащихся общеобразовательных учреждений / Л.А. Александрова; под ред. А.Г. Мордковича. – 6-е изд. – М.: Мнемозина, 2009.
  3. Алгебра. 9 класс: поурочные планы по учебнику А.Г.Мордковича. – 2-е изд., стеротип. / авт.-сост. Т.Л. Афанасьева, Л.А. Тапилина. – Волгоград: Учитель, 2008.
  4. Алгебра: Тесты для 7 – 9 кл. общеобразовательных учреждений / А.Г. Мордкович, Е.Е. Тульчинская. – 5-е изд. – М.: Мнемозина, 2008.
  5. Интернет ресурсы: http//omc.mosuzedu.ru/content/view/336/122. Система подготовки к экзамену по алгебре в новой форме ГИА-9. Методист: Александрова Л.А.