Сумма углов треугольника. 5-й класс
Цель: Способствовать формированию у учащихся умения доказывать и доказать, что сумма углов треугольника равна 180º.
Задачи урока:
- Содействовать формированию у детей навыков измерения углов треугольника.
- Продолжить работу по формированию у школьников умения выполнять такие мыслительные операции, как классификация, обобщение, развитие мышления.
- Вызвать интерес к самостоятельной поисковой деятельности.
Оборудование: транспортир, угольник, плакаты с изображением различных видов углов, карточки с изображением треугольников, магниты.
Подготовил: учитель математики МОУ "Тат. Челнинская ООШ" Менделеевского муниципального района РТ Панкрашина Наталья Вячеславовна.
Ход урока
В начале урока учащиеся проговаривают слова:
"Да, путь познания не гладок,
Но знаем мы со школьных лет,
Загадок больше чем разгадок,
И поискам предела нет!"
Учитель оглашает тему и цель урока: выяснить, чему равна сумма углов треугольника.
На магнитной доске многоугольники.
- Ребята, разбейте на группы многоугольники (Шестиугольники, четырехугольники, треугольники.)
- Наиболее известная вам фигура из четырехугольников какая? Назовите ее? (Квадрат.)
- Какая фигура называется квадратом? (Квадратом называется фигура прямоугольник, у которого все стороны равны.)
- По каким элементам можно дать еще определение квадрата? (По углам.)
- Чему равны углы в квадрате? (90º)
- Сформулируйте полное определение квадрата. (Квадрат, это фигура, у которой все стороны равны и углы равны по 90º.)
- Чему равна сумма углов квадрата? (360)
- Как из квадрата получить 2 треугольника? (Провести диагональ.)
- Свойства диагонали проведенной в квадрате? (Диагональ проведенная в квадрате делит угол пополам..)
- Какие треугольники получились? (Прямоугольные, равные.)
Δ AВС = Δ АДС (по сторонам и углу В = углу Д = 90º)
- А чему равны углы в Δ АВС, Δ AДС. Можно найти? (Вспомогательное свойство диагонали.)
- Найдите сумму углов получившихся Δ-ов. (180º).

Вывод:
Сумма углов в прямоугольном треугольнике равна 180º.
- Ребята, а какие вам еще треугольники известны кроме прямоугольного? (Тупоугольный и остроугольный.)
- Дайте определение остроугольному треугольнику. (Треугольник у которого все углы острые, называется остроугольным.)
- Определение тупоугольного треугольника. (Треугольник у которого один угол тупой, называется тупоугольным.)
- А как вы думаете в остроугольном треугольнике (тупоугольном треугольнике) сумма углов равна 180 º?
- Хотите проверить?
У каждого учащегося на парте Δ.
(I вариант - остроугольные, II вариант - тупоугольные). Измеряют, убеждаются, что сумма углов равна 180º.
Вывод: В любом треугольнике сумма углов равна 180º.
1) Постройте в тетради произвольный треугольник. Измерьте углы.
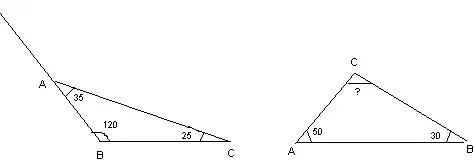
Постройте угол АВС = 120º. На сторонах угла отметьте отрезки, на ВС - 3 см, АВ - 2 см. Измерьте угол С, угол А. (угол С = 25º, угол А = 35º)
2) Постройте отрезок АВ, от точки А отложите угол 50º, от точки В отложите угол 30º. Найдите угол С, измерьте. (угол С = 100 º)
Практическая часть:
1. В Δ АВС угол В = 70º, угол А в два раза меньше угла В. Найдите величину угла С. (Рис. 1)
Решение:
1) 70:2 = 35º уголА
2) 180-(70+35) = 75º <С.
2. В прямоугольном Δ АВС угол С составляет 60º прямого угла. Найдите угол А. Постройте треугольник.
90 - 100%
? - 60%
90:100•60 = 54 - <С
180 - (90+54) = 36º - <А

3. Далее работа устно по карточкам (рис 2 - рис 6, см. Приложение) - вычисление углов.
Выводы урока, обобщение.
Д/з построить 3 треугольника:
- прямоугольный
- остроугольный
- тупоугольный.
Убедиться что сумма углов равна 180º.