Изучая математическую статистику в 7-м классе, важно наглядно представить учащимися образец для решения практических задач. Именно для этого мною был разработан данный справочный материал.
1.Представление данных.
1.1. Таблицы
Смета расходов на покупку спортивного инвентаря.
| № | Наименование | Ед. измерения | Количество | Цена (ед\руб) | Стоимость (руб) |
| 1 | Мяч футбольный | Шт. | 30 | 1000 |  |
| 2 | Мяч волейбольный | Шт. | 15 | 800 | 12000 |
| 3 | Ракетка | Шт. | 24 | 250 | 6000 |
| 4 | Воланы | коробка | 10 | 300 | 3000 |
| ИТОГО: | 51000 |
Таблицы предназначены для упорядочивания большого количества данных. Часто в таблицы заносят результаты вычислений, измерений.
1.2. Диаграммы.
За контрольную работу по математике школьники получили 6 оценок “отлично”, 10 оценок “хорошо”, 5 оценок “ удовлетворительно” и 3 оценки “не удовлетворительно”.
Столбиковая диаграмма.
Построим столбиковую диаграмму по этим данным.
Круговая диаграмма.
Построим круговую диаграмму по этим данным.
Для построения этой диаграммы мы:
- Разделили 360° на общее число учащихся (24)
- Затем последовательно умножаем 15° на количество учащихся, получивших ту или иную оценку.
- Затем круг делим на полученные сектора, подписываем данные.
360°\24=15° (такому углу соответствует оценка одного учащегося)
15°
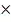6=90° -
сектор образованный этим углом соответствует
учащимся с оценкой “5”
15°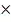10=150°
- сектор образованный этим углом соответствует
учащимся с оценкой “4”
15°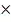5=75° -
сектор образованный этим углом соответствует
учащимся с оценкой “3”
15°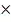3=45° -
сектор образованный этим углом соответствует
учащимся с оценкой “2”
Диаграмма рассеивания.
Для выявления связи между величинами применяются диаграммы рассеивания.
В таблице приведены данные о весе и росте 12 девушек.
Рост, см |
165 |
177 |
161 |
162 |
170 |
176 |
177 |
164 |
166 |
161 |
169 |
159 |
Х |
Вес, кг |
53 |
67 |
45 |
53 |
60 |
62 |
58 |
60 |
62 |
55 |
55 |
49 |
У |
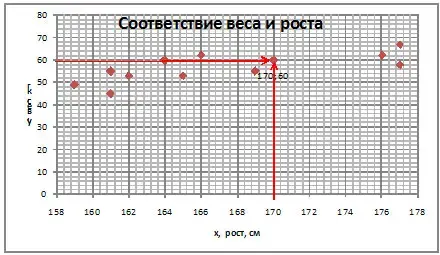
Для построения этой диаграммы нужно в системе координат поставить точки, абсциссы которых – рост, а ординаты – вес.
- Описательная статистика
2.1. Среднее значение
Определение:
Средним арифметическим нескольких чисел называется число, равное отношение суммы этих чисел к их количеству.Среднее арифметическое набора чисел х1,х2,х3,х4,х5
принято обозначать 
. Например, среднее арифметическое
пяти чисел запишется так:
Здесь в числителе дроби - сумма данных пяти чисел, а в знаменателе – их количество – 5.
Найти среднюю оценку учащегося по математике, если за истекший период он получил: 3, 4, 4, 5, 3, 2, 4, 3.
Запишем дробь и вычислим ее значение:
2.2. Медиана
Определение: Число, разделяющее набор чисел на две части, равные по численности, так что с одной стороны от этого числа все значения больше медианы, а с другой – меньше.
Метод вычисления медианы: Чтобы найти
медиану набора чисел нужно:
Найти медиану набора чисел: 9,3, 1, 5, 7.
Запишем числа в порядке возрастания.
1, 3, 5, 7, 9.
Здесь медиана набора число, стоящее посередине – 5.
Найти медиану набора чисел: 9,3, 1, 5, 7,8
Запишем числа в порядке возрастания.
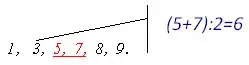
Выберем два центральных числа: 5 и 7. Найдем их полусумму: (5+7):2=6. То есть медиана данного набора есть число-6.
2.3. Наибольшее и наименьшее значение и размах.
Найти наибольшее, наименьшее значение и размах для ряда чисел:
12,7,25,3,19,15.
Очевидно, что наибольшим значением данного ряда является число 25, тогда как наименьшим число – 3. Найдем размах данного ряда.
Определение: Разность между наибольшим и наименьшим числом называется размахом набора чисел.
Размах показывает насколько велико рассеивание в числовом наборе. Итак, размах данного набора равен разности 25 и 3, т.е. 22.
2.4. Отклонение.
Определение: Отклонением данного значения от среднего арифметического значения данного набора является разность между этим числом и средним арифметическим. Соответственно если некоторое значение меньше среднего, то его отклонение отрицательно, если больше среднего – его отклонение положительно. Так же необходимо помнить, что сумма всех отклонений ряда чисел от среднего арифметического этих чисел равна нулю.
Составить таблицу отклонений от среднего арифметического для набора чисел: 2,4,5,7,10.
Вычислим среднее арифметическое этих чисел:
Составим таблицу отклонений.
| Число | Отклонение от среднего арифметического |
| 2 | 2-5,6= -3,6 |
| 4 | 4-5,6= -1,6 |
| 5 | 5-5,6= -0,6 |
| 7 | 7-5,6=1,4 |
| 10 | 10-5,6=4,4 |
2.5. Дисперсия.
Определение:
Среднее арифметическое квадратов отклонений от среднего значения называется дисперсией набора чисел. Дисперсию обозначают S2.В таблице представлены средние месячные температуры, в градусах. Вычислите дисперсию температуры за приведенный период.
| Месяцы | Январь | Февраль | Март | Апрель | Май |
| Средняя температура | -12 | -7 | 0 | 9 | 16 |
Решение:
- Вычислим среднюю температуру за 5 месецев.
- .Составим таблицу отклонений и их квадратов.
- Найдем среднее арифметическое для квадратов отклонений от среднего значения
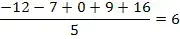
Итак, средняя температура составила 6 градусов.
| Число (температура) | Отклонение от среднего | Квадрат отклонения |
| -12 | -12-6=-18 | (-18)2=324 |
| -7 | -13 | 169 |
| 0 | -6 | 36 |
| 9 | 3 | 9 |
| 16 | 10 | 100 |
( последний столбец таблицы)
Итак, дисперсия средних температур за 5 месяцев составила 127,6. Ответ: S2=127,6
Составление таблицы изменений в процентах.
В таблице представлено количество продаваемых за неделю шоколадок в школьном буфете. Составьте таблицу изменения продаж по отношению к понедельнику в процентах.
День недели |
понедельник |
вторник |
среда |
четверг |
пятница |
суббота |
Количество |
50 |
46 |
89 |
71 |
44 |
32 |
Число проданных в понедельник шоколадок составляет 100% - эталон.
Вычислим, сколько составляет 1% эталона.
1% =50:100=0,5.
Вычислим, сколько процентов эталона составляет количество проданных шоколадок в другие дни недели.
Вторник – 46. Какой процент составляет 46 от 50. 46:0,5=92
Среда -89. 89 : 0,5= 178
Четверг – 71. 71 :0,5=142
Пятница – 44 44:0,5=88
Суббота -32 32 :0,5 =64
День недели |
понедельник |
вторник |
среда |
четверг |
пятница |
суббота |
Количество проданных шоколадок |
50 |
46 |
89 |
71 |
44 |
32 |
% от эталона |
100 |
92 |
178 |
142 |
88 |
64 |
Изменение продаж в % |
0 |
-8 |
78 |
42 |
-12 |
-36 |
