Урок-лекция для 8-го класса "Вероятности случайных событий"
Цель: ознакомить учащихся с правилами сложения и умножения вероятностей, понятием противоположных событий на кругах Эйлера.
Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.
Случайное явление - это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по иному.
Приведём примеры случайных событий: бросаются игральные кости, бросается монета, проводится стрельба по мишени и т.д.
Все приведённые примеры можно рассматривать под одним и тем же углом зрения: случайные вариации, неодинаковые результаты ряда опытов, основные условия которых остаются неизменными.
Совершенно очевидно, что в природе нет ни одного физического явления, в котором не присутствовали бы в той или иной степени элементы случайности. Как бы точно и подробно ни были фиксированы условия опыта, невозможно достигнуть того, чтобы при повторении опыта результаты полностью и в точности совпадали.
Случайные отклонения неизбежно сопутствуют любому закономерному явлению. Тем не менее, в ряде практических задач этими случайными элементами можно пренебречь, рассматривая вместо реального явления, его упрощённую схему «модель» и предполагая, что в данных условиях опыта явление протекает вполне определённым образом.
Однако существует ряд задач, где интересующий нас исход опыта зависит от столь большого числа факторов, что практически невозможно зарегистрировать и учесть все эти факторы.
Случайные события можно различным способом сочетать друг с другом. При этом образуются новые случайные события.
Для наглядного изображения событий используют диаграммы Эйлера. На каждой такой диаграмме прямоугольником изображают множество всех элементарных событий (рис.1). Все другие события изображают внутри прямоугольника в виде некоторой его части, ограниченной замкнутой линией. Обычно такие события изображают окружности или овалы внутри прямоугольника.
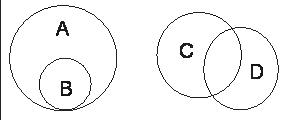
Рис.1
Рассмотрим наиболее важные свойства событий с помощью диаграмм Эйлера.
Объединением событий A и B называют событие C, состоящее из элементарных событий принадлежащих событию А или В (иногда объединения называют суммой).
![]()
Результат объединения можно изобразить графически диаграммой Эйлера (рис. 2).
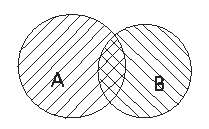
Рис.2
Пересечением событий А и В называют событие С, которое благоприятствует и событию А, и событию В (иногда пересечения называют произведением).
![]()
Результат пересечения можно изобразить графически диаграммой Эйлера (рис. 3).
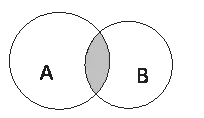
Рис.3
Если события А и В не имеют общих благоприятствующих элементарных событий, то они не могут наступить одновременно в ходе одного и то же опыта. Такие события называют несовместными, а их пересечение - пустое событие.
Разностью событий А и В называют событие С, состоящее из элементарных событий А, которые не являются элементарными событиями В.
![]()
Результат разности можно изобразить графически диаграммой Эйлера (рис.4)
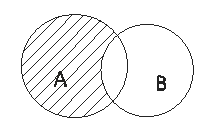
Рис.4
Пусть прямоугольник изображает все элементарные события. Событие А изобразим в виде круга внутри прямоугольника. Оставшаяся часть прямоугольника изображает противоположное событию ![]() A, событие
A, событие ![]() (рис.5)
(рис.5)
Событием, противоположным событию А называют событие, которому благоприятствуют все элементарные события, не благоприятствующие событию А.
Событие, противоположное событию А, принято обозначать ![]() .
.

Рис.5
Примеры противоположных событий.
- А - попадание при выстреле,
 - промах при выстреле;
- промах при выстреле; - В - выпадение герба при бросании монеты,
 - выпадение цифры при бросании монеты;
- выпадение цифры при бросании монеты; - С - безотказная работа всех элементов технической системы,
 - отказ хотя бы одного элемента;
- отказ хотя бы одного элемента; - D - обнаружение не менее двух бракованных изделий в контрольной партии;
 - обнаружение не более одного бракованного
изделия.
- обнаружение не более одного бракованного
изделия.
Объединением нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.
Например, если опыт состоит в пяти выстрелах по мишени и даны события:
А0- ни одного попадания;
А1- ровно одно попадание;
А2- ровно 2 попадания;
А3- ровно 3 попадания;
А4- ровно 4 попадания;
А5- ровно 5 попаданий.
Найти события: не более двух попаданий и не менее трёх попаданий.
Решение: А=А0+А1+А2 - не более двух попаданий;
В=А3+А4+А5 - не менее трёх попаданий.
Пересечением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Например, если по мишени производится три выстрела, и рассматриваются события:
В1 - промах при первом выстреле,
В2 - промах при втором выстреле,
ВЗ - промах при третьем выстреле,
то событие ![]() состоит в том, что в мишень не будет ни одного попадания.
состоит в том, что в мишень не будет ни одного попадания.
При определении вероятностей часто приходится представлять сложные события в виде комбинаций более простых событий, применяя и объединение, и пересечение событий.
Например, пусть по мишени производится три выстрела, и рассматриваются следующие элементарные события:
![]() - попадание при первом выстреле,
- попадание при первом выстреле,
![]() - промах при первом выстреле,
- промах при первом выстреле,
![]() - попадание при втором выстреле,
- попадание при втором выстреле,
![]() - промах при втором выстреле,
- промах при втором выстреле,
![]() - попадание при третьем выстреле,
- попадание при третьем выстреле,
![]() - промах при третьем выстреле.
- промах при третьем выстреле.
Рассмотрим более сложное событие В, состоящее в том, что в результате данных трёх выстрелов будет ровно одно попадание в мишень. Событие В можно представить в виде следующей комбинации элементарных событий:
![]()
Событие С, состоящее в том, что в мишень будет не менее двух попаданий, может быть представлено в виде:
![]()
На рис.6.1 и 6.2 показано объединение и пересечение трёх событий.

рис.6
Для определения вероятностей событий применяются не непосредственные прямые методы, а косвенные. Позволяющие по известным вероятностям одних событий определять вероятности других событий, с ними связанных. Применяя эти косвенные методы, мы всегда в той или иной форме пользуемся основными правилами теории вероятностей. Этих правил два: правило сложения вероятностей и правило умножения вероятностей.
Правило сложения вероятностей формулируется следующим образом.
Вероятность объединения двух несовместных событий равна сумме вероятностей этих событий:
Р(А+В) =Р(А)+ Р(В).
Сумма вероятностей противоположных событий равна единице:
Р(А) + Р(![]() )= 1.
)= 1.
На практике весьма часто оказывается легче вычислить вероятность противоположного события А, чем вероятность прямого события А. В этих случаях вычисляют Р (А) и находят
Р (А) = 1-Р(![]() ).
).
Рассмотрим несколько примеров на применение правила сложения.
Пример 1. В лотерее 1000 билетов; из них на один билет падает выигрыш 500 руб., на 10 билетов - выигрыши по 100 руб., на 50 билетов - выигрыши по 20 руб., на 100 - билетов - выигрыши по 5 руб., остальные билеты невыигрышные. Некто покупает один билет. Найти вероятность выиграть не менее 20 руб.
Решение. Рассмотрим события:
А - выиграть не менее 20 руб.,
А1 - выиграть 20 руб.,
А2 - выиграть 100 руб.,
А3 - выиграть 500 руб.
Очевидно, А= А1 +А2+А3.
По правилу сложения вероятностей:
Р (А) = Р (А1) + Р (А2) + Р (А3) = 0,050 + 0,010 + 0,001 = 0,061.
Пример 2. Производится бомбометание по трём складам боеприпасов, причём сбрасывается одна бомба. Вероятность попадания в первый склад 0,01; во второй 0,008; в третий 0,025. При попадании в один из складов взрываются все три. Найти вероятность того, что склады будут взорваны.
Решение. Рассмотрим события:
А - взрыв складов,
А1 - попадание в первый склад,
А2 - попадание во второй склад,
А3 - попадание в третий склад.
Очевидно, А = А1 + А2 + А3.
Так как при сбрасывании одной бомбы события Al, А2, А3 несовместны, то
Р (А) = Р (A1) + Р(А2) +Р(А3) == 0,01 + 0,008 + 0,025 = 0,043.
Пример 3. Круговая мишень состоит из трёх зон: I, II и III. Вероятность попадания в первую зону при одном выстреле 0,15, во вторую 0,23, в третью 0,17. Найти вероятность промаха.

Рис.7
Решение. Обозначим А - промах, ![]() - попадание.
- попадание.
Тогда ![]() =А1+ А2 + А3,
=А1+ А2 + А3,
где А1, А2 , А3 - попадание соответственно в первую, вторую и третью зоны:
Р(![]() ) = Р (A1) + Р (А2) + Р (А3) = 0,15 + 0,23 + 0,17 = 0,55,
) = Р (A1) + Р (А2) + Р (А3) = 0,15 + 0,23 + 0,17 = 0,55,
откуда
Р(А) = 1- Р(![]() ) = 0,45.
) = 0,45.