Урок-практикум по геометрии в 7-м классе "Свойства углов, образованных при пересечении параллельных прямых секущей"

Разделы: Математика

Цели урока: (Слайд №1)
Образовательные: закрепление умений использовать знания признаков, свойств углов, образованных при пересечении параллельных прямых секущей, научить видеть различные способы при решении одной задачи.
Воспитательные: воспитание познавательной активности, чувства ответственности, культуры общения.
Развивающие: развитие логического мышления учащихся, внимания, активности, чувство ответственности, самостоятельности, культуры общения.
Тип урока: урок обобщения и систематизации знаний учащихся.
Организационные формы: парная, дифференцированно групповая.
Технология: уровневая дифференциация.
Структура урока:

  • вводное слово учителя
  • самостоятельная работа групп №2, №3
  • актуализация знаний учащихся группы №1
    1. диктант
    2. тест
  • самостоятельная работа группы №1
  • защита у доски работ группами №2, №3

К данному уроку прилагается презентация (Приложение 1)

Ход урока:
Вводное слово учителя
Многие великие люди всех времен и народов говорили о значении математики. Не только ученые - математики, но и поэты, писатели, философы. Высказывание одного великого мыслителя: «ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства» Леонардо да Винчи (слайд №2).
Предметом исследования нашего урока будут углы, образованные при пересечении параллельных прямых секущей. Задачей нашего урока является обобщение и систематизация ваших знаний по данной теме.
В ходе групповой, парной, самопроверки вы еще раз закрепите знания свойств углов, образованных при пересечении параллельных прямых секущей (слайд №3).

Организация работы групп

  • класс делится на 3 группы по уровню их обученности
  • каждая группа получает определенные задания
  1. группа №3 - уровень «4-5». Решают по 3 задачи с последующей защитой у доски.
    Выполняют в тетрадях и сдают учителю.

    Задания для групп с уровнем обученности «4-5»

    Дано: a и b, c и d;
    <2 = 65°, <3 = 115°, <4 = 121°.
    Доказать: a || b
    Найти: <1
    В равнобедренных треугольниках ABC и DEF:
    <1 = <2
    Доказать: AB || CD
    На рисунке: MQ = NP
    <1 = <2
    Доказать: MN || PQ
  2. группа №2 - уровень на «4». Решают 4 задачи по готовым чертежам, по вариантам в парах с последующей защитой у доски, затем обмениваются вариантами и решают самостоятельно до конца урока. Выполняют в тетрадях и сдают учителю.

    Решение по готовым чертежам (задания для ребят с уровнем обученности «4»)

    Дано: a || b
    <1 больше <2 в 5 раз
    Найти: <1, <2, <3, <4
    Дано:m || n
    <2 + <8 = 100°
    Найти: остальные углы
    Дано: <1 = <2 = <3
    Доказать: a || b и m || n
    Дано: <8 = 83°
    <2 больше <1 на 14°
    Доказать: MN || AB
  3. группа №1 - с низким уровнем обученности. С этой группой начинает работать учитель.
    1. Диктант (слайды №4, №5, №6) - 7 мин. Выполняют на отдельных листах. Цель: проверить знания учащихся формулировки теорем, выражающих признаки параллельности прямых, свойств углов, образованных при пересечении секущей двух параллельных прямых, распознавать виды углов по рисунку.

      Диктант.
      Заполните пропуски в формулировке признаков, свойств углов при пересечении параллельных прямых секущей

      1. Две прямые на плоскости называются параллельными, если они…
      2. Если две параллельные прямые пересечены третьей, то сумма внутренних…
      3. Назовите на данном рисунке углы:
        1. внутренние накрестлежащие…
        2. соответственные…
        3. односторонние…
        4. смежные (две пары)…
        5. вертикальные (две пары)…
      4. Если один из внутренних накрестлежащих углов при параллельных прямых и секущей равен 34°
      5. Если две параллельные прямые пересечены третьей, то соответственные…
      6. Если один из односторонних углов при параллельных прямых и секущей равен 150°, то другой равен…
      7. Будут ли прямые параллельными, если односторонние углы равны по 30° и 120°

      Ответы к диктанту

      1. Две прямые на плоскости называются параллельными, если они не пересекаются.
      2. Если две параллельные прямые пересечены третьей, то сумма внутренних односторонних углов равна 180°
        1. 3 и 6; 4 и 5 – накрестлежащие
        2. 1 и 6; 2 и 5; 3 и 8; 4 и 7 – соответственные
        3. 3 и 5; 4 и 6 – односторонние
        4. 1 и 2; 2 и 3 – смежные
        5. 2 и 4; 1 и 3 – вертикальные
      4. 34°
      5. Углы равны
      6. 30°
      7. Нет, т.к. их сумма не равна 180°
    2. Самопроверка с обсуждением неверных ответов (слайд №7) - 5мин. Обмениваются ответами. После выполнения листы сдаются учителю.
    3. Тест (слайды №8, №9) - 8мин. Выполняют на отдельных листах Цель: проверить их умения объяснять по рисунку, какие углы являются накрест лежащими, соответственными, односторонними. Уметь применять признаки, свойства углов при решении задач (с учащимися работает ассистент-старшеклассник, а учитель работает с группой №2).

      Тест

      Выберите правильный ответ:
      1. Прямые a и b - параллельные, с-секущая. <7 и <1

      1. соответственные
      2. односторонние
      3. накрестлежащие

      2. Дано: <8 = 35°. Найти: <1

      1. не знаю
      2. <1 = 145°
      3. <1 = 35°

      3. Дано: m || n, <3 + <5 = 260°. Найти: <3

      1. <3 = 50°
      2. <3 = 130°
      3. не знаю

      4. Параллельны ли прямые a и b, если (см. рисунок)

      1. да
      2. не знаю
      3. нет


      Ответы к тесту:

      1. <7 и <1 (см. рис.)
        1. соответственные
        2. односторонние
        3. накрестлежащие
      2. <8 = 35°. Найти: <1
        1. не знаю
        2. 145°
        3. 35°
      3. m || n, <3 + <5 = 260°. Найти: <3
        1. <3 = 50°
        2. <3 = 130°
        3. не знаю
      4. Будет ли a и b, если (см. рис.)
        1. да
        2. не знаю
        3. нет
    4. самопроверка с обсуждением (слайды №10, №11) - 5 мин. После выполнения листы сдаются учителю.
    5. самостоятельная работа - 15мин. Выполняется в рабочих тетрадях, затем сдаются на проверку (в это время учитель работает с группой №3).

      Самостоятельная работа

      Вариант 1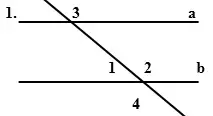
      Дано: a || b, c - секущая
      <3 = 138°
      Найти: <1, <2, <3
      Дано: p ? m, p ? n
      <2 = 40°, <7 = 40°
      Доказать : a || b
      Вариант 2
      Дано: m || n, p - секущая
      <1 = 34°
      Найти: <2, <3, <4
      Дано: c ? a, c ? b
      <8 = 120°, <1 = 60°
      Доказать : a || b