Урок алгебры в 8-м классе "Функция у=к:х и ее график"
ЦЕЛИ УРОКА:
Образовательная цель:
- научить строить график функции y= k/x опираясь на свойства функции;
- ввести понятие функции обратной пропорциональности;
- сформировать чёткое представление о различиях свойств и расположения графика функции при различных значениях k;
- расширить представления учащихся о функциях.
Развивающая цель:
- продолжить развитие познавательного интереса к изучению понятия функции;
- развивать умение анализировать, наблюдать, сопоставлять, логически мыслить;
- продолжить развитие элементов творческой деятельности учащихся , через вовлечение их в работу частично поискового характера, развитие навыков взаимоконтроля и самоконтроля.
Воспитывающая цель:
- воспитание навыков коммуникативности в работе, умение слушать и слышать другого, уважение к мнению товарища;
- воспитание у учащихся таких нравственных качеств, как настойчивость, аккуратность, инициативность, точность, привычка к систематичному труду, самостоятельность, активность;
- воспитание культуры общения.
Оборудование:
- интерактивная доска, проектор, компьютер; раздаточный материал для устного счета.
- Презентация к уроку.
ХОД УРОКА
I. Актуализация опорных знаний.
Учитель: Сегодня на уроке мы продолжаем знакомиться с новыми функциями, их свойствами и
графиком.
Чтобы определить учебные задачи нашего урока выполним следующую работу.
(У каждого ученика на парте раздаточный материал с заданием, необходимо
ответить на вопрос, найти верный ответ среди предложенных,
соответствующую букву записать в таблицу под правильным ответом).
- Дана функция f(x) = 5х2 - х. Найдите f(1).
- Найдите значение аргумента при котором значение функции у = 5х + 4 равно - 1.
- Найдите положительный нуль функции f(x) = x2 - 25.
- На рисунке изображен график функции у = f(x) на отрезке [- 3; 2].
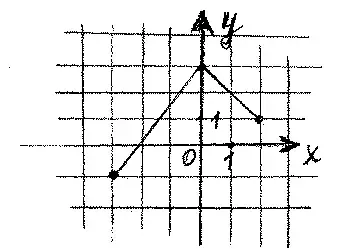
- Укажите наибольшее значение функции.
- Укажите промежуток в котором функция возрастает.
- Найдите промежуток в котором функция принимает отрицательные значения.
- Найдите нули функции.
- Найдите область значений функции.
- Найдите по графику f(2).
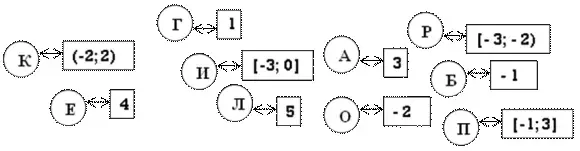
|
1 |
[-3; 0] |
[- 1; 3] |
4 |
[- 3; - 2) |
- 1 |
- 2 |
5 |
3 |
|
г |
и |
п |
е |
р |
б |
о |
л |
а |
II. Постановка проблемы.
Учитель: Какое слово получили? (Гипербола)
Что это за слово в математике?
Ученик выступает с сообщением: (это график некоторой функции. Одним из первых, кто начал изучать эту кривую был ученик знаменитого Платона, древнегреческий математик Менехм в IV в. до н.э., но так и не сумел её полностью изучить. А вот полностью исследовал свойства гиперболы и дал ей название крупнейший геометр древности Аполоний Пергский в III в. до н.э.).
Учитель: Сегодня мы с вами побываем в роли древнегреческих ученых.
Как вы думаете, какие задачи мы должны поставить и решить на уроке?
(Учащиеся пытаются сформулировать эти задачи с помощью учителя).
- Выяснить графиком какой функции является гипербола.
- Рассмотреть расположение графика функции в системе координат.
- Изучить свойства функции
III. Решение первой задачи.
"Какой формулой задается гипербола".
(Учитель читает задачи, учащиеся отвечают на вопросы, учащиеся записывают в тетради, один ученик на доске)
Задача № 1. Скорость пешехода V км/ч; t ч - время. Сколько времени потребуется пешеходу,
чтобы пройти 12 км. Выразить зависимость t от V.
Задача № 2. Площадь прямоугольника 60 кв. см. Одна сторона прямоугольника а см, другая
в см. Выразить зависимость в от а.
Задача № 3. Р руб. цена товара, m количество товара. Сколько товара можно купить на 500 руб?
Выразить зависимость m от Р.
Учитель: Как называются переменные a, v, p?
![]()
![]()
![]() Как называются переменные m, b, t?
Как называются переменные m, b, t?
Записать каждую зависимость в виде функции?
Что общего и в чем различие этих формул?
Составить функцию, которая является обобщением рассмотренных зависимостей
(Учащиеся с помощью учителя составляют формулу).
Определение.
Функция, заданная формулой ![]() где k
где k ![]() 0, называется обратной
пропорциональностью.
0, называется обратной
пропорциональностью.
Учитель: Детально рассмотрим эту зависимость с помощью графика на примере функции ![]() .
.
Как построить график незнакомой нам функции?
А как вы думаете, как будет называться график этой функции?
IV. Решение второй задачи.
"Построение графика функции".
- Составить таблицу значений (взять значения аргумента с расчетом, чтобы положение графика определялось с достаточной полнотой).
- Отметить точки на координатной плоскости.
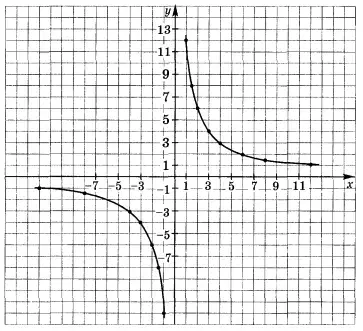
- Соединить точки линией.
(Все учащиеся строят в тетради, один ученик на доске)
Учитель: Давайте перечислим свойства этой функции.
(Учащиеся с помощью учителя перечисляют свойства построенной функции).
V. Решение третьей задачи.
Учитель: А как вы думаете, если мы возьмем отрицательное число k,
Что произойдет с расположением графика в системе координат?
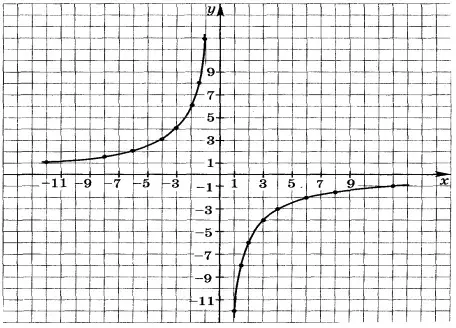
Исследовательская работа в парах.
Задание. Построить график функции![]() и описать свойства?
и описать свойства?
(Учащиеся выполняют задания в парах, после выполнения один из учеников записывает свойства на доске).
Учитель: Что произошло с графиком функции, при изменении коэффициента?
А теперь откроем учебники на стр. 225 и сравним полученный нами график с тем, что нам предлагает учебник?
VI. Первичное закрепление.
Самостоятельная работа обучающего характера.
I вариант. 1) № 781
2) В одной координатной плоскости постройте графики заданных функций и
найдите координаты их точек пересечения у = 2х - 2 и ![]() .
.
II вариант 1) № 780
2) В одной координатной плоскости постройте графики заданных функций и найдите координаты их точек пересечения у = х - 6 и ![]() .
.
Проверка. (Первое задание учитель проверяет у каждого проходя по рядам, второе задание на слайде заготовлено заранее)
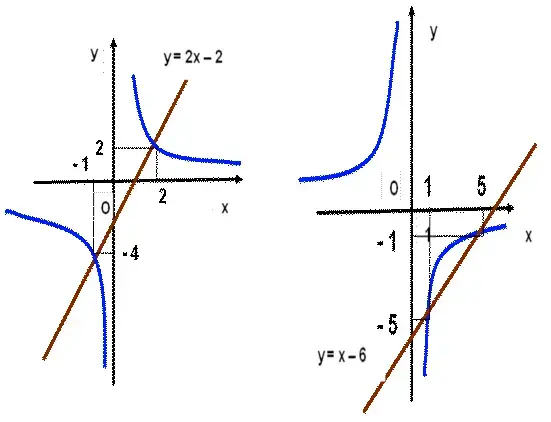
ИТОГ УРОКА.
- Что является графиком функции y=k/x.
- В каких координатных четвертях расположен график функции?
- Какова область определения функции
- Какими свойствами обладает график функции обратной пропорциональной зависимости?
- Из чего состоит гипербола?
(Устно).
1. Укажите какие из функций являются обратной пропорциональностью?
![]() ;
; ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ;
;
е) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
2. Перечислите свойства функции а) и в).
Задание на дом. П.5.6. № 783, № 784, 787 (б)
РЕФЛЕКСИЯ (каждому ученику выдан рисунок с изображением лица клоуна, необходимо дорисовать рот, используя следующие комментарии)

ГИПЕРБОЛА ВОКРУГ НАС (краткое выступление учащихся подготовленное заранее).
В явлениях природы, в человеческой деятельности часто встречаются обратно пропорциональные зависимости между двумя величинами. Гипербола может служить графиком любой такой зависимости. Астрономы всесторонне изучают строение космоса.
Среди тел Солнечной системы много комет. Вблизи Солнца многие кометы движутся по орбитам, близким к гиперболам.
Гипербола используется в строительном деле.
Фермы мостов делают так, что воображаемое продольное сечение их вертикальной плоскостью кривая линия, близка к гиперболе.
На свойство гиперболы обратили внимание поэты и писатели. Так в словаре русского языка Ожегова слово гипербола трактуется как поэтический приём чрезмерного преувеличения с целью усиления впечатления. Часто гипербола встречается в частушках:
Сидит лодырь у ворот
Широко разинув рот,
И никто не разберёт,
Где ворота, а где рот.
Русский поэт Н.А. Некрасов тоже любил этот прием и применял его в своих стихах. Например:
Пройдёт - словно солнцем осветит:
Посмотрит - рублём подарит!
… Я видывал, как она косит:
Что взмах - то готова копна.