Урок по теме "Решение дробных рациональных уравнений". 8-й класс

Игнатьева Светлана Михайловна, учитель математики

Разделы: Математика

Класс: 8

Цели урока:

Обучающая:

формирование понятия дробных рационального уравнения;
рассмотреть различные способы решения дробных рациональных уравнений;
рассмотреть алгоритм решения дробных рациональных уравнений, включающий условие равенства дроби нулю;
обучить решению дробных рациональных уравнений по алгоритму;
проверка уровня усвоения темы путем проведения тестовой работы.

Развивающая:

развитие умения правильно оперировать полученными знаниями, логически мыслить;
развитие интеллектуальных умений и мыслительных операций - анализ, синтез, сравнение и обобщение;
развитие инициативы, умения принимать решения, не останавливаться на достигнутом;
развитие критического мышления;
развитие навыков исследовательской работы.

Воспитывающая:

воспитание познавательного интереса к предмету;
воспитание самостоятельности при решении учебных задач;
воспитание воли и упорства для достижения конечных результатов.

Тип урока: урок – объяснение нового материала.

Ход урока

1. Организационный момент.

Здравствуйте, ребята! На доске написаны уравнения посмотрите на них внимательно. Все ли из этих уравнений вы сможете решить? Какие нет и почему?

Уравнения, в которых левая и правя часть, являются дробно-рациональными выражениями, называются дробные рациональные уравнения. Как вы думаете, что мы будем изучать сегодня на уроке? Сформулируйте тему урока. Итак, открываем тетради и записываем тему урока «Решение дробных рациональных уравнений».

2. Актуализация знаний. Фронтальный опрос, устная работа с классом.

А сейчас мы повторим основной теоретический материл, который понадобиться нам для изучения новой темы. Ответьте, пожалуйста, на следующие вопросы:

Что такое уравнение? (Равенство с переменной или переменными.)
Как называется уравнение №1? (Линейное.) Способ решения линейных уравнений. (Все с неизвестным перенести в левую часть уравнения, все числа - в правую. Привести подобные слагаемые. Найти неизвестный множитель).
Как называется уравнение №3? (Квадратное.) Способы решения квадратных уравнений. (Выделение полного квадрата, по формулам, используя теорему Виета и ее следствия.)
Что такое пропорция? (Равенство двух отношений.) Основное свойство пропорции. (Если пропорция верна, то произведение ее крайних членов равно произведению средних членов.)
Какие свойства используются при решении уравнений? (1. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному. 2. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.)
Когда дробь равна нулю? (Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.)

3. Объяснение нового материала.

Решить в тетрадях и на доске уравнение №2.

Решение:

9х = 18∙5

9х = 90

х = 90:9

х = 10

Ответ: 10.

Какое дробно-рациональное уравнение можно попробовать решить, используя основное свойство пропорции? (№5).

Решение:

(х-2)(х-4) = (х+2)(х+3)

х²-4х-2х+8 = х²+3х+2х+6

х²-6х-х²-5х = 6-8

-11х = -2

х = -2:(-11)

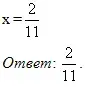
Решить в тетрадях и на доске уравнение №4.

Решение:

3х-3+4х = 5х

7х-5х = 3

2х = 3

х = 3:2

х = 1,5

Ответ: 1,5.

Какое дробно-рациональное уравнение можно попробовать решить, умножая обе части уравнения на знаменатель? (№6).

Решение:

12 = х(7-х)

12 = 7х-х²

х²-7х+12 = 0

D=1›0, х₁=3, х₂=4.

Ответ: 3;4.

Теперь попытайтесь решить уравнение №7 одним из способов.

Решение:

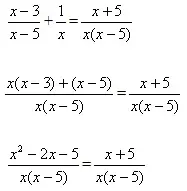
1 способ:			2 способ:
(х²-2х-5)х(х-5)=х(х-5)(х+5)
(х²-2х-5)х(х-5)-х(х-5)(х+5)=0			х²-2х-5=х+5
х(х-5)(х²-2х-5-(х+5))=0			х²-2х-5-х-5=0
х(х-5)(х²-3х-10)=0			х²-3х-10=0
х=0 х-5=0 х²-3х-10=0			D=49
х₁=0 х₂=5 D=49
х₃=5 х₄=-2			х₃=5 х₄=-2
Ответ: 0;5;-2.			Ответ: 5;-2.

Объясните, почему так получилось? Почему в одном случае три корня, в другом – два? Какие же числа являются корнями данного дробно-рационального уравнения?

До сих пор учащиеся с понятием посторонний корень не встречались, им действительно очень трудно понять, почему так получилось. Если в классе никто не может дать четкого объяснения этой ситуации, тогда учитель задает наводящие вопросы.

Чем отличаются уравнения № 2 и 4 от уравнений № 5,6,7? (В уравнениях № 2 и 4 в знаменателе числа, № 5-7 – выражения с переменной.)
Что такое корень уравнения? (Значение переменной, при котором уравнение обращается в верное равенство.)
Как выяснить является ли число корнем уравнения? (Сделать проверку.)

При выполнении проверки некоторые ученики замечают, что приходится делить на нуль. Они делают вывод, что числа 0 и 5 не являются корнями данного уравнения. Возникает вопрос: существует ли способ решения дробных рациональных уравнений, позволяющий исключить данную ошибку? Да, это способ основан на условие равенства дроби нулю.

Решение:

х²-3х-10=0 , D=49 , х₁=5 , х₂=-2.

Если х=5, то х(х-5)=0, значит 5- посторонний корень.

Если х=-2, то х(х-5)≠0.

Ответ: -2.

Давайте попробуем сформулировать алгоритм решения дробных рациональных уравнений данным способом. Дети сами формулируют алгоритм.

Алгоритм решения дробных рациональных уравнений:

Перенести все в левую часть.
Привести дроби к общему знаменателю.
Составить систему: дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
Решить уравнение.
Проверить неравенство, чтобы исключить посторонние корни.
Записать ответ.

Обсуждение: как оформить решение, если используется основное свойство пропорции и умножение обеих частей уравнения на общий знаменатель. (Дополнить решение: исключить из его корней те, которые обращают в нуль общий знаменатель).

4. Первичное осмысление нового материала.

Работа в парах. Учащиеся выбирают способ решения уравнения самостоятельно в зависимости от вида уравнения. Задания из учебника «Алгебра 8», Ю.Н. Макарычев,2007: № 600(б,в,и); № 601(а,д,ж). Учитель контролирует выполнение задания, отвечает на возникшие вопросы, оказывает помощь слабоуспевающим ученикам. Самопроверка: ответы записаны на доске.

№ 600

б) 2 – посторонний корень. Ответ:3.

в) 2 – посторонний корень. Ответ: 1,5.

№ 601

а) Ответ: -12,5.

ж) Ответ: 1;1,5.

5. Постановка домашнего задания.

Прочитать п.25 из учебника, разобрать примеры 1-3.
Выучить алгоритм решения дробных рациональных уравнений.
Решить в тетрадях № 600(а,г,д); №601(г,з).
Попробовать решить №696(а)(по желанию).

6. Выполнение контролирующего задания по изученной теме.

Работа выполняется на листочках.

Пример задания:

А) Какие из уравнений являются дробными рациональными?

Б) Дробь равна нулю, когда числитель ______________________ , а знаменатель _______________________ .

В) Является ли число -3 корнем уравнения №6?

Г) Решить уравнение №7.

Критерии оценивания задания:

«5» ставится, если ученик выполнил правильно более 90% задания.
«4» - 75%-89%
«3» - 50%-74%
«2» ставится учащемуся, выполнившему менее 50% задания.
Оценка 2 в журнал не ставится, 3 - по желанию.

7. Рефлексия.

На листочках с самостоятельной работой поставьте:

1 – если на уроке вам было интересно и понятно;
2 – интересно, но не понятно;
3 – не интересно, но понятно;
4 – не интересно, не понятно.

8. Подведение итогов урока.

Итак, сегодня на уроке мы с вами познакомились с дробными рациональными уравнениями, научились решать эти уравнения различными способами, проверили свои знания с помощью обучающей самостоятельной работы. Результаты самостоятельной работы вы узнаете на следующем уроке, дома у вас будет возможность закрепить полученные знания.

Какой метод решения дробных рациональных уравнений, по Вашему мнению, является более легким, доступным, рациональным? Не зависимо от метода решения дробных рациональных уравнений, о чем необходимо не забывать? В чем «коварство» дробных рациональных уравнений?

Всем спасибо, урок окончен.

6.02.2010