Метод неопределенных коэффициентов и его универсальность

Применение метода неопределённых коэффициентов основано на следующих двух теоремах.

Теорема №1 (о многочлене, тождественно равном нулю).

Если при произвольных значениях аргумента x значение многочлена f(x) = а₀+ а₁х + а₂х² +...+ а _nxⁿ, заданного в стандартном виде, равно нулю, то все его коэффициенты а₀, а₁, а₂, ..., а_n равны нулю.

Теорема №2 (следствие теоремы № 1).

Пусть и f(x) = а₀+а₁х +...+ а _nxⁿ, и g (x)= b ₀+ b ₁х + b ₂х² +...+ b_nxⁿ.
Для того чтобы f(x)= g(x)необходимо и достаточно, что бы а₀= b₀, а₁ = b₁, а₂ = b ₂ , ..., а _n= b_n
Рассмотрим примеры, иллюстрирующие использование метода неопределенных коэффициентов.

Деление многочлена на многочлен.

Пример 1. Выполнить деление многочлена х⁵ – 6х³ + 2х² -4 на многочлен х² – х + 1.

Решение: Надо найти такие многочлены Q(x) и R(x), что х⁵ – 6х³ + 2х² -4 = (х² – х + 1) Q(x) + R(x), причём степень многочлена R(x) меньше степени многочлена (х² – х + 1). Из того, что степень произведения многочленов равна сумме их степеней, следует, что степень многочлена Q(x) равна 5 – 2 = 3.

Многочлены Q(x) и R(x) имеют вид:

Q(x) = q ₃x³ + q ₂x² + q ₁x + q₀,
R(x) = r ₁x + r₀.
Подставим Q(x) и R(x): х⁵ – 6х³ + 2х² -4 = (х² – х + 1)( q ₃x³ + q ₂x² + q ₁x + q₀) + r ₁x + r₀.

Раскроем скобки в правой части равенства:

х⁵ – 6х³ + 2х² -4 =
= q ₃x ⁵ + q ₂x⁴ + q ₁x³ + q ₀x² – q ₃x⁴ - q ₂x³ - q ₁x² –q ₀ x + q ₃x³ + q ₂x² + q ₁x + q ₀ + r ₁x + r₀ =
= q ₃x ⁵ + (q₂ – q₃) x⁴ + (q₁ - q ₂ + q₃) x₃ + (q₀ - q ₁ + q₂) x² + (q₁ – q₀ +r₁) x + q₀ +r₀.

Для отыскания неизвестных коэффициентов получаем систему уравнений:

q₀ +r₀. = - 4, решая которую, получаем q₃ =1, q₂ =1, q₁ =-6,  q₀ =-5, r₁ = 1, r₀ = 1.

Ответ: Q(x) = x³ + x² - 6x - 5, R(x) = x + 1.

Пример 2. Выполнить деление многочлена х⁷ –1 на многочлен х³ + х + 1.

Решение: Надо найти такие многочлены Q(x) и R(x), что х⁷ –1 = (х³ + х + 1) Q(x) + R(x), причём степень многочлена R(x) меньше степени многочлена (х³ + х + 1).

Из того, что степень произведения многочленов равна сумме их степеней, следует, что степень многочлена Q(x) равна 7– 3 = 4.

Многочлены Q(x) и R(x) имеют вид: Q(x) = q ₄x⁴ + q ₃x³ + q ₂x² + q ₁x + q₀,
R(x) = r ₂x² + r ₁x + r0.

Подставим Q(x) и R(x):

х⁷ –1 = (х³ + х + 1) (q ₄x⁴ + q ₃x³ + q ₂x² + q ₁x + q₀ ) + ( r ₂x² + r ₁x + r₀ ).

Раскроем скобки в правой части равенства:

х⁷ –1= q ₄x ⁷ + q ₃x⁶ + q ₂x⁵ + q ₁x⁴ + q ₀x ³ + q ₄x⁵ + q ₃x⁴ + q ₂x³ + q ₁x² + q ₀ x +  q ₄x⁴ + q ₃x³ + q ₂x² +q ₁x + q ₀ + r ₂x² +r ₁x + r₀.
х⁷ –1= q ₄x ⁷ + q ₃x⁶+(q₂ + q₄) x⁵+(q₁+ q₃) x⁴+(q₀ + q ₂ + q₃) x³+(q₁ + q₂ +r₂) x² +(q₀ +r₁) x+( q₀ +r₀).

Получаем систему уравнений:

их которой получаем: q₄=1, q₃ = 0, q₂= -1, q₁ = -1, q₀ =1, r₂ = 2, r₁ =0 , r₀ = -2.

Ответ: Q(x) = x⁴ - x² - x + 1, R(x) = 2x² - 2.

Расположение многочлена по степеням.

Возьмем функцию Поставим перед собой задачу «расположить многочлен по степеням f(x) по степеням (х-х₀).

Задача сводится к нахождению неизвестных коэффициентов а₀, а₁, ..., а_n. В каждом конкретном случае эти числа найти легко. Действительно, расположим многочлены, находящиеся в левой и правой частях равенства, по степеням x. Так как мы имеем тождество, то (по теореме № 2) коэффициенты при одинаковых степенях x должны быть равны между собой. Приравняв коэффициенты правой части соответствующим заданным коэффициентам левой, мы придем к системе n+1 уравнений с n+1 неизвестными а₀, а₁, ..., а_n , которую нужно решить.

Пример 3. Расположим многочлен по степеням.

Решение. Полагаем:

Приравниваем коэффициенты при одинаковых степенях и получаем систему:

Решая систему, находим:

Ответ: .

Пример 4. Расположим f(x) = х⁴ - 8х³ + 24х² - 50х + 90 по степеням (х-2).

Решение: Полагаем х₄ - 8х³ + 24х² - 50х + 90 

Ответ: f(x) =

Представление произведения в виде многочлена стандартного вида.

Пример 5. Не выполняя действий, представим в виде многочлена стандартного вида произведение (х - 1)(х + 3)(х + 5).

Решение: Произведение есть многочлен третьей степени, коэффициент при старшем члене равен 1, а свободный член равен (- 15), тогда запишем:

(х - 1)(х + 3)(х + 5) = х³ + ах² + вх - 15, где а и в - неизвестные коэффициенты.

Для вычисления их положим х = 1 и х = - 3, тогда получим:

откуда а =7, в = 7.

Ответ: х³ +7х² + 7х - 15.

Разложение многочлена на множители

Пример 6. Дан многочлен

Разложим его на множители, если известно, сто все его корни – целые числа.

Решение: Будем искать разложение в виде:

полагая числа a, b, c и d его корнями. Раскроем скобки в правой части и сгруппируем по одинаковым степеням.

Приравниваем коэффициенты при одинаковых степенях.

Так как корни нашего многочлена – целые, то из последнего уравнения системы заключаем, что они должны быть делителями числа 30. Следовательно, их следует искать среди чисел

Проведя испытания, установим, что корни нашего многочлена -2, -5, 1 и 3. Следовательно х⁴+ 3х³ - 15х² - 19х + 30 = (х - 1)(х - 3)(х + 2)(х + 5)

Ответ: (х - 1)(х - 3)(х + 2)(х + 5)

Пример 7. Дан многочлен .

Разложим его на множители, если известно, сто все его корни – целые числа.

Решение: Будем искать разложение в виде:

 

полагая числа a, b, c и d его корнями. Раскроем скобки в правой части и сгруппируем по одинаковым степеням.

Приравниваем коэффициенты при одинаковых степенях.

Так как корни нашего многочлена – целые, то из последнего уравнения системы заключаем, что они должны быть делителями числа 84. Следовательно, их следует искать среди чисел

Проведя испытания, установим, что корни нашего многочлена -7,-2,2,3. Следовательно х⁴+ 4х³ - 25х² - 16х + 84 = (х - 2)(х - 3)(х + 2)(х + 7)

Ответ: (х - 2)(х - 3)(х +2)(х + 7)

Упрощение выражений

Пример 8. Разность является целым числом. Найдем это число.

Решение: Так как,

Тогда

Положим где a и b – неизвестные коэффициенты.

Тогда

Решая данную систему уравнений, получим а = 5, b = -4.

Значит так как

Аналогично устанавливаем, что

Следовательно

Ответ: -10

Пример 9. Является ли разность целым числом.

Решение: Т.к.

 тогда -  

Положим где a и b – неизвестные коэффициенты.

Тогда откуда

из второго уравнения тогда первое уравнение принимает вид

b² = 12,5 - - не удовлетворяет условию задачи, или b² = 9, откуда b = -3 или b = 3 - не удовлетворяет числу Значит, а = 5.

Аналогично,

Окончательно получаем: - иррациональное число.

Ответ: нет.

Уничтожение иррациональности в знаменателе

Пример 10. Избавимся от иррациональности в знаменателе:

Решение:

отсюда

Раскроем скобки, сгруппируем:

с = 4;
b - 4 = 1;
-а + 15 - 8 = 0;
b = 5;
а = 7

Ответ:

Пример 11. Избавимся от иррациональности в знаменателе:

Решение: ,

отсюда

Раскроем скобки, сгруппируем

Отсюда

Итак

Следовательно

Ответ:

Применение метода неопределенных коэффициентов при решении уравнений

Пример 12. Решим уравнение х⁴ + х³ - 4х² - 9х - 3 = 0.

Решение: Предположим, что корни уравнения - целые числа, тогда их надо искать среди чисел 

Если х = 1, то
если х = -1, то
если х = 3, то
если х = -3, то

Отсюда делаем вывод, что рациональных корней наше уравнение не имеет.

Попробуем разложить многочлен на множители в следующем виде:

, где a, b, c и d – целые. Раскроем скобки:

Приравнивая соответствующие коэффициенты выражений для неизвестных a, b, c и d получаем систему уравнений:

Так как bd = -3, то будем искать решения среди вариантов:

Проверим вариант № 2, когда b = -1; d = 3:

а = -2, с =3

Пример 13. Решить уравнение: х⁴ - 15х² + 12х + 5= 0.

Решение: Разложим многочлен f(х) = х⁴ - 15х² + 12х + 5 на множители в следующем виде: , где a, b, c и d -целые. Раскроем скобки:

Приравнивая соответствующие коэффициенты выражений для неизвестных a, b, c и d получаем систему уравнений:

Так как , bd = 5, то будем искать решения среди вариантов:

Системе удовлетворяет вариант №2, т.е. а = 3, b = -1, c = -3, d = 5.

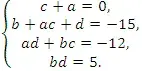
Итак,

D =13
D = 29

Ответ:

О решении одного класса кубических уравнений.

Пусть дано кубическое уравнение: а ₁ х³ + b ₁х² +с ₁х +d₁ = 0, где а ≠ 0. 
Приведём его к виду х³ + ах² +bх + с = 0 (1), где а = , в = , с =
Положим в уравнении (1) х = у + m. Тогда получим уравнение:
Раскроем скобки, сгруппируем:  y³+3у²m + 3ym² + m³ + ay²+ 2aym +am² + by +bm + с = 0,
y³ + y²(a +3m) +y(3m² +2am +b) + m³ +am² +bm + с = 0.

Для того, чтобы уравнение (1) было двучленным, должно выполняться условие:

Решения этой системы: m = -; a² = 3b. Таким образом, при произвольном с и при a² = 3b уравнение подстановкой х = у - можно привести к двучленному уравнению третьей степени.

Пример14. Решить уравнение: х ³ + 3х ²+3х - 9 =0.

Решение: В данном уравнении а = 3, в =3, тогда условие a² = 3b выполняется, а m = - = -1. Выполним подстановку х = у -1.

Уравнение принимает вид: (у -1)³ +3(у -1)² +3(у -1) – 9 = 0.
y³ -3y² +3у -1 +3у² – 6у +3 +3у –3 – 9 = 0.
y³ – 10 = 0, откуда у = , а х = - 1.

Ответ: - 1.

Пример15. Решить уравнение: х ³ + 6х ²+ 12х + 5 = 0.

Решение: а = 6, в =12, тогда условие a² = 3b (62 = 3×12) выполняется, а m = - = -2.

Выполним подстановку х = у - 2. Уравнение принимает вид: (у -2)³ +6(у -2)² +12(у -2) + 5 = 0.

у³ – 6у² + 12у – 8 + 6у² -24у + 24 + 12у – 24 + 5 = 0.
у³ – 3 = 0, у = , а х = - 2.

Ответ: – 2.

Рассмотренные в работе примеры могут быть решены и другими способами. Но цель работы заключалась в том, чтобы решить их методом неопределённых коэффициентов, показать универсальность этого метода, его оригинальность и рациональность, не отрицая того, что в некоторых случаях он приводит к громоздким, но не сложным преобразованиям.