Урок алгебры в 9-м классе по теме "Функция у=х^n, где n = 3, 4, 5. Её свойства и график"
Цель:
- Систематизировать и обобщить знания о функции и ее свойствах; расширить и углубить знания степенной функции с натуральным любым показателем.
- Формировать умения применять ранее полученные знания к умению использовать их в измененной ситуации, осознавать проблему, делать выводы, обобщать, развивать навыки самоконтроля и взаимоконтроля.
- Воспитывать умение общаться, вести диалог; волю для достижения поставленной цели; активность, целеустремленность.
Оборудование: интерактивная доска, проектор, ноутбук для демонстрации презентации.
Дидактический материал: Текст теста, раздаточный материал.
План урока:
- Организационный момент (проверить готовность учащихся к уроку необходимо за день или два до проведения урока)
- Повторение теоретических знаний (просмотр с комментированием презентаций основных теоретических вопросов темы)
- Теоретическое тестирование (проверка теоретических знаний по теме)
- Анализ допущенных ошибок при тестировании
- Постановка учебной задачи
- Решение поставленной задачи (работа в парах)
- Первичное закрепление изученного на уроке
- Проверка усвоения изученного на уроке (самостоятельная работа)
- Дача домашнего задания
- Подведение итогов
- Рефлексия
Ход урока
I. Организационный момент
Проверить готовность аппаратуры, наличие подготовленности учащихся к урокам, наличие необходимого материала на партах.
II. Повторение теоретических знаний
Комментарий учителя: После приветствия, постановки целей урока учитель предоставляет слово ученикам, которые заранее под руководством учителя готовили презентацию в которой систематизировали все, что было изучено в 7-8 классах по теме «Функции и их свойства». (см. приложение, слайд с 1 по 16 включительно)
III. Теоретический тест
Цель: проверить как усвоили учащиеся материал, представленный учащимися на слайдах.
1. Какой из графиков, изображенных на рисунке является функцией?
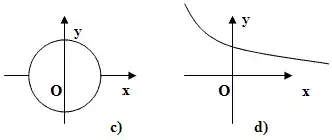
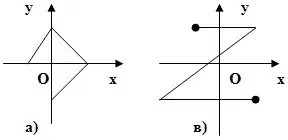
| 2. Область определения функции | равна… |
a) (-∞;3)∪(3; +∞)
b) (-∞; -3)∪(-3; 0)∪(0; +∞)
с) (-∞; 0)∪(0; +∞)
d) (-∞; +∞)
3. Какая из функций является четной?
a) у = х3 - 5х
b) у = х4 + 8х2
с) у = х2 + 2х
d) у = х3 - 1
4. Какая из функций, изображенных на рисунке является нечетной?
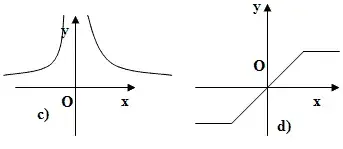
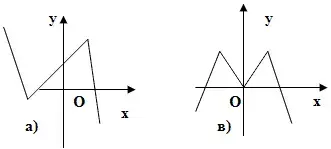
5. Наибольшее значение функции у = х2 на отрезке [-3; 0] равна…
a) 0
b) 6
с) 9
г) 3
6. Сколько среди заданных функций таких, которые ограничены сверху?
a) у = х
b) у = -х2 + 4
c) у = 1 / x
d) у = х2 + х
7. Какая из функций является возрастающей на отрезке [2; 50]?
a) у = -2х + 1
b) у = -х2 + 3
c) у = -3 / x
d) у = 5
8. В каких координатных четвертях расположен график функции у = ах2 + bх + с, если а > 0, D < 0?
а) 1 и 4
b) 1 и 2
c) 3 и 4
d) 1, 2, 3 и 4
9. График какой функции проходит через точку М(-4; -2)?
a) у = х2 - 1| b) |
d) у = - 2х + 1
| 10. Укажите область значений функции |
a)(- ∞; +∞)
b) [- 3; 3]
c) [0; +∞ )
d) [0; 3]
Проверка теста
Комментарии: (Осуществляется через самоконтроль)
После выполнения теста учащимся предоставляется ключ к ответам, после самопроверки каждый ученик выставляет себе оценку, отмечает вопросы, в которых затрудняется.
«5» - от 9 до 10 верных ответов
«4» - от 7 до 8 верных ответов
«3» - от 5 - 6 верных ответов
«2» - менее 5 верных ответов
Ключ к тесту
| Вопрос | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Ответ | d | b | b | d | с | b | с | b | с | d |
IV. Анализ теста
Комментарии: учащиеся задают вопросы в которых они испытывали трудности, учитель организует работу по решению возникших трудностей, привлекая к работе учащихся.
Для закрепления еще раз теории и вопросов по тесту, учащимся предлагается фронтальная работа, за правильный ответ ученику дается жетон, по окончании фронтального опроса и демонстрации ответов ученика, выставляются оценки ученикам, наиболее активно и правильно, отвечавшие на вопросы.
Задание
Используя график функции ответьте на вопросы:
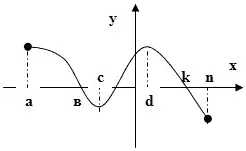
- Указать область определения функции
- Указать нули функции
- Четность, нечетность
- Промежутки монотонности
- Ограниченность
- Наибольшее, наименьшее значение
- Выпуклость, вогнутость функции
- Область значений функции
Комментарии: в это время более сильный ученик записывает ответы на эти же вопросы письменно на доске, работая самостоятельно, используя другой рисунок с указанием конкретных чисел.
После фронтальной работы ученикам демонстрируются ответы ученика, работающего самостоятельно у доски, обращается внимание учителя на часто допускаемые ошибки: скобки, знаки между промежутками.
V. Постановка учебной задачи
Учитель: -Как вы думаете, что является графиком функции у = х3 , у = х4, у = х5 и т. д.
Комментарии: учитель заслушивает ответы учеников и предлагает определить точно, что является графиком функции, выполнив задания в парах.
VI. Решение поставленной задачи (работа в парах)
I группа: для учащихся, сидящих на первом ряду.
Задание: на доске слайд из презентации, «исследование функции» (см. приложение, слайд 16)
Построить в одной системе координат графики функций: у = х2, у = х4; у = х6.
Записать свойства по алгоритму, сделать вывод относительно увеличения показателя степени.
Схематически расположить графики функции: у = -х2, у = -х4; у = -х6.
Прочитать устно свойства графика функции у = -хn, где n - четное натуральное число.
II группа: для учащихся, сидящих на втором ряду.
Задание: на доске слайд из презентации, «исследование функции» (см. приложение, слайд 16)
Построить в одной системе координат графики функций: у = х3, у = х5; у = х7.
Записать свойства по алгоритму, сделать вывод относительно увеличения показателя степени.
Схематически расположить графики функции: у = -х3, у = -х5; у = -х7.
Прочитать устно свойства графика функции у = -хn, где n - нечетное натуральное число.
Комментарии: пара, первая выполнившая работу каждого ряда, выходит к доске и записывает на доске решение, подробно объясняя по графику свойства. Учащиеся внимательно слушают и принимают участие в обсуждении, добавляют, исправляют, вносят коррективы. После корректировки и обсуждения, на доску выводятся слайды (№ 18 и № 19).
VII. Первичное закрепление темы
I шаг
Комментарий: Каждый ученик выполняет задание в тетради, трое учащихся у доски
Задание 1: Построить график функции у = (x + 2)6 и прочитать его устно.
Задание 2: Построить график функции у = х5 + 2 и прочитать его устно.
Задание 3: Построить график функции у = -(x + 4)4 - 1 и прочитать его устно.
Комментарий: После выполнения заданий учениками у доски, учащиеся проверяют решение, задают вопросы, которые у них возникли при решении.
II шаг
Комментарий: Каждый учащийся выполняет задание в тетради, один ученик комментирует с места, один ученик решает на закрытой доске тоже под диктовку этого ученика.
Задание: Решить графически уравнение х7 = х2 - 2.
Комментарий: Проверка осуществляется просмотром решения ученика работающего за закрытой доской. Учащиеся проводят самоанализ выполненной работы, задают вопросы в которых затруднялись при выполнении задания.
III шаг
Комментарий: Задания выполняются по вариантам. Двое учащихся (с каждого варианта) выполняют эти же задания самостоятельно у доски, учитель контролирует правильность выполнения, помогает по необходимости.
I вариант
Задание: Найдите наименьшее и наибольшее значения функции у = х6 - 1 на
а) отрезке [-1; 1],
б) на луче [1 / 2; +∞).
II вариант
Задание: Найдите наименьшее и наибольшее значения функции у = (х - 1)5 на
а) отрезке [-1; 1],
б) на луче [-2; +∞).
Комментарий: Проверка осуществляется путем взаимоконтроля, учащиеся меняются тетрадями и проверяют выполнение задания соседа, сверяя ее с решениями записанными на доске.
Комментарии: Для подведения итога этого этапа необходимо выполнить следующее задание.
Задание: Ученику было дано задание прочитать график функции
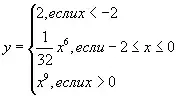
Верно ли ответил ученик?
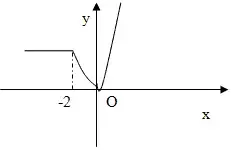
- D(f) = (-∞; +∞)
- Е(f) = (-∞; +∞)4
- Функция не является ни четной ни нечетной
- Возрастает: (-∞; 2]∪(0; +∞), убывает [-2; 0]
- Функция не ограничена ни сверху ни снизу
- Нет ни наименьшего значения ни наибольшего
- Функция непрерывна
- Выпукла вверх
Комментарии: Учащиеся дают анализ каждому ответу, если неправильно - дают теоретическое обоснование.
VIII. Проверка усвоения изученного на уроке (Проводится в виде самостоятельной работы, текст прилагается)
Вариант 1
- Постройте и прочитайте график функции:
а) у = х3 - 1;
б) у = -х4 + 6. - Определите число решений системы уравнений:
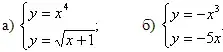
Вариант 2
- Постройте и прочитайте график функции:
а) у = (х + 2)4;
б) у = - х5. - Определите число решений системы уравнений:
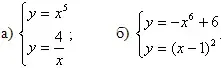
Комментарии: Учащиеся в течении 15 минут выполняют задания в тетради, решения записывают под копирку, тетради сдают учителю. Учитель предлагает проверить свои решения, сверив их с решениями, заранее записанными на доске учителем.
Учитель: - Какие трудности возникали при выполнении самостоятельной работы? (Учитель организует разбор данных вопросов)
IX. Домашнее задание
§11 № 314 (б), № 324
Дополнительно: № 327, повторить «Степень с отрицательным целым показателем».
X. Подведение итогов урока
Учитель:
- С графиками каких функций мы познакомились сегодня на уроке?
- Со свойствами какой функции, ранее нами изученной совпадают свойства функции у = х2n?
- Со свойствами какой функции, ранее нами изученной совпадают свойства функции у = х2n + 1?
- Что является графиком функции у = х21? Перечислите ее свойства. Приведите примеры функций, графики которых имеют аналогичные свойства.
- Что является графиком функции у = х48? Перечислите ее свойства. Приведите примеры функций, графики которых имеют аналогичные свойства.
- Что является графиком функции у = х-3?
(Учащиеся начинают предлагать свои варианты)
Учитель: Над этой функцией поработайте дома. Это тема следующего нашего урока.
XI. Рефлексия
Выбери для себя фигуру и определи (фигурки лежат на партах при выходе учащиеся их сдают учителю):
 |
Урок очень понравился, мне все было понятно |
| Урок вызвал интерес, я все вспомнил, что учили ранее, но есть вопросы, по которым нужна консультация | |
| Урок помог привести в систему знания, но дома некоторые задания самостоятельно выполнить не смогу | |
 |
Урок не понравился, нужна индивидуальная консультация |