Лабораторные работы на уроках геометрии

Белозерова Оксана Михайловна, учитель математики

Разделы: Математика

Лабораторная работа №1. (Приложение 1)

Тема: «Измерение отрезков».

Цели:

Проверить опытным путем, действительно ли длина отрезка равна сумме длин отрезков, на которые он делится точками;
Научиться решать задачи, используя свойство измерения отрезков.

Оборудование:

Линейка;
Карандаш;
Тетрадь;
Учебник.

Ход работы

1. Постройте отрезок АВ и отметьте на нём точку С так, как показано на рисунке.

2. Выполните измерения и заполните таблицу:

АС	СВ	АС + СВ	АВ

3. Постройте отрезок АВ и отметьте на нём точки С и D так, чтобы точка С лежала между точками А и D.

4. Выполните измерения и заполните таблицу:

АС	СД	ДВ	АС+СД+ДВ	АВ

5. Выводы:

Сделайте вывод о длине отрезка, если известны длины отрезков, на которые данный отрезок делится точками.

6. Решите задачу:

№ 1. На отрезке СД отмечена точка М. Найдите длину отрезка СД, если СМ=8см, а МД=11см.

Дано:

СД – отрезок

М є СД

СМ=8см, МД=11см

Найти: СД

Решение.

СД = СМ + МД (свойство измерения отрезков)

СД = 8 + 11 = 19 (см)

Ответ: СД = 19см

№ 2. На отрезке КС отмечены точки Д и А так, чтобы точка Д лежала между точками К и А.

Найдите длину отрезка КС, если КД=5см, ДА=9см, АС=7см?

Дано:

КС – отрезок

А є СД, Д є КА

КД=5см, ДА=9см

АС=7см

Найти: КС

Решение.

КС = КД + ДА + АС (свойство измерения отрезков)

КС = 5 + 9 + 7 = 21 (см)

Ответ: КС = 21см

№ 3. На отрезке АВ отмечена точка Д. Найдите длину отрезка АД, если АВ=18см, а ДВ=12см?

Дано:

АВ – отрезок

Д є АВ

АВ=18см, ДВ=12см

Найти: АД

Решение.

АД = АВ - ДВ (свойство измерения отрезков)

АД = 18 - 12 = 6 (см)

Ответ: АД = 6см

Контрольные вопросы:

В каких единицах измеряются отрезки?
Какими инструментами измеряются отрезки?
Как называется точка, делящая отрезок пополам?
Если отрезки равны, каковы их длины?
Как найти длину отрезка, если известны длины отрезков на которые данный отрезок делится точками?
Как найти часть отрезка, если известны длина всего отрезка и другой его части?

Все ответы вы можете найти в § 3-4; п. 6,7, 8 учебника.

Лабораторная работа №2. (Приложение 2)

Тема: «Измерение углов».

Цели:

Проверить опытным путем, действительно ли величина угла равна сумме градусных мер углов на которые делится данный угол лучами, исходящими из его вершины;
Научиться решать задачи, используя свойство измерения углов.

Оборудование:

Линейка;
Карандаш;
Тетрадь;
Учебник;
Транспортир.

Ход работы

1. Постройте угол АОВ и проведите из его вершины луч ОС.

2. Выполните измерения и заполните таблицу:

<АОС	<СОВ	<АОС+<СОВ	<АОВ

3. Постройте угол АОВ и проведите из его вершины лучи ОС и ОD, как показано на рисунке.

4. Выполните измерения и заполните таблицу:

<АОС	<СОД	<ДОВ	<АОС+<СОД+<ДОВ	<АОВ

5. Выводы:

Сделайте вывод о величине угла, если известны градусные меры углов, на которые данный угол делится лучами.

6. Решите задачу:

№ 1. Из вершины < АОВ проведен луч ОС так, что < АОС равен 34°, а < СОВ равен 27°. Найдите величину <АОВ.

Дано:

<АОВ, ОС – луч.

<СОВ=27°

Решение.

<АОВ = <АОС + <СОВ (свойство измерения углов)

<АОВ = 34° + 27° = 61°

Ответ: <АОВ = 61°

№ 2. Из вершины < КОД, равного 86°, проведен луч ОА так, что < КОА равен 37°. Найдите величину <АОД.

Дано:

<КОД =86°, ОС – луч

<КОА=37°

Найти: <АОД

Решение.

<АОД = <КОД - <КОА (свойство измерения углов)

<АОД = 86° - 37° = 49°

Ответ: <АОД = 49°

№ 3. Из вершины < АОВ, равного 84°, проведен луч ОС так, что < АОС в два раза меньше < СОВ. Найдите эти углы.

Дано:

<АОВ=84°, ОС – луч

<СОВ > <АОС в 2 раза

Найти: <АОС, <СОВ

Решение.

Пусть <АОС = х°, тогда <СОВ = 2х°. По условию задачи <АОВ = 84°. Используя свойство измерения углов, составим и решим уравнение: х + 2х = 84.

х + 2х = 84;

3х = 84;

х = 84: 3;

х = 28.

< АОС = 28°;

<СОВ = 2 · 28 = 56°

Ответ: < АОС = 28°; <СОВ = 56°

Контрольные вопросы:

В каких единицах измеряются углы?
Какими инструментами измеряются углы?
Если углы равны, каковы их величины?
Если луч делит угол пополам, как называется этот луч?
Какова величина прямого, острого, тупого, развернутого углов?
Как найти угол, если известны величины углов на которые делится угол лучами, исходящими из его вершины?
Как найти часть угла, если известна градусная мера всего угла и другой его части?

Все ответы вы можете найти в § 3,5; п. 6,9 учебника.

Лабораторная работа №3. (Приложение 3)

Тема: «Смежные углы».

Цели:

Проверить опытным путем, действительно ли сумма смежных углов равна 180°;
Научиться решать задачи, используя свойство смежных углов.

Оборудование:

Линейка;
Карандаш;
Тетрадь;
Учебник;
Транспортир.

Ход работы

1. Постройте два развернутых угла АОВ и проведите из его вершины луч ОС так, как показано на рисунках 1 и 2.

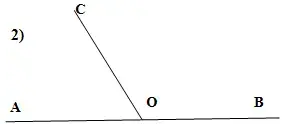
Выполните измерения и заполните таблицу:

№ опыта	<АОС	<СОВ	<АОС+<СОВ	<АОС
1
2

3. Выводы:

На основании проделанных опытов, сделайте вывод о сумме смежных углов.

4. Решите задачу:

№ 1. Один из смежных углов равен 34°. Найдите второй угол.

Дано:

<АОС и <СОВ - смежные

<СОВ=34°

Найти: <АОС

Решение.

<АОС = 180° - <СОВ (свойство смежных углов)

<АОС = 180° - 34° = 146°

Ответ: <АОС = 146°

№ 2. Найдите смежные углы <ас и <сb, если <ас в два раза больше <сb.

Дано:

<ас и <сb - смежные

<ас > <сb в 2 раза

Найти: <ас, <сb

Решение.

Пусть <сb = х°, тогда <ас = 2х°.

Используя свойство смежных углов, составим и решим уравнение: х + 2х = 180

х + 2х = 180;

3х = 180;

х = 180: 3;

х = 60.

<сb = 60°;

<ас = 2 · 60 = 120°

Ответ: < сb = 60°; <ас = 120°

Контрольные вопросы:

Какие углы называются смежными?
Сформулируйте свойство смежных углов.
Если один из смежных углов прямой (острый, тупой), каким является другой угол?
Верно ли утверждение: если смежные углы равны, то они прямые?
Даны два равных угла. Равны ли смежные с ним углы?

Все ответы вы можете найти в § 6; п. 11 учебника.

Лабораторная работа №4. (Приложение 4)

Тема: «Вертикальные углы»

Цель:

Проверить опытным путем, действительно ли действительно ли вертикальные углы равны

Оборудование:

Линейка;
Карандаш;
Тетрадь;
Учебник;
Транспортир.

Ход работы

1. Постройте вертикальные углы.

2. Выполните измерения и заполните таблицу:

№ опыта	<АОС	<ДОВ	Сравните <АОС и <ДОВ
1
№ опыта	<АОД	<ВОС	Сравните <АОД и <ВОС
2

3. Выводы:

Сравните вертикальные углы и сделайте вывод об их величине.

Контрольные вопросы:

Какие углы называют вертикальными?
Каким свойством обладают вертикальные углы?
Какой не может быть величина вертикальных углов?
Может ли сумма вертикальных углов равняться 120°? 280°? Если да, то чему равен каждый угол?
Может ли разность вертикальных углов равняться 28°? 0°? Почему?

Все ответы вы можете найти в § 6; п. 11 учебника.

Лабораторная работа №5. (Приложение 5)

Тема: «Равнобедренный треугольник. Свойство углов равнобедренного треугольника».

Цели:

Проверить опытным путем, действительно ли углы при основании равнобедренного треугольника равны;
Действительно ли высота, проведенная к основанию равнобедренного треугольника, является биссектрисой и медианой.

Оборудование:

Линейка;
Карандаш;
Тетрадь;
Учебник;
Транспортир.

Ход работы

1. Постройте два различных равнобедренных треугольника АВС с основанием АС.

2. Выполните измерения углов при основании равнобедренного треугольника и заполните таблицу:

№ опыта	<А	<С	Сравните <А и <С
1
2

3. Постройте равнобедренный треугольник АВС и проведите высоту ВД к основанию АС.

4. Выполните измерения и заполните таблицу:

АД	СД	Сравните АД и СД

<АВД	<СВД	Сравните углы <АВД и <СВД

5. Выводы:

Сделайте вывод о величине углов при основании равнобедренного треугольника (таблица 1);
Чем является высота, проведенная к основанию равнобедренного треугольника (таблица 2).

Контрольные вопросы:

Какой треугольник называется равнобедренным?
Что называется биссектрисой, медианой и высотой треугольника?
Каким свойством обладают медианы, высоты и биссектрисы треугольника?
Свойство углов при основании равнобедренного треугольника?
Свойство высоты, медианы и биссектрисы, проведенных к основанию равнобедренного треугольника?

Все ответы вы можете найти в Гл. 2 § 2; п. 16-18 учебника.

20.03.2008