Курс предпрофильной подготовки учащихся 9-х классов "Элементы теории множеств"
Пояснительная записка
Программа данного элективного курса рассчитана на 9 часов. Подобранный материал способствует расширению объема сведений по математике, а также обучению подростков навыкам анализа нестандартных ситуаций, самостоятельной работе с литературой, развитию математической речи.
В настоящее время большинство разделов математики построены на базе теоретико-множественных идей. Использование множеств и операций над ними позволяет осветить с современных позиций целый ряд разделов школьной математики. В то же время основные понятия теории множеств настолько просты и ясны, что их можно начинать преподавать с начальной школы.
При проведении занятий по теории множеств большое внимание уделяется разбору примеров множеств из окружающего мира. Надо научить школьников видеть конкретные примеры множеств, подмножеств, пересечений и объединений множеств и т.д. В то же время следует разобрать достаточное число примеров из уже известных школьникам вопросов математики, научить подходить к этим вопросам с теоретико-множественных позиций. Такие понятия, как система уравнений и неравенств, совокупность уравнений и неравенств, получают естественное истолкование на языке теории множеств.
Цель курса: познакомить учащихся с элементами теории множества.
Задачи курса:
- познакомить учащихся с понятием множества;
- познакомить учащихся с основными операциями: объединение и пересечение множеств;
- дать определение подмножества;
- рассмотреть конечные, бесконечные, числовые множества;
- рассмотреть число элементов объединения и пересечения двух конечных множеств;
- предоставить учащимся возможность, проанализировать свои способности к математике.
Распределение часов
|
№ |
Тема занятия |
Кол-во часов |
Виды деятельности учащихся |
| 1. | Понятие множества. Элемент множества. Пустое множество. |
1 |
Составление конспекта. Коллективное решение задач. Работа со справочной литературой. |
| 2. | Понятие подмножества. |
1 |
Деятельность учащихся направлена на выработку умения, отличать множества от подмножества. |
| 3. | Пересечение и объединение множеств. |
1 |
Выполнение тренировочных упражнений на отработку определений пересечения и объединения множеств. Проводятся тренировочные упражнения в устной форме на применение терминов из теории с целью развития математической речи. |
| 4. | Конечные и бесконечные множества. |
1 |
Используя навыки определения множества и подмножества, учащиеся самостоятельно
пытаются дать определение конечному и бесконечному множеству. Приводят примеры из жизненного опыта, рассматривают упражнения в письменной и устной форме. |
| 5. | Число элементов объединения и пересечения двух конечных множеств |
1 |
На конкретных примерах учащиеся самостоятельно формулируют свойства, записывают их в тетрадь. Выполняют тренировочные упражнения, которые помогают закрепить полученные знания. |
| 6. | Числовые множества. Числовые промежутки. |
1 |
Деятельность учащихся направлена на выработку умения, правильно записывать числовые промежутки. Упражнения выполняются в письменной форме. |
| 7. | Взаимно однозначное соответствие между множествами. |
1 |
Конспект лекции, работа со справочной литературой. Отработка полученного материала с записью в тетради. |
| 8. | Разность множеств. |
1 |
Составление опорного конспекта, оформление рисунков на доске, сообщение учеников по данной теме. |
| 9. | Проверочная работа. |
1 |
Обобщение знаний и проверка с помощью выполнения письменной работы составленной по аналогии с пройденным материалом. |
Дидактический материал
Тема 1. Понятие множества. Элемент множества. Пустое множество
Цель: ввести понятие множества, его элементов.
Справочный материал
В повседневной жизни постоянно различные совокупности предметов называют, одним словом. Совокупность документов называют архивом; собрание музыкантов - оркестром; группу лошадей - табуном; родителей, детей и их родственников - семьей; большую группу людей - толпой или очередью; собрание книг - библиотекой и т.д.
Математическим понятием, отражающим объединение некоторых объектов, предметов или понятий в одну единую совокупность является понятие множества. Это понятие не определяется, подобно понятиям точки, числа, и является первичным.
Предметы (объекты), составляющие некоторое множество, называются его элементами. Все множества можно записывать с помощью заглавных букв латинского алфавита:
А - множество квадратов;
В - множество чисел.
Элементы множества можно записать с помощью маленьких букв: х является элементом множества А. Это можно записать так: х![]() А (читают: х есть элемент
множества А, или х принадлежит А, или х содержится в А, или А содержит х). Если объект х не является элементом множества А, то это записывают так: х
А (читают: х есть элемент
множества А, или х принадлежит А, или х содержится в А, или А содержит х). Если объект х не является элементом множества А, то это записывают так: х![]() А
(читается: х не есть элемент множества А, или х не принадлежит А, или х не содержится в А).
А
(читается: х не есть элемент множества А, или х не принадлежит А, или х не содержится в А).
Например: Если множество В - множество натуральных чисел, то 2![]() В, -7
В, -7![]() В, муха
В, муха![]() В и т.д.
В и т.д.
Множество можно иногда задавать перечислением его элементов. Например: множество стран на земном шаре задается их списком в географическом атласе, множество учеников в классе - их списком в классном журнале. Если множество задано списком, то названия всех элементов множества записывают в фигурные скобки, разделяя запятой. Например: если множество С состоит из трех элементов:1,9 и -4, то это записывают так: С ={1,9; -4}.
Но не все множества можно записывать списком. Если множество содержит бесконечно много элементов, то такой список составить нельзя. Множество считается заданным, если указано некоторое свойство, которым обладают все его элементы и не обладают ни какие другие объекты. Такое свойство называют характеристическим свойством множества. Например: множество {2, 4} может быть задано:
а)множество четных чисел, удовлетворяющих неравенству 1 < х < 5;
б)множество корней квадратного уравнения х2 - 6х + 8 = 0.
Задание множества его характеристическим свойством записывают и в геометрии. Например: биссектриса угла есть геометрическое место точек плоскости, лежащих внутри этого угла и равноудаленных от его сторон.
Множество элементов обладающих характеристическим свойством записывают так:
А = {х: -3 < х < 4} означает, что множество А состоит из всех чисел х, удовлетворяющих неравенству -3 < х < 4.
Упражнения
№ 1. Как называется множество артистов, работающих в одном театре?
№ 2. Как называется множество царей данной страны, принадлежащих одному семейству?
№ 3. Пусть А множество всех многочленов от одной переменной х, все коэффициенты которых целые.
Верна ли запись:
а) х - 15 х + 6![]() А;
А;
б) ![]() х3 - 1
х3 - 1![]() А;
А;
в) х2 + у2 - 1![]() А.
А.
№ 4. На координатной плоскости расположен квадрат АВСД, где А(10; 10), В(-10; 10), С(-10; -10), Д(10, -10). Сколько точек с целыми координатами, расположено на сторонах квадрата или внутри его?
Дома
№ 1. Запишите известные вам названия множеств военнослужащих.
№ 2. На координатной плоскости расположен треугольник АВС, где А(-3; -2), В(0; 8), С(10; -5). Сколько точек с целыми координатами, расположено на сторонах треугольника или внутри его?
Тема 2. Понятие подмножества
Цель: ввести понятие подмножества, его элементов.
Справочный материал.
При помощи операций над множествами можно получать новые множества. Рассмотрим операцию пересечение множеств.
Пересечение множеств А и В есть множество, которое состоит из элементов, принадлежащих каждому из множеств А и В.
Обозначается операция пересечения: А![]() В.
В.
Например: А = {1; 2; 3}и В ={2; 3; 4; 5}, то А![]() В = {2; 3}.
В = {2; 3}.
Наглядно представить расположение множеств в различных случаях можно при помощи геометрических фигур.
![]()
Множества называются не пересекающимися, если у них нет общих элементов, т. е. их пересечение пусто.
Если заданы два множества, то можно образовать новое множество, включив в него, во-первых, элементы первого множества и, во-вторых, элементы второго множества, не совпадающие с элементами первого. Рассмотрим операцию объединение множеств.
Объединение множеств А и В представляет собой множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В. Обозначается операция объединения: А![]() В.
В.
Например: А = {1; 2; 3}, В = {2; 3; 4}, то А ![]() B = {1; 2; 3; 4}.
B = {1; 2; 3; 4}.
Упражнения.
№ 1. На координатной плоскости даны три множества:
- А - множество точек А(х; у), у которых | x | = 1;
- В - множество точек В(х; у), таких, что | y | = 1;
- С - множество, равное графику функции у = 2х.
Изобразите множества:
a) A
B;
б) АВ;
в) АС;
г) ВС;
д) АВ
С
№ 2.Назовите 5 подмножеств в множестве слов русского языка.
№ 3. Каким свойством выделяется подмножество млекопитающих в множестве всех живых существ?
Дома.
Пусть А - множество четных чисел из промежутка [100;1000], а В - множество чисел, кратных 5, из того же промежутка.
Сколько чисел в множестве: а) A ![]() B; б) А
B; б) А ![]() В
В
Тема 3. Пересечение и объединение множеств.
Цель: ввести понятия пересечения и объединения множеств.
Справочный материал.
Если каждый элемент множества В является в то же время элементом множества А, то говорят, что В -> подмножество в А, и пишут
В![]() А. Каждое непустое множество имеет по крайней мере два подмножества: пустое множество
А. Каждое непустое множество имеет по крайней мере два подмножества: пустое множество ![]() и само множество А. Таким образом, пустое множество является подмножеством любого множества.
и само множество А. Таким образом, пустое множество является подмножеством любого множества.
Упражнения.
№ 1. Даны множества:
а) Множество А всех тетрадей.
б) Множество В всех прямоугольников.
в) Множество С всех четырехугольников.
г) Множество D всех квадратов.
д) Множество Е всех параллелограммов.
е) Множество F всех многоугольников.
Выписать буквы, обозначающие эти множества, в таком порядке, чтобы каждая следующая обозначала подмножество предыдущего.
№ 2. Даны множества:
а) Множество А всех рациональных чисел.
б) Множество В всех целых чисел.
в) Множество С всех действительных чисел.
г) Множество D всех четных натуральных чисел.
д) Множество Е всех натуральных чисел.
е) Множество F всех натуральных чисел, делящихся на 12.
Выписать буквы, обозначающие эти множества, в таком порядке, чтобы каждая следующая обозначала подмножество предыдущего.
№ 3. Даны множества:
а) Множество А учеников 8-го класса данной средней школы.
б) Множество В всех учеников данной средней школы.
в) Множество С учеников 8-го класса этой средней школы, посещающие факультативные занятия по математики.
г) Множество Е всех учащихся средней школы в России.
д) Множество D всех учащихся средних школ города Салехард.
е) Множество F мальчиков из 8 класса, посещающих факультативные занятия по математике.
Выписать буквы, обозначающие эти множества, в таком порядке, чтобы каждая следующая обозначала подмножество предыдущего.
Дома.
Даны множества:
а) Множество А всех позвоночных животных.
б) Множество В всех животных.
в) Множество С всех млекопитающих животных.
г) Множество D всех волков.
д) Множество Е всех хищных млекопитающих.
Выписать буквы, обозначающие эти множества, в таком порядке, чтобы каждая следующая обозначала подмножество предыдущего.
Тема 4. Конечные и бесконечные множества.
Цель: ввести понятие конечного и бесконечного множества, научить оперировать этими понятиями при решении задач.
Справочный материал.
Множество, элементы которого можно пересчитать называется конечным множеством. Конечное множество можно задавать двумя способами:
- указанием на некоторое свойство, которому удовлетворяют его элементы;
- перечислением его элементов.
Например: А = {х: -3 < х < 4} означает, что множество А состоит из всех чисел х, удовлетворяющих неравенству -3 < х < 4.
Пустое множество считается конечным.
Свойство: Подмножество конечного множества само конечно.
Множество, элементы которого невозможно пересчитать называется бесконечным.
Свойство: Если множество В содержит бесконечное подмножество, то В бесконечно.
Упражнения
№ 1. Пусть конечное множество А содержит n элементов. Подсчитать, сколько подмножеств имеет это множество.
№ 2. Угадай по какому закону составлено бесконечное множество, содержащие числа:
а {![]() ,
,![]() ,
,![]() ,
,![]() ,…};
,…};
б) {![]() ,
,![]() ,
,![]() ,
,![]() ,…}
,…}
в) {![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…}
,…}
г) {2, 12, 36, 80, 150,…}
№ 3. Как называется множество точек земной поверхности, равноудаленных от северного полюса?
№ 4. Пусть Е - множество, состоящее из таких чисел х, что 4 < х2 < 9. Проверьте, что [2; 3]![]() Е. Верно ли, что [2; 3] = Е?
Е. Верно ли, что [2; 3] = Е?
Дома.
№ 1. На координатной плоскости расположен квадрат АВСД, где А(10;10), В(-10;10), С(-10;-10), Д(10;-10). Сколько точек с целыми координатами, расположено на сторонах квадрата или внутри его?
№ 2. Как называется множество точек земной поверхности, равноудаленных от обоих полюсов? Поясните ответ.
Тема 5. Число элементов объединения и пересечения двух конечных множеств
Цель: определить число элементов объединения и пересечения двух конечных множеств.
Справочный материал.
Нам уже известно, что пересечением двух не пустых множеств является новое множество, состоящее из элементов принадлежащих каждому из множеств. Если говорить о двух конечных множествах, то можно заметить, что их пересечение есть тоже конечное множество, состоящее из элементов принадлежащих каждому из множеств. Можно сказать и об объединении двух конечных множеств, оно тоже конечно.
Упражнения
№ 1. Пусть А - множество корней квадратного уравнения: х2 - 7х + 12 = 0.
- Верна ли запись - 5
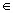 А?
А? - Верна ли запись 10
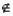 А?
А? - Верна ли запись 4
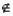 А?
А?
Составьте список элементов множества А.
№ 2. Пусть А - множество делителей числа 60.
- Верна ли запись 7
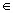 А?
А? - Верна ли запись 10
 А?
А? - Верна ли запись 20
 А?
А?
Составьте список элементов множества А.
№ 3. Составьте список элементов множества, заданных свойствами:
а) А = {х : х2 - 8х + 12 = 0};
б) В = {х : х![]() N, -11 < х < -3}.
N, -11 < х < -3}.
№ 4. Запишите с помощью фигурных скобок множество, состоящее из:
а) целы чисел, таких, что -3,71 < х < 4;
б) натуральных делителей числа 124 числа 30;
Дома.
№ 1. Запиши с помощью фигурных скобок множество корней уравнения:
а) 5х - 17 = 3;
б) (х - 1)(х - 2) = 0;
в) х2 + 9 = 0.
№ 2. В следующих множествах все элементы, кроме одного, обладают некоторым свойством. Найдите элементы не обладающие этим свойством:
а) {2; 6; 15; 84; 156};
б) {2; 7; 13; 16; 29}
Ответ поясните.
№ 3. Назовите отличия записи множества А = {2; 4} от множества [2; 4].
Тема 6. Числовые множества. Числовые промежутки.
Цель: ввести понятие "числовые промежутки" и "числовые множества", учить применять на практике.
Справочный материал.
Некоторые числовые множества имеют особые названия. Если даны два числа а и b, а < b, то множество всех чисел, удовлетворяющих неравенству, а < х < b, называют числовым отрезком и обозначают [а; b]. На числовой оси ему соответствует отрезок с концами а и b.
![]()
а b
Множество чисел, удовлетворяющих неравенству, а < х < b, называют числовым промежутком и обозначают (а, b). На числовой оси это множество изображается отрезном у которого отброшены концы.
Иногда встречаются множества чисел, удовлетворяющие неравенствам, а < х < b или а < х < b. Их называют числовыми полуотрезками и обозначают [а; b), или (а; b]. Квадратная скобка обозначает, что соответствующий конец включается в множество, а круглая - что он исключается.
Числовые отрезки, полуотрезки и промежутки имеют конечную длину. Рассмотрим множество чисел, удовлетворяющих неравенству а < х < +![]() . Такое множество называется числовым лучом. Числовой луч имеет бесконечную длину. Числовыми лучами называют и множества чисел, удовлетворяющих
неравенствам вида а < х < +
. Такое множество называется числовым лучом. Числовой луч имеет бесконечную длину. Числовыми лучами называют и множества чисел, удовлетворяющих
неравенствам вида а < х < +![]() , -
, - ![]() < х <
а, -
< х <
а, - ![]() < х < а числовые лучи обозначают так: [а; +
< х < а числовые лучи обозначают так: [а; +![]() ), (а;
+
), (а;
+![]() ), (-
), (- ![]() ; а], (-
; а], (- ![]() ; а). С числовыми множествами
приходится иметь дело при решении уравнений и неравенств.
; а). С числовыми множествами
приходится иметь дело при решении уравнений и неравенств.
Упражнения.
№ 1. Найдите область допустимых значений (ОДЗ) уравнения:
. ![]()
№ 2.Найдите ОДЗ для уравнений:
а)![]() ;
;
б) х2 + 5х + 7 + ![]() = 1 +
= 1 + ![]() .
.
№ 3. Совпадают ли ОДЗ уравнений: х + 5 = 15 - х и х + 5 +![]() .
.
Дома.
№ 1. Найдите ОДЗ для уравнений: ![]() .
.
№ 2. Придумайте и запишите элементы множества, используя рисунок.
А) 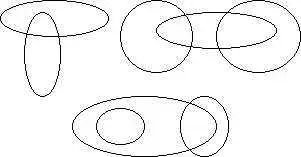 Б)
Б)
В)
Тема 7. Взаимнооднозначное соответствие между множествами
Цель: ввести понятие взаимного однозначного соответствия между множествами.
Справочный материал.
Между множествами А и В установлено взаимно-однозначное соответствие, если каждому элементу а из А поставлен в соответствие b из В, и при этом соответствии каждый элемент b из В соответствует одному и только одному элементу а из А.
Например: в случае, когда на танцевальной площадке танцуют все, между множеством юношей и множеством девушек устанавливается соответствие, обладающее следующими свойствами:
1) Каждому юноше соответствует одна и только одна девушка - его партнерша.
2) Каждой девушке соответствует один и только один юноша - ее партнер.
Понятие взаимнооднозначное соответствие весьма важное при изучении функции. Рассмотрим функцию: у = ![]() . Когда х изменяется на отрезке
[-1; 2], то у изменяется на отрезке [-1; 8]. При этом каждому числу х из отрезка [-1; 2] соответствует одно и только одно значение у, принадлежащее отрезку[-1;8], а каждому значению у из отрезка [-1;
8] - одно и только одно значение х из отрезка [-1; 2]. Иными словами, функция у =
. Когда х изменяется на отрезке
[-1; 2], то у изменяется на отрезке [-1; 8]. При этом каждому числу х из отрезка [-1; 2] соответствует одно и только одно значение у, принадлежащее отрезку[-1;8], а каждому значению у из отрезка [-1;
8] - одно и только одно значение х из отрезка [-1; 2]. Иными словами, функция у =![]() устанавливает взаимнооднозначное соответствие между точками отрезков [-1;
8] и [-[1; 2]. Эта функция устанавливает и взаимно однозначное соответствие между точками числовых прямых х и у. Отсюда следует, что каждому значению у соответствует единственное значение х, такое,
что х
устанавливает взаимнооднозначное соответствие между точками отрезков [-1;
8] и [-[1; 2]. Эта функция устанавливает и взаимно однозначное соответствие между точками числовых прямых х и у. Отсюда следует, что каждому значению у соответствует единственное значение х, такое,
что х![]() = у.
= у.
Упражнения.
№ 1. Приведите пример функции, которая не задает взаимно однозначного соответствия. Ответ объясните.
№ 2. Каждой параболе, ось которой параллельна оси ординат, ставится в соответствие ее уравнение вида у = а![]() +
bх + с. Является ли это соответствие взаимно однозначным?
+
bх + с. Является ли это соответствие взаимно однозначным?
№ 3. Пусть А - множество всех окружностей на плоскости и В - множество всех квадратов плоскости. Каждому квадрату ставят в соответствие вписанную в него окружность. Является ли это соответствие взаимно однозначным?
№ 4. Пусть А - множество всех окружностей на плоскости и В - множество всех точек этой плоскости. Каждой окружности ставится в соответствие ее центр. Является ли это соответствие взаимно однозначным?
№ 5. Найдите объединение корней уравнений (3х + 5) + (8х + 1) = 17 и 2х = 20.
Дома.
№ 1. Каждому квадратному уравнению вида ![]() (а и b - положительные числа) ставится в соответствие его
положительный корень. Является ли это соответствие взаимно однозначным?
(а и b - положительные числа) ставится в соответствие его
положительный корень. Является ли это соответствие взаимно однозначным?
№ 2. Найдите пересечение двух прямых у = х и у = 2- х. Ответ запишите в виде множества состоящего из элементов.
Тема 8. Разность множеств
Цель: ввести понятие разности множеств и научить применять его на практике.
Справочный материал.
Разностью двух множеств А и В называется такое множество, в которое входят все элементы из множества А, не принадлежащие множеству В.
Разность множеств А и В обозначают А\В. Если рассмотреть разность множеств А и В с помощью диаграмм Эйлера-Вена, то видим А\В = ![]() когда А
= В.
когда А
= В.
В случае, когда В - есть подмножество множества А, разность А\В называют дополнением множества В в множестве А и обозначают САВ*.

Например, дополнением множества четных чисел в множестве всех целых чисел является множество нечетных чисел. Дополнением множества всех квадратов в множестве прямоугольников является множество всех прямоугольников с неравными сторонами. Разность множеств используется при решении уравнений с переменными в знаменателе.
Упражнения.
№ 1. Что представляет собой множество:
а) САА;
б) СА ![]() ?
?
№ 2. Пусть А = [1; 4], В = [2; 6]. Найдите множества А\В и В\А. Чему равно множество (А\В)![]() (В\А)?
(В\А)?
Найдите дополнение множества правильных треугольников в множестве всех треугольников; всех правильных многоугольников.
Дома.
Пусть А = {х/х = 2м - 1, м - целое число}, В = {х/х = 4к + 1, к - целое число}. Опишите множество А\В.
Тема 9. Проверочная работа
Цель: проверить знания и умения, учащихся по элементам теории множеств.
Справочный материал.
ВАРИАНТ 1.
№ 1. Даны множества:
А = {12; 4; 2; 78}, В = {15; 3; 24; 5}, С = {15; 3; 5; 21; 76}.
Найдите:
а) А ![]() В; б) А
В; б) А ![]() В; в) В
В; в) В ![]() С; г) А
С; г) А ![]() С; д) В
С; д) В ![]()
![]() .
.
№ 2.Пусть А - множество делителей числа 80.
- Верна ли запись 7
 А?
А? - Верна ли запись 10
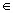 А?
А? - Верна ли запись 20
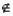 А?
А? - Составьте список элементов множества А.
№ 3. Даны множества:
а) Множество В всех прямоугольников;
б) Множество С всех четырехугольников;
в) Множество D всех квадратов;
г) Множество Е всех параллелограммов;
д) Множество F всех многоугольников.
Выписать буквы, обозначающие эти множества, в таком порядке, чтобы каждая следующая обозначала подмножество предыдущего.
№ 4.. На координатной плоскости расположен треугольник АВС,
где А(0; 8), В(2; -4), С(-6; -2). Сколько точек с целыми координатами, расположено на сторонах треугольника или внутри его?
№ 5.Найдите пересечение двух прямых у = 3х и у = х + 2. Ответ запишите в виде множества состоящего из элементов.
№ 6.Запиши с помощью фигурных скобок множество корней уравнения:
а) 2х -17 = 3;
б) (х - 4)(х - 3) = 0;
в) х2 + 16 = 0.
№ 7.Пусть Е - множество, состоящее из таких чисел х, что 9 = х2 = 25.
Проверьте, что [3; 5]![]() Е. Верно ли, что [3; 5] = Е?
Е. Верно ли, что [3; 5] = Е?
№ 8. Найдите ОДЗ для уравнений: а)![]() .
.
ВАРИАНТ 2.
№ 1. Даны множества: А = {1; 5; 7; 13}, В = {15; 3; 7; 23}, С = {17; 23; 2; 15; 3}.
Найдите:
а) А ![]() В; б) А
В; б) А ![]() В; в) В
В; в) В ![]() С; г) А
С; г) А ![]() С; д) В
С; д) В ![]()
![]() .
.
№ 2. Пусть А - множество делителей числа 60.
- Верна ли запись 7
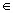 А?
А? - Верна ли запись 10
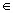 А?
А? - Верна ли запись 20
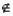 А?
А? - Составьте список элементов множества А.
№ 3. Даны множества:
а) Множество А всех рациональных чисел.
б) Множество В всех целых чисел.
в) Множество С всех действительных чисел.
г) Множество D всех четных натуральных чисел.
д) Множество Е всех натуральных чисел.
е) Множество F всех натуральных чисел, делящихся на 12.
Выписать буквы, обозначающие эти множества, в таком порядке, чтобы каждая следующая обозначала подмножество предыдущего.
№ 4. На координатной плоскости расположен треугольник АВС, где А(3; 1), В(-2; -8), С(-4; 7). Сколько точек с целыми координатами, расположено на сторонах треугольника или внутри его?
№ 5. Найдите пересечение двух прямых у = х и у = 2 - х. Ответ запишите в виде множества состоящего из элементов.
№ 6. Запиши с помощью фигурных скобок множество корней уравнения:
а) 5х - 17 = 3;
б) (х - 1)(х - 2) = 0;
в) х2 + 9 = 0.
№ 7. Пусть Е - множество, состоящее из таких чисел х, что 4 = х2 = 9. Проверьте, что [2; 3]![]() Е. Верно ли, что
[2; 3] = Е?
Е. Верно ли, что
[2; 3] = Е?
№ 8. Найдите ОДЗ для уравнений: а)![]() .
.
Дополнительные упражнения.
№ 1. Каждая семья, живущая в нашем доме, выписывает или газету, или журнал, или то и другое вместе. 75 семей выписывают газету, а 27 семей выписывают журнал и лишь 13 семей выписывают и журнал, и газету. Сколько семей живет в нашем доме?
№ 2. Из 40 учащихся нашего класса 32 любят молоко, 21 - лимонад, а 15 - и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
№ 3.В одном классе 25 учеников. Из них 7 любят груши, 11 - черешню. Двое любят груши и черешню; 6 - груши и яблоки; 5 - яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?
№ 4.Из 100 человек 85 знают английский язык, 80 - испанский, 75 - немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя иностранными языками. Сколько человек из этих 100 знают 3 языка?
![]()
№ 5. Учитель задал на уроке сложную задачу. В результате количество мальчиков, решавших задачу, оказалось равно количеству девочек, ее не решивших. Кого в классе больше - решивших задачу или девочек?
№ 6. Сколько человек участвовало в прогулке, если известно, что 16 из них взяли с собой бутерброды с ветчиной, 24 - с колбасой, 15 - с сыром, 11 - с ветчиной и с колбасой, 8 - с ветчиной и с сыром, 12 - с колбасой и с сыром, 6 - бутерброды всех трех видов, а 5 - вместо бутербродов взяли с собой пирожки?
Литература:
- И.Л. Никольская. "Факультативный курс по математике", учебное пособие для 7-9-х классов средней школы. М., "Просвещение", 1991.
- К.П. Сикорский. "Дополнительные главы по курсу математики 7-8 классов для факультативных занятий", М., "Просвещение", 1969.
- Н.А. Виленкин. "Алгебра" учебник для учащихся 8 класса с углубленным изучением математики, М., "Просвещение", 2005.
- И.Н. Бронштейн, К.А. Семендяев. "Справочник по математике для инженеров и учащихся ", М., "Наука", 1986.
- А.Г.Ципкин. "Справочник по математике", для средних учебных заведений, М., "Наука", 1988.