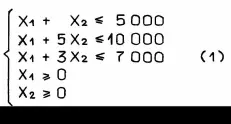Интегративные элективные курсы для профильных классов
Как известно, с 2005-2006 учебного года в России начался переход на профильное обучение в старших классах общеобразовательных школ. Поэтому при ведении уроков и элективных курсов мне открывается широкое поле для реализации своего педагогического кредо: недостаточно только дать знания, важно научить их применять.
В рамках данной статьи приведены фрагменты элективных курсов по математике с учащимися микробиологического класса, экономического класса и класса математиков-программистов, а также приведены программы элективных курсов для учащихся 10 классов указанных профилей, рассчитанные на 10 часов каждая.
1. Начнем с рассмотрения одного занятия с учащимися микробиологического класса.
На уроках биологии учащимися изучалась тема "Дигибридное скрещивание. Второй закон Менделя" из раздела "Основы генетики и селекции". На примере двух нетрудных задач из данного раздела биологии [1] я смог разобрать с ребятами такие математические разделы, как "Бином Ньютона. Треугольник Паскаля", "Основы комбинаторики. Введение в теорию вероятностей".
Задача 1: "В какой пропорции пойдет расщепление признаков во втором поколении (F2), если первый родитель (Р1) - доминантная тетрогомозигота, а второй родитель (Р2) - рецессивная тетрогомозигота?".
Краткая запись условия выглядит так:
Дано:
Р1 : АА ВВ СС DD
Р2 : аа bb cc dd
Найти: F2 -?
Решение (с точки зрения биологии):
F2 = (3:1)4
Ответ: F2 = 81:27:27:27:27:9:9:9:9:9:9:3:3:3:3:1
Обоснование (с точки зрения математики):
Такая принятая в биологии запись, как 3:1, означает, что число всех комбинаций признаков равно 4, т.е. математически эта запись означает 3+1 (3 случая одного признака и 1 случай другого признака из возможных 4 случаев)
Когда мы имеем пару признаков АА и аа, то выполняется первый закон Менделя, т.е. F2 = 3:1 (четверть особей несет рецессивный признак, три четверти - доминантный). Таким образом, число всех возможных комбинаций признаков равно 4.
Когда мы добавили к рассмотрению еще одну пару признаков (BB и bb), то число всех возможных комбинаций стало равно 4*4 = 16.
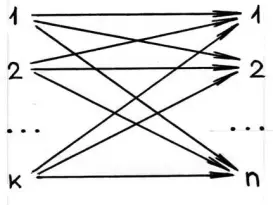
В самом деле, если к n объектам добавить еще k объектов, то число всех возможных комбинаций по 2 объекта- один из первой группы, один из второй - равно n * k. Это можно представить в виде схемы (рис. 1):
рис. 1
Эта схема может служить наглядной иллюстрацией при объяснении материала "Правило умножения" в разделе "Элементы комбинаторики".
Таким образом, при наличии 4 пар признаков получается, что общее число комбинаций равно 4*4*4*4 = 256.
Возвращаясь к записи (3:1)n, скажем, что ее математическим эквивалентом будет выражение (3+1)n . Эта запись может означать и число всевозможных пар, о чем говорилось выше, и пропорциональность распределения наследования признаков. Последний факт может быть проиллюстрирован с помощью "треугольника Паскаля".
(a+b)n = an +Сn 1 an-1 b + … + Сn n-1 a bn-1 + bn ( * )
Коэффициенты перед слагаемыми будут указывать вероятность появления определенных наборов признаков. Помочь определить эти коэффициенты способен "треугольник Паскаля":
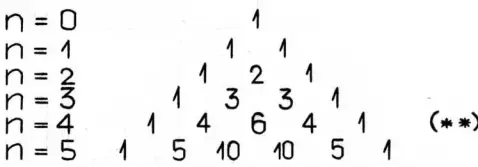
В результате, пользуясь (*), (**), имеем: (3:1)4 = 81: 27:27:27:27:9:9:9:9:9:9:3:3:3:3:1
Задача 2: "В какой пропорции и в каком поколении пойдет расщепление признаков, если первый родитель (Р1) - по 1 и 3 признаку доминантная гомозигота, а по 2 и 4 признаку - гетерозигота; при этом второй родитель (Р2) - по 2, 3 и 4 признаку - рецессивная гомозигота, а по 1 признаку - гетерозигота?".
Краткая запись условия выглядит так:
Дано:
Р1 : АА Вb СС Dd
Р2 : Аа bb сс dd
Найти: F -?
Решение:
Рассмотрим АА х Аа:
получается АА, АА и Аа, Аа. Будем исходить из того, что и первых пар, и вторых пар достаточно много (так как законы генетики носят статистический характер). Для определенности будем считать, что их по 1 000 000. Чтобы получить аа, необходимо сначала "взять" Аа. Это можно сделать с вероятностью, равной 1/2. Далее необходимо "взять" снова Аа. Так как мы считаем, что число пар достаточно велико, то можно считать, что пар Аа осталось не 499 999, а, по-прежнему, 500 000. Таким образом, вторую пару Аа можно "вытащить" с вероятностью, равной 1/2. Итак, поскольку события, заключающиеся в двойном последовательном случайном "вынимании" пар Аа, то по правилу умножения вероятностей "вытащить" две пары Аа можно с вероятностью, равной 1/4.
Так как при скрещивании Аа и Аа признак аа может проявиться в одном из 4 случаев, то общая вероятность появления аа равна 1/4 * 1/4 = 1/16, т.е. пропорция выглядит как 15:1.
Рассмотрим Вb x bb: признак bb получается в первом поколении в 2 случаях из 4, т.е. с вероятностью 1/2 или в пропорции 1:1.
Рассмотрим СС х сс: признак сс может проявиться лишь во втором поколении (т.к. в первом все признаки будут доминантными) в одном случае из 4, т.е. в пропорции 3:1.
Наконец, рассмотрим Dd x dd: аналогично уже рассмотренному случаю имеем проявление признака dd в первом поколении в пропорции 1:1.
Таким образом, имеем:
- F2 : 15:1
- F1 : 1:1
- F2 : 3:1
- F1 : 1:1
Схематично этот ответ можно изобразить следующим образом (рис. 2):
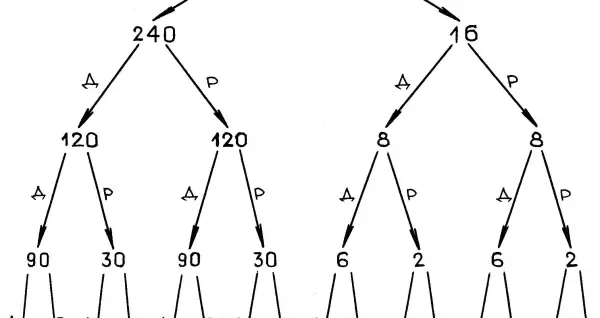
рис. 2
Таким образом, пропорция выглядит следующим образом:
45:45:15:15:45:45:15:15:3:3:1:1:3:3:1:1, а каждый признак возможно проследить по цепочке на схеме.
2. Теперь перейдем к рассмотрению задания, предлагавшегося на занятии с учащимися класса математиков-программистов. На предыдущих занятиях мы затронули вопросы математического моделирования: формализация задачи, ее решение и интерпретация ответа.
На отчетном занятии учащимся была предложена проблема: "Рассчитать необходимое количество касс в некоем универсаме" [3].
Первый этап перевода условия задачи на математический язык и построения математической модели был преодолен совместно учителем и учащимися:
Дано:
k - необходимое количество касс;
t - время обслуживания кассиром одного покупателя;
T - время работы магазина;
n - количество покупателей, побывавших в магазине за день.
В течение рабочего дня один кассир может обслужить T/t покупателей. Следовательно, число касс надо взять таким, чтобы они смогли обслужить всех покупателей, побывавших в магазине за день. Итак, математическая модель этой задачи: k = n : (T/t).
Далее учащимся были представлены данные, необходимые для решения поставленной задачи, т.е. ребята узнали время обслуживания одного покупателя кассиром, число покупателей, посетивших магазин за день:
t = 2мин; T = 12 ч = 720 мин; n = 540 человек.
Таким образом, имеем : k = 540 : (720/2) = 1,5.
На этапе интерпретации делаем вывод: чтобы не создавалось очереди в магазине должно работать не менее 2 касс (k =1,5).
При анализе данной ситуации учащиеся пришли к выводу, что посетители магазина приходили не равномерно: днем их было мало, а вечером произошел их наплыв. Поэтому днем один кассир мог быть не занят, а вечером у двух касс могли скапливаться очереди. Так ребята сделали вывод о том, что построенная модель была слишком упрощена и не отвечала практическим требованиям. Чтобы сделать модель более достоверной, мы стали считать не общее число покупателей, а рассчитывать необходимое количество касс в каждый час работы магазина. Была построена новая модель:
k i = ni : (1/t), где k i - число касс, необходимое в i-й час работы магазина; ni - число покупателей в i-й час работы магазина.
Ответом будет служить k = max ki .
3. Опишем теперь работу учащихся экономического класса на одном из занятий элективного курса по математике:
учащимся предлагалась следующая задача: "Ферма занимается возделыванием только двух культур - зерновых и картофеля - и располагает следующими ресурсами: пашня - 5 000 га, труд - 300 000 чел.-час, возможный объем тракторных работ - 28 000 условных га. Найти оптимальное сочетание посевных площадей культур" [2].
Для составления математической модели учащимся была предложена таблица с нормативами затрат и выхода продукции для данной фермы:
| Культуры | Затраты на 1 га посева | Стоимость валовой продукции с 1 га, р. | |
| Труда, чел.-час | Тракторных работ, усл. га | ||
|
Зерновые
Картофель |
30
150 |
4
12 |
400
1000 |
Критерием оптимальности является максимум стоимости валовой продукции. Этот максимум должен достигаться в условиях использования ограниченных ресурсов пашни, труда и механизированных работ. В задаче имеется множество допустимых вариантов сочетания посевных площадей двух культур, но не все из них равнозначны с точки зрения требования оптимальности.
Для поиска оптимального решения задачи обозначим через х1 га площадь, отводимую под зерновые, а через х2 га - площадь, отводимую под картофель. Тогда стоимость зерновых составит 400 х1 р., а стоимость картофеля - 1000 х2 р. Отсюда стоимость всей валовой продукции составит (400 х1 + 1000 х2) p. Обозначим это выражение через у:
у = 400 х1 + 1000 х2
Нам надо найти максимум этой целевой функции при соблюдении следующих условий:
а) общая площадь зерновых и картофеля не должна превышать 5000 га, т. е. х1+x2<5000;
б) общие затраты труда не должны превосходить 300 тыс. человеко-часов, т. е.
30 х1 +150х2 < 300 000 (или х1 +5х2 < 10 000);
в) общий объем механизированных работ не должен превосходить 28 000 усл. га,
т. е. 4 х1 + 12х2<28 000 (или х1 + 3х2<7 000);
г) площади, отводимые под зерновые и картофель, могут принимать только неотрицательные значения: х1 ?0; х2?0
Таким образом, условия задачи выражаются следующей системой неравенств:
Требуется найти такие значения х1 и х2,при которых функция у = 400 х1 + 1000 х2 принимает наибольшее значение.
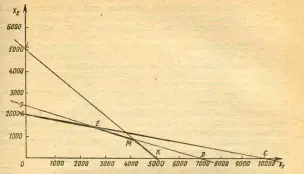
Решение задачи было выполнено графическим способом: на координатной плоскости Х1 0 Х2 были построены прямые х1 + х2 = 5000, х1 + 5х2 = 10000,
х1 + 3х2 = 7000 (рис. 3).
Рис. 3
Затем была выделена область, состоящая из точек плоскости, координаты которых удовлетворяют системе (1). Этой областью являлся пятиугольник (рис. 4).
рис. 4
Для нахождения наибольшего значения функции у = 400 х1 + 1000 х2 были найдены ее значения в вершинах пятиугольника. Наибольшее значение функции было при х1 = 4000, х2 = 1000.
Таким образом, оптимальное сочетание посевных площадей культур: зерновые - 4000 га, картофель - 1000 га.
На конечном этапе решения задачи был проведен экономический анализ оптимального ее решения.
При х1 =4000 и х2 =1000:
х1 + х2 = 5000, а это значит, что пашня используется полностью.
4х1 + 12х2 = 4*4000 + 12*1000 = 28 000. Это означает, что ресурсы тракторного парка используются полностью.
30х1 + 150х2 = 30*4000 + 150*1000 = 270 000. Это значит, что трудовые ресурсы недоиспользованы на 30000 чел.-ч. Полное использование трудовых ресурсов сдерживается ограниченностью пашни и мощностью тракторного парка.
Таким образом, для рассмотренной в задаче фермы ресурсы имеют разную ценность: человеческих рук в избытке, а механизированный труд дефицитен.
В заключение статьи приведем программы элективных курсов по математике для учащихся 10 класса, рассчитанных на 10 часов:
математического профиля:
- Этапы решения любой задачи. Понятие модели задачи.
- Постановка задачи. Выделение существенных свойств.
- Переформулировка задачи. Переход от одной модели задачи к другой. Оптимизация решения задачи.
- Решение задач из области физики.
- Решение задач "на сложные проценты" из области экономики.
- Решение комбинаторных задач.
- Решение "жизненных" задач (данное занятие рассмотрено в статье).
- Решение задач. Подготовка к контрольной работе.
- Контрольная работа: "Решение задач с практическим содержанием".
- Анализ контрольной работы.
экономического профиля:
- Этапы решения любой задачи. Понятие модели задачи.
- Постановка задачи. Выделение существенных свойств.
- Переформулировка задачи. Переход от одной модели задачи к другой.
- Решение задач "на сложные проценты".
- Решение задач из области управления предприятием.
- Решение комбинаторных задач
- Оптимизация решения задачи (данное занятие рассмотрено в статье).
- Решение задач. Подготовка к контрольной работе.
- Контрольная работа: "Решение задач с практическим содержанием".
- Анализ контрольной работы.
микробиологического профиля:
- Этапы решения любой задачи. Понятие модели задачи.
- Постановка задачи. Выделение существенных свойств.
- Переформулировка задачи. Переход от одной модели задачи к другой.
- Решение задач по теме "Генетика". Бином Ньютона. Треугольник Паскаля (данное занятие рассмотрено в статье).
- Решение задач по теме "Генетика". Элементы комбинаторики. Введение в теорию вероятностей (данное занятие рассмотрено в статье).
- Решение комбинаторных задач.
- Решение вероятностных задач.
- Решение задач. Подготовка к контрольной работе.
- Контрольная работа: "Решение задач с практическим содержанием".
- Анализ контрольной работы.
В данной статье автором была описана часть собственной работы на элективных курсах по математике с учащимися 10 классов различных профилей. Главная цель, преследуемая нами, заключается в интеграции математики и других учебных предметов, а также в постановке акцента на применении знаний, на их практическом использовании, что является важным условием для формирования компетентностей у выпускников школы.
ЛИТЕРАТУРА:
- Беляев Д. К., А.О. Рувинский и др. Общая биология. Учебник для 10-11 классов средней школы. М., 1993
- Шапиро И.М. Использование задач с практическим содержанием в преподавании математики. М., 1990
- Шульга Е.В. Сколько нужно касс в нашем универсаме//Математика в школе, № 5, 2001.