“Недостаточно только дать знания, важно научить их применять”
Педагогическое кредо автора статьи.
В рамках данной статьи рассматриваются 2 урока в 10 классе экономического профиля по алгебре и началам анализа. Уроки предполагают групповую форму работы и проводятся в форме викторин.
Цели проведения викторин:
образовательная:
- способствовать систематизации знаний по темам “Логарифмы”; “Логарифмическая функция”; “Логарифмические уравнения и неравенства”;
развивающие:
- способствовать формированию умений у учащихся применять теоретические знания при решении практических заданий по математике
- способствовать развитию у учащихся навыков логических рассуждений
- способствовать развитию у учащихся умения моделировать;
воспитательные:
- способствовать формированию и развитию:
- навыков критического отношения к проделанной работе
- чувства ответственности за работу коллектива
- умений и навыков работы в группе
- навыков участия в общем диалоге
- умений выдерживать конкуренцию
- положительного микроклимата в классе.
Оборудование: учащиеся объединены в группы, каждой группе учащихся выданы листы в клетку для оформления решений и черновиков. На партах должны быть канцелярские принадлежности, лист бумаги с номером группы (выбран жребием) и полным составом группы, с указанием капитана, в каждой группе должны быть часы. Для наглядности ответов должны быть доска и цветной и белый мел (или маркеры).
Далее рассмотрим ход двух уроков.
Урок-викторина: “Логарифмические уравнения и неравенства”Организационный момент.
Вступительное слово учителя о том, что класс разделяется на 4 группы и по сказанным дальше правилам участвует в викторине по теме “Логарифмические уравнения и неравенства”. Также учитель доводит до ребят цели урока: систематизировать знания по темам “Логарифмы”; “Логарифмическая функция”; “Логарифмические уравнения и неравенства”, развить умения применять знания при решении практических задач, а также развить умения работы в группах, где успех коллектива зависит от действий каждого из его участников.
Первый этап. Погружение.
Командам формулируется следующее задание (для погружения в игру): придумать название своей команды, девиз, выбрать капитана. На это отводится 4 минуты придумать и по 1 минуте озвучить. Учитель записывает на доске название команды и имя ее капитана.
Второй этап. Дальше, дальше…
Команды получают общее задание, но отвечать будет представитель только одной команды. Каждая команда отвечать будет по очереди, будет 4 задания. Остальные пишут на листах только ответ и сдают лист учителю. На решение каждого задания отводится 3 минуты. На ответ - 1 минута. За каждый верный ответ команда получает “+”, за верное добавление или поправку тоже “+”. Плюсы учитель ставит на доске рядом с названием команды. Минусы не ставятся, просто остается свободное место.
Задание 1: решите уравнение: log 5 (x-1) = log 5 (1-х) + 1,5. Ответ: нет решений (ОДЗ: ? )
Задание 2: обозначим: lg2 = a, lg3 = b. Выразить через a и b: log 5 6. Ответ: (a+b)/(1-a)
(т.к. log 5 6=lg6/lg5=(lg2 + lg3)/(lg10-lg2)=(a+b)/(1-a) )
Задание 3: для каждого значения параметра а решите неравенство относительно х:
logаx < log а 2.
Ответ: если а? 0, а=1, то решений нет; если 0<а<1, то х>2; если а>1, то 0<х<1
Задание 4: приведите пример логарифмического неравенства, которое: а). имеет бесконечное множество решений; б). решением имеет только одно число; в). не имеет решений.
Ответ: например, а). log 3 x < 2; б). log22 x + 4 log 2 х + 4 ? 0; в). log 4 x < log 4 (-х)
Третий этап. Караоке.
Командам одновременно предлагается решить уравнения и про полученное в ответе число напеть строчку из песни, где оно встречается.
1. log 1/2 x = -1 (х=2, “Дважды два – четыре, дважды два – четыре…”)
2. log O 3/3 x = -2 (х=3, “Три танкиста, три веселых друга, экипаж машины боевой…”)
3. lg x = 6 (х=1000000, “Миллион, миллион алых роз…”)
4. log 2 x = -1 (х=0,5, “Половинку сердца оставлю с тобою…”, “Полчаса без тебя, полчаса…”)
5. log 2006 x = 0 (х=1, “Ты единственная моя…”)
Четвертый этап. Найди ошибку.
Команды придумывают задание по теме “Логарифмические уравнения”, в котором содержится ошибка. Задание озвучивается через 2 минуты командой, готовой первой, а первая из команд, которая нашла ошибку, отвечает. Например, a=b ? log 5 a = log 5 b. Ответ: a, b>0
Рефлексия.
В качестве рефлексии всем учащимся предлагается написать синквейн: 3 существительных, которые отвечают внутреннему состоянию учащегося, такие же 3 глагола, 3 прилагательных, 1 слово с “!” на конце и законченное предложение. Учитель собирает листочки.
Подведение итогов.
Учитель делает вывод о степени достижимости поставленных в начале урока целей и благодарит учащихся за работу на уроке.
Домашнее задание: повторить темы: “Логарифмическая функция, ее свойства, графики”, “Преобразование графиков функций”, а также известные высказывания, пословицы и поговорки.
Урок-викторина: “Логарифмическая функция”.Содержание организационного момента и погружения в викторину аналогичны предыдущей викторине, поэтому в рамках данной статьи мы их повторять не будем.
Второй этап. Дальше, дальше…
Команды получают общее задание, но отвечать будет представитель только одной команды. Каждая по очереди, будет 4 задания. Остальные пишут на листах только ответ и сдают лист учителю. На решение каждого задания отводится 3 минуты. На ответ - 1 минута. За каждый верный ответ команда получает “+”, за верное добавление или поправку тоже “+”. Плюсы учитель ставит на доске рядом с названием команды. Минусы не ставятся, просто остается свободное место.
Задание 1: график функции f(x) = log 3
проходит
через начало координат. Какое выражение
находится в? Ответ: х+1
Задание 2: изобразите эскиз графика функции y = log x x. Ответ:
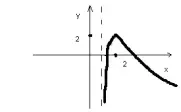
Задание 3: помня, как выглядит график функции f(x) = log 3 x, изобразите эскиз графика функции f(x) = 2 - | log 3 (x-1) | .
(напоминание о преобразованиях графиков: y=f(x)+а
– сдвиг 
на а единиц по ОУ;
у=f(x-а) – сдвиг 
на а единиц по ОХ; у= | f(x) | - часть
графика y=f(x), находящаяся выше ОХ, остается
неизменной, а часть графика y=f(x), находящаяся ниже
ОХ, отображается симметрично относительно ОХ; y= -
f(x) – график y=f(x) отображается симметрично
относительно ОХ). Ответ:
Задание 4: расставьте следующие числа на числовой оси:
log p 7, lg 7, ln 7, 0, 1, log 1/p 7. Ответ:
log 1/p 7 0 lg 7 1 log p 7 ln 7
Третий этап. Творческий.
Командам приводится такой пример: пословицу “Семь бед – один ответ” можно проиллюстрировать таким графиком функции:
Каждой команде предлагается свой график функции. Нужно за 1 минуту предложить пословицу, поговорку, крылатую фразу, которая может быть проиллюстрирована данным графиком, а также из двух предложенных функций выбрать ту, которая соответствует графику.
1).
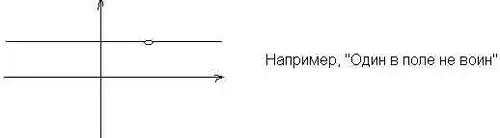
2).
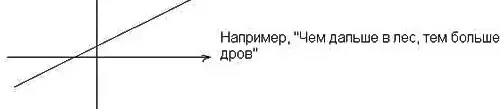
3).
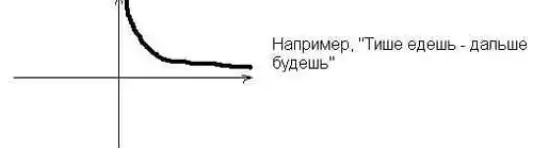
4).
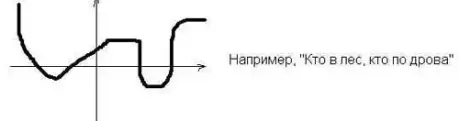
Четвертый этап. Найди ошибку.
Команды придумывают задание по теме “Логарифмическая функция”, в котором содержится ошибка. Задание озвучивается через 2 минуты командой, готовой первой, а первая из команд, которая нашла ошибку, отвечает.
Этапы рефлексии и подведения итогов аналогичны прошлой викторине, поэтому останавливаться на их рассмотрении в рамках данной статьи мы также не будем.
Отметим, что американскими психологами разработана так называемая “пирамида обучаемости”. Согласно ей, после урока, на котором использовалась групповая форма работы, а также практическая работа учащихся, учащимися запоминается до 75% информации.
В заключение статьи приведем примеры двух синквейнов, выполненных учащимися 10 класса экономического профиля школы №22 Санкт-Петербурга, после проведения данных уроков:
1. Выполнил Роман Ф.
2. Выполнила Ольга Е.
